断熱のコツ〜暑い夏を乗り越えろ！〜

こんにちは、ヒラタです。最近暑いので断熱系の話をしたいと思います。

断熱系とは

熱を断つ、と書いて断熱（だんねつ）と読む。我々は外部の影響から隔絶する、すなわち断熱することで系を平衡状態に至らせることができます。

ミクロカノニカルモデル

他にも、いろいろな方法で平衡状態のモデルを作ることが可能ですが、今回は特にこの断熱系モデルについてまとめてみようと思います。

系の状態表記

系というものはいくつかの自由度を持っています。簡単のため、1次元で考えましょう。
例えば、N個の単原子理想気体の自由度は、粒子1つ1つの位置と運動量です。全部で2N個あります。


4つ以上の自由度の様子を2次元平面に図示するのは難しいですが、自由度が十分に大きい場合は分布関数を用いてその様子を表すことができます。

２N個のパラメータの表し方

上の図は、量子力学の確率的な状態によく似ています。しかし、後者が点(x,p)に1粒子が配置されうる確率を表すのに対し、前者は実際に点(x,p)に配置された古典粒子数の分布を表します。ρは規格化条件を満たすとします。

量子力学の詳しい話はコチラ↑

粒子分布ρ(x,p)の安定度を測る道具としてエントロピーがあります。以下の式で表せます。k(>0)はボルツマン定数と呼ばれます。

エントロピーは関数の関数（汎関数）

S(ρ)が大きいほどρは安定的です。なぜ上式のS(ρ)で系の安定度が分かるのでしょうか？？

分布の安定度＝エントロピー

上式を変形するとこうなります。

これは積分変数の変換をしたもので、f(ρ)dρは「分布量幅ρ〜ρ+dρに対応する点(x,ρ)の面積を意味します。（下図の赤い部分の面積）

結局、以下の式に落ち着きます。

エントロピーは-lnρの期待値

さて、ρが規格化条件を満たすことを思い出してください。<1/ρ>の大きさは点(x,p)のある領域の面積と殆ど同じような値だとわかります。（下図）

分布関数を定積変換する

ということは、粒子の状態点(x,p)のバリエーションが多いほど<1/ρ>は大きくなり、エントロピーSも大きくなるということです。

一般に、状態点のバリエーション（状態数）が多い分布ほど安定します。これがエントロピーが系の分布の安定度の基準になる理由です。

※S=klnWを知ってる人は<ρ>=1/W（等重率の原理）によって上の式を得るのもアリです。S=-k<lnρ>は特にギブズエントロピーと呼ばれます。
S1+S2=-k<lnρ1>-k<lnρ2>=-k<ln(ρ1ρ2)>
           =-k<lnρ(1+2)>=S(1+2)
のように示量性も確かめられます。

いよいよ断熱系

準備が整ったので、この記事のテーマである断熱モデルの話をします。引き続き１次元N粒子系でいきます。最初に、各分布ρに対するエントロピーSのグラフを書いてみます。

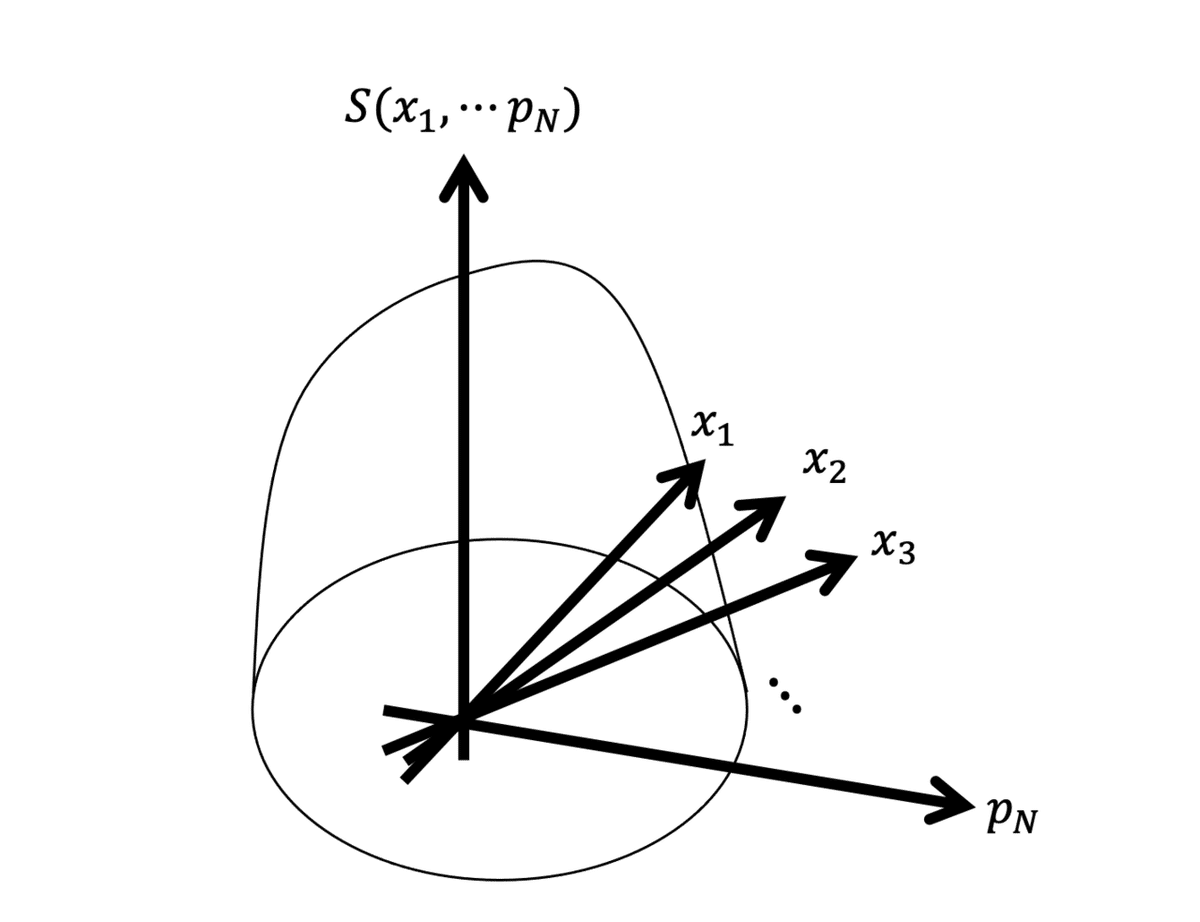
本当は2N次元の関数

曲面（２次元）で書かれてますが、実際の自由度は２N(>>3)個なので、グラフは超曲面になります。

さて、断熱系では系の総エネルギーEが一定値をとります。この条件式「E=一定」はグラフS(ρ)を切断します。（下図）

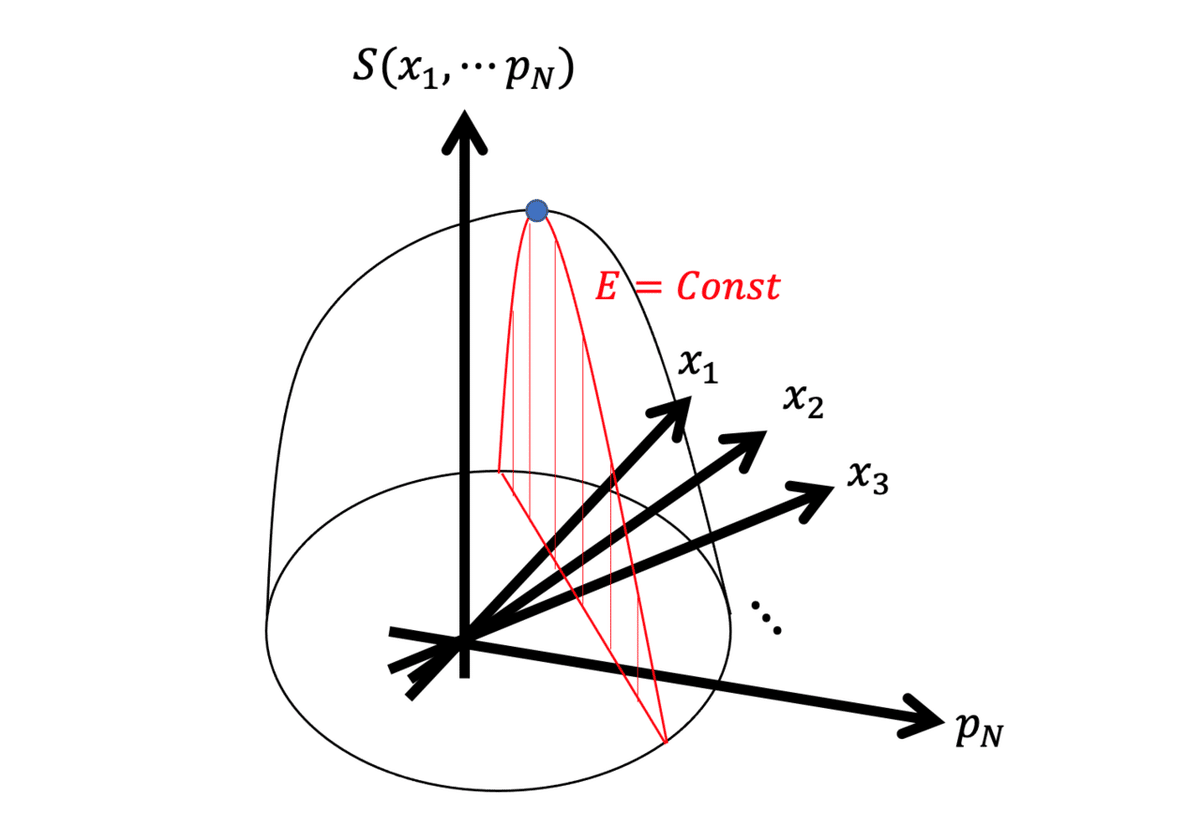
Eもx1〜pNの関数である

このとき、系は赤い部分の分布しかとれません。さらに、十分に時間が経過すると最も安定な分布ρ=ρ*だけをとります（平衡状態）。

ρ*はSが最大になる分布のことで、上図の青い点に対応します。このSの最大値（以下、S*と呼ぶ）はエネルギーEと１対１で対応します。

S(E)というよりS*(E)

平衡状態の性質はグラフS*(E)によって完全に記述できます。系のあらゆる状態量がこのグラフを通して得られるわけです。

※Sはあくまでも自由度分布の関数なので、粒子同士の相互作用の強さ、重力場・電磁場といった情報はもっていないわけです。一方、Eはそういった系の内的情報に詳しい物理量です（自由度の分布にはほぼ無知ですが）
これら２つの関係性を知ることは系の全情報を知ることと同じです。

試しに、グラフS*(E)の導関数（傾き)から得られる情報を考えてみます。
これは「エネルギーずれ⊿Eに対してどれだけの安定性⊿Sが確保できるか」を表す量で、温度と似た性質があります。

傾きdS*/dEの異なる断熱モデルを２つ用意してつなげてみましょう。

つなげるとエネルギーの行き来が可能になる

このとき、系２のエネルギーを系１に移すことで、系全体のエントロピー（安定性）を上げることが出来ます。しかし、ある程度エネルギーが行き来するとdS*/dEが同じ値になります。（下図）

S*1+S*2（全体の安定性）が増やせた

dS*/dEの値が揃うとそれ以上はS*1+S*2を増やせないのでエネルギー伝播は止まります。これは温度が違う系をつなげると温度が揃うまで熱伝導が起こることと対応しています。

しかし、温度が高い方から低い方へエネルギーが伝わるのと違って、dS*/dEが低い方から高い方へエネルギーが伝わります。そのため、dS*/dEは逆温度と呼ばれます。

今回は、S*(E)で平衡状態を表すモデル（断熱モデル）を紹介しました。ルジャンドル変換を使うと、等価なモデルが色々作れたりするのですが長くなるので細かい説明は省略します。

ルジャンドル変換で結ばれるモデル達

おわりに

いかがだったでしょうか。この記事が皆様の断熱の助けになったのでしたら、これに勝る幸せはございません。

物理分野だと、今回の話は熱・統計力学の基礎づけに関連しています。
この分野はプロセス重視の傾向がありますが、基礎がしっかりしているほど道具としての使い勝手も良くなると思います。


8月に入り、熱中症やコロナによる高熱を患う方がますます増えてきています。定期的な断熱を心がけましょう。

それでは、良い夏休みを。