
2-2 散布図の読み取り 〜 散布図の2期間比較
今回の統計トピック
期間の異なる2つの散布図を描いて、データの傾向を読みます!
Pythonでさまざまな種類のグラフ描画を行います。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
2変数記述統計の分野
問2 散布図の読み取り(50歳時未婚率)
試験実施年月
統計検定2級 2019年11月 問2(回答番号3)
問題
公式問題集をご参照ください。
解き方
題意
1つ前の記事の問題と地続きの出題です。
散布図は、横軸が男性の50歳時未婚率(%)、縦軸が女性の50歳時未婚率(%)です。
この問題は「問題文の読解力」と「散布図の読み方」を問う内容になっています。

選択肢①の検討
1990年の女性の値は「1990年の散布図の縦軸」で確認します。
縦軸の 8% で水平線を仮に引いた時、水平線よりも上に位置する点は1つです。
女性で8%を超えている都道府県は1つあります。
選択肢①は適切ではありません。

選択肢②の検討
1990年の男性の値は「1990年の散布図の横軸」で確認します。
横軸の 10% で垂直線を仮に引いた時、垂直線よりも右に位置する点は2つあります。
男性で10%以上の都道府県は2つあります。
選択肢②は適切ではありません。

選択肢③の検討
1990年と2015年の男性の値は「1990年の散布図の横軸」と「2015年の散布図の横軸」で確認します。
1990年の男性の最大値は 10.5% くらいでしょう。
2015年の男性の最小値は 18.2% くらいでしょう。
つまり、2015年の男性の値のすべては1990年よりも高いです。
選択肢③は適切ではありません。

選択肢④の検討
2015年の男性と女性の値は「2015年の散布図の横軸と縦軸」で確認します。
男性の最小値は 18.2% くらいでしょう。
女性の最大値は、一番右上の点を除くと、17.5% くらいでしょう。
一番右上の点以外のケースは、女性の値のすべては男性よりも低いです。
また、一番右上の点は、男性の値が 26% くらい、女性の値が 19% くらいであり、女性の値のほうが低いです。
つまり、2015年のすべての点で女性の値は男性の値よりも低いです。
選択肢④は適切です。

選択肢⑤の検討
2015年の男性と女性の値は「2015年の散布図の横軸と縦軸」で確認します。
女性の値が最も低い点(8.5% くらい)のとき、男性の値は 19.2% くらいです。
男性の値が最も低い点は別にあり(女性の値が 9.2% くらいの点)、その値は 18.2% くらいです。
選択肢⑤は適切ではありません。

解答
④です。
難易度 やさしい
・知識:散布図
・計算力:不要
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
ここでは、2015年と2020年の「都道府県・性別50歳時未婚割合」(単位:%)を参照データとして利用します。
未婚は「まだ結婚したことのない人」のことです。
前回記事「2-1 散布図と度数分布」のデータに2015年を加えました。
【出典記載】
出典:「人口統計資料集(2022年度版)」(国立社会保障・人口問題研究所)(https://www.ipss.go.jp/syoushika/tohkei/Popular/Popular2022.asp?chap=0)
【コンテンツ編集・加工の記載】
記事の記載にあたっては、「人口統計資料集(2022年度版)」(国立社会保障・人口問題研究所)を加工して作成しています。(https://www.ipss.go.jp/syoushika/tohkei/Popular/Popular2022.asp?chap=0)
今回は2期のデータを散布図等で比較します。
散布図
📕公式テキスト:1.6.1 散布図(26ページ~)
散布図はデータの2つの項目ペアをグラフにプロットするものです。
1つ目の項目を横軸( x 軸)、もう1つの項目を縦軸( y 軸)に合わせて、グラフの平面に点を描きます。
散布図の具体的な作成方法については、前回記事「2-1 散布図と度数分布」をご覧ください!
2015年と2020年のデータを比較する
2015年と2020年の情報を1つの散布図にプロットします。
オレンジが 2015年、青が 2020年です。

(参考)1990年~2015年
公式問題集に掲載の「1990年と2015年の25年間」の50歳時未婚率を振り返ります。
この25年間の全体的な傾向は「男性は15ポイントくらい未婚率が高く」なり、「女性は7~10ポイントくらい未婚率が高く」なっている模様です。
2015年~2020年の傾向
では「2015年から2020年の5年間」はどうでしょう。
男性・女性ともに「最も割合の低い都道府県が4ポイントくらい高く」なっています。
50歳時未婚率は年々高まる傾向があるようです。
次のグラフで、横軸に2015年、縦軸に2020年をとり、男性と女性のこの5年間の傾向を見てみます。

右肩上がりの傾向がきれいに出ています。
このことは「すべての都道府県で未婚割合の上昇に一定の傾向が見られる」というふうに、読めそうです。
回帰直線
男性と女性の別に、赤色で回帰直線を引いてみました。
回帰直線は各データ点の傾向に近似する直線です。
この図では「切片=0」にしています。
男女別に回帰直線を見てみましょう。
男性は$${y=1.1424x}$$です。
2020年の割合は2015年の割合の1.14倍(14%)高いようです。
女性は$${y=1.2184x}$$です。
2020年の割合は2015年の割合の1.22倍(22%)高いようです。
世代間の状況
2015年の50歳代は1956年から1965年生まれ。
2020年の50歳代は1961年から1970年生まれ。
5年間の世代の違いと未婚率の違いに、どんな関係があるのでしょう。
それほど遠くない世代ですが、時代背景や文化などの違いがありそうな感じもします。
そして、もっと若い世代が50歳代になるとき、どのような割合になるのでしょう。
未来予想
ちょっぴり未来予想にチャレンジしてみます。
「人口統計資料集(2022年度版)」の1920~2020年の年齢層別未婚割合(全国平均)を見てみましょう。

2020年の50~54歳について、10年前の2010年の40~44歳に青い枠を付けました。
2010年から2020年の間でこの世代層の未婚割合は、男性は 2ポイント、女性は 1ポイントの減少です。
2030年の50~54歳の割合はどのように推移するのでしょう。
赤枠の2020年の40~44歳は、2030年の50~54歳です。
上述の未婚割合の減少の傾向が続くとすると、「?」はどんな数字になるでしょう(30%と20%?)。
将来の世帯の考え方はどうなる?
もしも晩婚化・未婚化が今後も進展を続ける場合には、家族にかかわる法律の仕組み、政府の施策や企業の市場施策を変化させる必要があるかもしれません。
もしかすると、家族のあり方に関する国民の考えが変化するかもしれません。
世界の状況は?
「人口統計資料集(2022年度版)」に主要国の年齢層別未婚割合が載っています。
参考にできる先輩国は見つかるでしょうか。

実践する
散布図を描いてみよう
「都道府県・性別50歳時未婚割合」の参照データは国立社会保障・人口問題研究所のホームページで公開されています。

次のリンクで2022年度版「人口統計資料集」の目次を確認できます。
次のリンクのページでEXCELファイルをダウンロードできます。
「表12-37 都道府県,性別50歳時未婚割合:1920~2020年」です。
男性のページと女性のページが分かれています。
CSVファイルのダウンロード
こちらのリンクから整形後のCSVファイルをダウンロードできます。
2015年と2020年の配偶関係不詳補完結果に基づくデータです。
また、北海道~九州の「七地方区分」を付け加えました。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。
電卓・手作業で作成してみよう!
「知る」の内容をもとにして、散布図を手作業で作成しましょう!
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
データとグラフの関係も実感できると思います。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
2期の散布図の作成
EXCELの散布図グラフを利用します。
完成イメージです。

次の2つの系列データを指定します。
・「2015年の横軸(x軸)=男性、縦軸(y軸)=女性」
・「2020年の横軸(x軸)=男性、縦軸(y軸)=女性」
次の図は「系列の編集」画面で2015年の設定をするイメージです。

もう一つの散布図です。

次の2つの系列データを指定します。
・「男性の横軸(x軸)=2015年、縦軸(y軸)=2020年」
・「女性の横軸(x軸)=2015年、縦軸(y軸)=2020年」
次の図は近似曲線の設定方法を示しています。
グラフの点をダブルクリックすると「近似曲線の書式設定」画面を表示できます。

表示する近似曲線の種類、切片の値、近似曲線の式の表示、決定係数$${R^2}$$の表示などを設定できます。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回はいろんなライブラリの散布図、ヒストグラムを利用して、2015年と2020年の比較に取り組んでみましょう。
①ライブラリのインポート
データ可視化ライブラリseabornを使用します。
回帰直線の作成にscikit-learnのLinearRegressionを使用します。
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。
datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile)
print(df.shape)
display(df.head())
③散布図の表示1(横軸:男性、縦軸:女性)
matplotlibのscatterを利用します。次の3つの散布図を表示します。
2020年 単年 (単純平均付き)
2015年 単年 (単純平均付き)
2015年と2020年
# 単純平均の設定
means = {'2020年_男性': df['2020年_男性'].mean(),
'2020年_女性': df['2020年_女性'].mean(),
'2015年_男性': df['2015年_男性'].mean(),
'2015年_女性': df['2015年_女性'].mean()}
# 共通引数の設定
args_2020 = {'s': 40, 'c': 'lightblue', 'ec': 'darkblue', 'lw':0.7,
'alpha': 0.5, 'label': '2020年'}
args_2015 = {'s': 40, 'c': 'tomato', 'ec': 'red', 'lw':0.7,
'alpha': 0.5, 'label': '2015年'}
args_mean = {'s': 200, 'c': 'yellow', 'ec': 'darkorange',
'marker': '*', 'label': '単純平均'}
fig, ax = plt.subplots(1, 3, figsize=(10, 4), constrained_layout=True,
sharex='all', sharey='all')
# 2020年の散布図のプロット
ax[0].scatter(df['2020年_男性'], df['2020年_女性'], **args_2020)
ax[0].scatter(means['2020年_男性'], means['2020年_女性'], **args_mean)
ax[0].set_title('2020年')
ax[0].set_xlim(0.18, 0.34)
ax[0].set_ylim(0.08, 0.26)
ax[0].set_xticks(np.arange(0.18, 0.34, 0.02))
ax[0].set_yticks(np.arange(0.08, 0.26, 0.02))
ax[0].grid(axis='both', linewidth=0.5, linestyle='--')
ax[0].legend(loc='upper left')
# 2015年の散布図のプロット
ax[1].scatter(df['2015年_男性'], df['2015年_女性'], **args_2015)
ax[1].scatter(means['2015年_男性'], means['2015年_女性'], **args_mean)
ax[1].set_title('2015年')
ax[1].grid(axis='both', linewidth=0.5, linestyle='--')
ax[1].legend(loc='upper left')
# 2015年 + 2020年の散布図のプロット
ax[2].scatter(df['2015年_男性'], df['2015年_女性'], **args_2015)
ax[2].scatter(df['2020年_男性'], df['2020年_女性'], **args_2020)
ax[2].set_title('2015年・2020年')
ax[2].grid(axis='both', linewidth=0.5, linestyle='--')
ax[2].legend(loc='upper left')
fig.supxlabel('男性')
fig.supylabel('女性')
fig.suptitle('散布図:都道府県別50歳時未婚割合')
# plt.savefig('./scatter_all.png') # グラフ画像ファイルの保存
plt.show()
④散布図の表示2(横軸:男性、縦軸:女性)
2015年と2020年を1つの散布図にプロットします。
# 2015年 + 2020年の散布図のプロット
plt.figure(figsize=(5, 5))
plt.scatter(df['2015年_男性'], df['2015年_女性'], **args_2015)
plt.scatter(df['2020年_男性'], df['2020年_女性'], **args_2020)
plt.xlim(0.18, 0.34)
plt.ylim(0.08, 0.26)
plt.xticks(np.arange(0.18, 0.34, 0.02))
plt.yticks(np.arange(0.08, 0.26, 0.02))
plt.grid(axis='both', linewidth=0.5, linestyle='--')
plt.title('散布図:都道府県別50歳時未婚割合')
plt.xlabel('男性')
plt.ylabel('女性')
plt.legend(loc='upper left')
# plt.savefig('./scatter_2015-2022.png') # グラフ画像ファイルの保存
plt.show()
⑤ヒストグラムの表示
matplotlibのhistを利用してヒストグラムを表示します。
# histの共通引数の設定
args_hist = {'bins': 13, 'range': (0.08, 0.34), 'ec': 'white'}
fig, ax = plt.subplots(2, 2, figsize=(6, 5), constrained_layout=True,
sharex='all', sharey='all')
# 2015年・男性のヒストグラムのプロット
ax[0][0].hist(df['2015年_男性'], **args_hist)
ax[0][0].set_title('2015年 男性', fontsize=10)
ax[0][0].set_xticks(np.arange(0.08, 0.34, 0.04))
# 2020年・男性のヒストグラムのプロット
ax[0][1].hist(df['2020年_男性'], **args_hist)
ax[0][1].set_title('2020年 男性', fontsize=10)
# 2015年・女性のヒストグラムのプロット
ax[1][0].hist(df['2015年_女性'], **args_hist)
ax[1][0].set_title('2015年 女性', fontsize=10)
# 2020年・女性のヒストグラムのプロット
ax[1][1].hist(df['2020年_女性'], **args_hist)
ax[1][1].set_title('2020年 女性', fontsize=10)
fig.supxlabel('割合')
fig.supylabel('都道府県数(度数)')
fig.suptitle('ヒストグラム:都道府県別50歳時未婚割合')
# plt.savefig('./hist_all.png') # グラフ画像ファイルの保存
plt.show()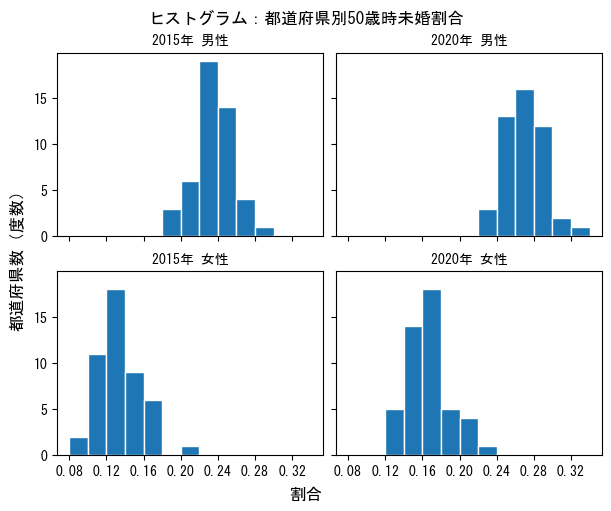
⑥ジョイントプロットの表示1(横軸:男性、縦軸:女性)
seabornのjointplotを利用して、散布図とヒストグラムの両方を表示します。jointplotの引数kind='reg'を指定して回帰直線等を表示しています。
引数kind='scatter'を指定すると、散布図とヒストグラムだけの表示になります。
# 散布図とヒストグラムのジョイントプロットを作成 2020年
sns.jointplot(data=df, x='2020年_男性', y='2020年_女性', kind='reg',
height=5, ratio=2, marginal_ticks=True, color='steelblue')
plt.suptitle('ジョイントプロット:都道府県別50歳時未婚割合(2020年)')
plt.tight_layout()
# plt.savefig('./jointplot_2020.png') # グラフ画像ファイルの保存
plt.show()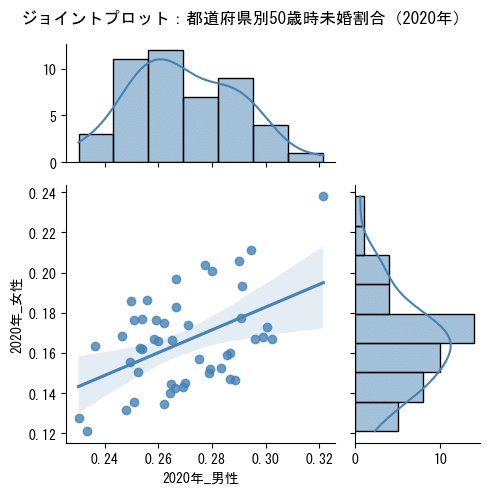
# 散布図とヒストグラムのジョイントプロットを作成 2015年
sns.jointplot(data=df, x='2015年_男性', y='2015年_女性', kind='reg',
height=5, ratio=2, marginal_ticks=True, color='tomato')
plt.suptitle('ジョイントプロット:都道府県別50歳時未婚割合(2015年)')
plt.tight_layout()
# plt.savefig('./jointplot_2015.png') # グラフ画像ファイルの保存
plt.show()
⑦散布図の表示3(横軸:2015年、縦軸:2020年)
男性・女性の別に回帰直線とその式・決定係数を表示します。
・最初のコードで 線形回帰のインスタンスを生成します。
・reg.fit(x, y)で回帰モデルの学習を行い、回帰係数(reg.coef_)と切片(reg.intercept_)を算出します。
・reg.score(x, y)で決定係数$${R^2}$$を算出します。
・y_pred_men = reg.predict(x)で散布図にプロットする回帰直線のyの値を取得します。
# 回帰係数等の算出
reg = LinearRegression()
# 男性
x = pd.DataFrame(df['2015年_男性'])
y = pd.DataFrame(df['2020年_男性'])
reg.fit(x, y)
r2_men, coef_men, intercept_men = reg.score(x, y), reg.coef_, reg.intercept_
y_pred_men = reg.predict(x)
# 女性
x = pd.DataFrame(df['2015年_女性'])
y = pd.DataFrame(df['2020年_女性'])
reg.fit(x, y)
r2_women, coef_women, intercept_women = reg.score(x, y), reg.coef_, reg.intercept_
y_pred_women = reg.predict(x)
# scatter引数の設定
args_men = {'s': 40, 'c': 'lightblue', 'ec': 'darkblue', 'lw':0.7,
'alpha': 0.5, 'label': '男性'}
args_women = {'s': 40, 'c': 'tomato', 'ec': 'red', 'lw':0.7,
'alpha': 0.5, 'label': '女性'}
plt.figure(figsize=(5, 5))
# 散布図のプロット
plt.scatter(df['2015年_男性'], df['2020年_男性'], **args_men)
plt.scatter(df['2015年_女性'], df['2020年_女性'], **args_women)
# 回帰直線のプロット
plt.plot(df['2015年_男性'], y_pred_men, c='navy', lw=1)
plt.plot(df['2015年_女性'], y_pred_women, c='red', lw=1)
# 修飾
plt.xlim(0.08, 0.32)
plt.ylim(0.10, 0.34)
plt.xticks(np.arange(0.08, 0.32, 0.02))
plt.yticks(np.arange(0.10, 0.34, 0.02))
plt.grid(axis='both', linewidth=0.5, linestyle='--')
plt.title('散布図:都道府県別50歳時未婚割合')
plt.xlabel('2015年')
plt.ylabel('2020年')
# 回帰直線の式と決定係数の表示
plt.text(0.20, 0.32, f'$y = {coef_men[0][0]:.3f}x + {intercept_men[0]:.3f}$')
plt.text(0.20, 0.305, f'$R^2 = {r2_men:.3f}$')
plt.text(0.13, 0.14, f'$y = {coef_women[0][0]:.3f}x + {intercept_women[0]:.3f}$')
plt.text(0.13, 0.125, f'$R^2 = {r2_women:.3f}$')
plt.legend(loc='upper left')
# plt.savefig('./scatter_men-women.png') # グラフ画像ファイルの保存
plt.show()
⑧ジョイントプロットの表示2(横軸:2015年、縦軸:2020年)
# 散布図とヒストグラムのジョイントプロットを作成 男性
sns.jointplot(data=df, x='2015年_男性', y='2020年_男性', kind='reg',
height=5, ratio=2, marginal_ticks=True, color='steelblue')
plt.suptitle('ジョイントプロット:都道府県別50歳時未婚割合(男性)')
plt.tight_layout()
# plt.savefig('./jointplot_men.png') # グラフ画像ファイルの保存
plt.show()
# 散布図とヒストグラムのジョイントプロットを作成 女性
sns.jointplot(data=df, x='2015年_女性', y='2020年_女性', kind='reg',
height=5, ratio=2, marginal_ticks=True, color='tomato')
plt.suptitle('ジョイントプロット:都道府県別50歳時未婚割合(女性)')
plt.tight_layout()
# plt.savefig('./jointplot_women.png') # グラフ画像ファイルの保存
plt.show()
⑨ペアプロットの表示
seabornのpairplotを利用して、ヒストグラムと散布図をデータ項目のマトリクスの形式で表示します。
# ヒストグラムと散布図のペアプロットを表示
sns.pairplot(df, height=1.5, aspect=1)
plt.suptitle('ペアプロット:都道府県別50歳時未婚割合')
plt.tight_layout()
# plt.savefig('./pairplot_all.png') # グラフ画像ファイルの保存
plt.show()
おまけ:地方属性を加味したペアプロット
seaborn.pairplotの引数hue='地方'を指定して、地方属性ごとに色分けして描画できます。
# ヒストグラムと散布図のペアプロットを表示
sns.pairplot(df, hue='地方', diag_kind='hist', height=1.5, aspect=1)
plt.suptitle('ペアプロット:都道府県別50歳時未婚割合', x=0.5, y=1.03)
# plt.savefig('./pairplot_all_hue.png') # グラフ画像ファイルの保存
plt.show()
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
「のんびり統計」の記事を書く習慣とともに、EXCELとPythonのグラフ描画が楽しくなりました。
ひとまずやってみること、そして積み重ねることの大切さをしみじみと実感しています。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
