
時系列分析入門【第4章 その5】変化点モデル・隠れマルコフモデルの状態空間モデルをPythonとPyMC Ver.5 で実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第4章「RStanによる状態空間モデル」のRスクリプト・Stanコードをお借りして、PythonとPyMC Ver.5 で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは「状態(パラメータ)が離散的」である状態空間モデルです。
・変化点モデル
・隠れマルコフモデル
今回はPyMCでモデリングします。
まぁまぁ、諸々はさておいて、時系列分析とベイズモデリングを楽しんでいきましょう!
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第4章 RStanによる状態空間モデル
この記事は「4.4 状態が離散的であるモデル」を実践いたします。
インポート(+環境準備)
この記事で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# グラフ描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】PyMC環境の構築
AnacondaでPyMC環境を構築する方法を次のリンクの「pymc環境の構築」の箇所に記載しています。
ご参考まで。

テキストが「状態が離散的であるモデル」を論点にするのは「Stanが離散パラメータを扱えない」という事情があるからのようです。
PyMCは離散パラメータを扱えるので、離散だからといって特に問題はありません。
ただし、モデル自体が難しい場合は、(私的に)問題があります(汗)
変化点モデル
テキストによると、変化点検出は、時系列データに離散的な変化が表れた箇所を見つけ出す方法の総称だそうです。
テキストのデータ&モデルを用いて、変化点$${cp}$$(変化する日)が訪れた後に効果$${diff}$$が加算されるモデルを検討します。
モデルの数式です。
$$
\begin{align*}
\delta_t &= \begin{cases} diff & (cp \leq t) \\0 & (\text{otherwise})\end{cases} \\
\mu_t &\sim \text{Normal}\ (\mu_{t-1},\ \sigma^2_{w}) \\
Y_t &\sim \text{Normal}\ (\mu_t + \delta_t,\ \sigma^2_o) \\
\end{align*}
$$
① データの作成・前処理
テキストのRコードを参考にしてデータ作成します。
50日の時点で介入$${a=3}$$を平均パラメータに加算して正規分布乱数を生成します。
なお、生成する乱数がテキストと異なるため、出来上がったデータ&ベイズ推論結果もテキストと異なる結果になることを予めご了承くださいませ。
### データの準備 # Rコードより
# 初期値設定
np.random.seed(1)
N = 100 # 期間
cp = 50 # 変化点
mu_0 = 0 # 状態muの初期値
sigma_W = 0.1 # システムノイズの標準偏差
sigma_O = 0.1 # 観測ノイズの標準偏差
a = 3 # 介入効果の大きさ
# 状態の初期値
mu, y = np.zeros(N), np.zeros(N)
mu[0] = mu_0
## データの生成
# 状態:mu
for i in range(1, N):
if i==cp-1:
mu[i] = np.random.normal(loc=mu[i-1]+a, scale=sigma_W, size=1)
else:
mu[i] = np.random.normal(loc=mu[i-1], scale=sigma_W, size=1)
# 観測値:y
y = np.random.normal(loc=mu, scale=sigma_O)
# データフレーム化
df_cp = pd.DataFrame({'Time': range(1, N+1), 'y': y})
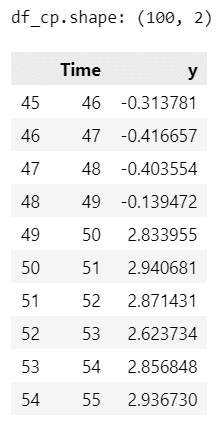
print('df_cp.shape:', df_cp.shape)
display(df_cp.iloc[45:55])【実行結果】
100日分のデータです。
Time=50以降、目的変数 y の値がぐんと大きくなります。
テキストにならって、データを描画します。
テキストの図4.20に相当します。
### 描画 ★図4.20に相当
plt.figure(figsize=(12, 4))
plt.plot(df_cp['Time'], df_cp['y'])
plt.axvline(50, color='black', lw=0.5, ls='--')
plt.xlabel('Time')
plt.ylabel('y');【実行結果】
50日にグンとUPしています⤴

② モデルの定義
テキストのモデルに類似する内容でモデルを定義しました。
システムモデル(レベル成分)の記述には「pm.GaussianRandomWalk()」を利用しました。
時系列分析感が出てきますね!
### モデルの定義
with pm.Model() as model_cp1:
### データ関連定義
# coordの定義
model_cp1.add_coord('data', values=df_cp.index, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=df_cp['y'].values, dims='data')
t = pm.ConstantData('t', value=df_cp['Time'], dims='data')
### 事前分布
sigmaW = pm.HalfCauchy('sigmaW', beta=5)
sigmaO = pm.HalfCauchy('sigmaO', beta=5)
cp = pm.Uniform('cp', lower=1, upper=N)
diff = pm.Uniform('diff', lower=-100, upper=100)
# mu:レベル成分
init_dist_mu = pm.Normal.dist(mu=0, sigma=100)
mu = pm.GaussianRandomWalk('mu', mu=0, sigma=sigmaW, init_dist=init_dist_mu,
dims='data')
# delta:変化点で加わる効果
delta = pm.Deterministic('delta', pt.switch(pt.le(cp, t), diff, 0),
dims='data')
### 尤度:観測モデル
likelihood = pm.Normal('likelihood', mu=mu+delta, sigma=sigmaO, observed=y,
dims='data')【実行結果】出力なし
③ モデルの表示・可視化
モデルの数式を表示します。
### モデルの表示
model_cp1【実行結果】

モデルを図にして可視化しましょう。
# モデルの可視化
pm.model_to_graphviz(model_cp1)【実行結果】
変化点$${cp}$$と変化後の加算値$${diff}$$が$${delta}$$と関連します。

④ 事後分布からのサンプリング
MCMCを実行します。
NUTSサンプラーにnumpyroを利用します。
実行時間はおよそ50秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 50秒
with model_cp1:
idata_cp1 = pm.sample(draws=6000, tune=2000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果(一部)】

⑤ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_cp1 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum().data_vars)【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
pm.summary(idata_cp1, hdi_prob=0.95, var_names=['cp', 'diff', 'sigmaO', 'sigmaW'])【実行結果】
変化点$${cp}$$は平均値$${49.50}$$、95%HDI区間が$${[49,\ 49.95]}$$です。
ほぼ50です

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_cp1, combined=True, figsize=(10, 15))
plt.tight_layout();【実行結果】
収束している感じがします。
発散を示すバーコードが多いですね(汗)

⑥ $${\boldsymbol{cp}}$$の描画
テキストの図4.21に相当する図を描画します。
描画にplot_posterior()を利用します。
### 効果が現れるまでの日数の事後分布 ※図4.21に相当
pm.plot_posterior(idata_cp1, var_names=['cp'], hdi_prob=0.95);【実行結果】
ざっくり50!


アディショナルタイムです!
パラメータに離散値を用いたモデルを試してみましょう!
ガウスランダムウォークや自己回帰モデルを使わないでモデリングできます。
もはや状態空間モデルでは無くなっています。
■モデルの定義
変化点$${cp}$$が整数値をとる離散一様分布 pm.DiscreteUniform に従うモデルです。
変化点前の平均$${\lambda_1}$$と変化点後の平均$${\lambda_2}$$が指数分布に従うものと仮定しています。
### モデルの定義
# 指数分布のパラメータの算出 平均の逆数
alpha = 1 / df_cp['y'].mean()
# モデルの定義
with pm.Model() as model_cp2:
### データ関連定義
# coordの定義
model_cp2.add_coord('data', values=df_cp.index, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=df_cp['y'].values, dims='data')
t = pm.ConstantData('t', value=df_cp['Time'], dims='data')
### 事前分布
sigmaO = pm.HalfCauchy('sigmaO', beta=5)
cp = pm.DiscreteUniform('cp', lower=1, upper=N)
lam1 = pm.Exponential('lam1', lam=alpha) # cp前の平均値
lam2 = pm.Exponential('lam2', lam=alpha) # cp以後の平均値
# 平均λの計算
lam = pm.Deterministic('lam', pt.switch(pt.gt(cp, t), lam1, lam2),
dims='data')
### 尤度:観測モデル
likelihood = pm.Normal('likelihood', mu=lam, sigma=sigmaO, observed=y,
dims='data')■モデルの表示・可視化
### モデルの表示
model_cp2【実行結果】

# モデルの可視化
pm.model_to_graphviz(model_cp2)描画します。

■事後分布からのサンプリング
PyMC標準のサンプラーを利用して、およそ2分15秒かかりました。
### 事後分布からのサンプリング 2分15秒
with model_cp2:
idata_cp2 = pm.sample(draws=6000, tune=2000, chains=4, target_accept=0.8,
random_seed=1234)【実行結果】

■サンプリングデータの確認
$${\hat{R} \leq 1.1}$$であり、収束しています。
### r_hat>1.1の確認
# 設定
idata_in = idata_cp2 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum().data_vars)【実行結果】

要約統計情報を表示します。
### 推論データの要約統計情報の表示
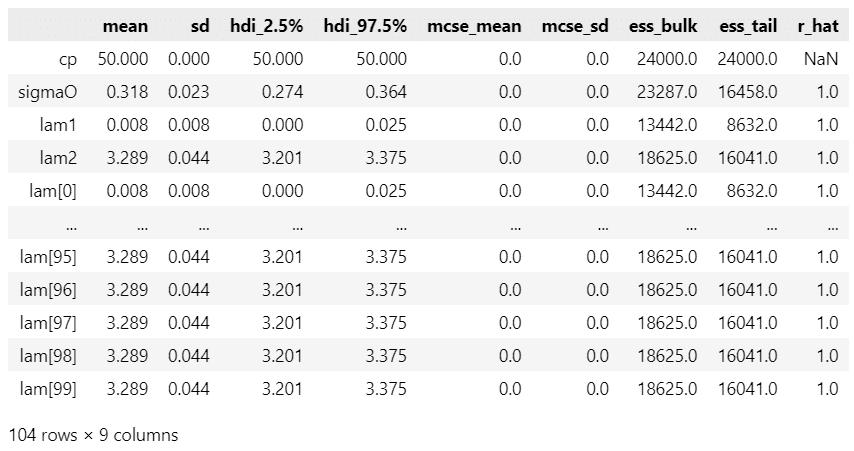
pm.summary(idata_cp2, hdi_prob=0.95)【実行結果】
変化点$${cp}$$は$${50}$$です。
トレースプロットを描画します。
### トレースプロットの表示
pm.plot_trace(idata_cp2, combined=True, figsize=(10, 8))
plt.tight_layout();【実行結果】

■テキストの図4.21に相当する変化点$${cp}$$の事後分布の描画
### 効果が現れるまでの日数の事後分布 ※図4.21に相当
pm.plot_posterior(idata_cp2, var_names=['cp'], hdi_prob=0.95);【実行結果】
平均値も95%HDIの両端も50です!
ぬりかべのような推測値です!


隠れマルコフモデル
テキストによるレジームと隠れマルコフモデルの説明を要約します。
状態が離散的に変化するモデルを「レジームスイッチングモデル」と呼ぶ
レジームがマルコフ連鎖(離散型の確率過程)に従うモデルを「マルコフ転換モデル」と呼ぶ
音声認識で用いられる隠れマルコフモデル(Hidden Markov Model:HMM)はマルコフ転換モデルの一種である。
複数のレジームがある確率~遷移確率行列~に従って、つまり、1期前のレジームの遷移確率(各レジームに遷移する確率、合計1)に従って、今期のレジームが決まるモデルです。
詳しくはテキストの図4.22を参照してください。
遷移確率行列のイメージです。

① データの作成・前処理
テキストのRコードを参考にしてデータ作成しました。
【おことわり】
生成する乱数の相違から、この記事で利用するデータはテキストと異なります。
したがいまして、推論結果もテキストと相違することを予めお断りいたします。
### データの準備 # Rコードより
## 初期値設定
# 設定値
N = 50 # 期間
np.random.seed(62) # 62
# 遷移確率
P = np.array([[0.8, 0.1, 0.1],
[0.1, 0.8, 0.1],
[0.2, 0.2, 0.6]])
# レジームごとの潜在変数の値
mu = np.array([0, 5.0, 10.0])
# レジームごとの観測ノイズ
sigma = np.array([1.0, 1.0, 1.0])
# 仮想データの作成
y, z = np.zeros(N), np.zeros(N).astype('int')
z[0] = np.random.choice([1, 2, 3], size=1, replace=True, p=[1/3, 1/3, 1/3])
for i in range(1, N):
z[i] = np.random.choice([1, 2, 3], size=1, replace=True, p=P[z[i-1]-1])
# 観測ノイズを加えて観測値を生成
y = np.random.normal(loc=mu[z-1], scale=sigma[z-1])
# データフレーム化
df_hm = pd.DataFrame({'Time': range(1, N+1), 'y': y, 'Regime': z})
df_hm['mu'] = df_hm['Regime'].apply(lambda x: mu[x-1])
print('df_hm.shape:', df_hm.shape)
display(df_hm.head())【実行結果】
50期分のデータです。
以下は項目内容です。
・Time:時間(期)
・y:目的変数
・Regime:レジーム1~3
・mu:レジームに対応するmuの値。1:0、2:5、3:10

テキストにならって、データを描画します。
テキストの図4.23に相当します。
matplotlibのtwinx()を用いて、左右に y軸目盛りを設定しています。
### 描画 ※図4.23に相当
fig, ax1 = plt.subplots(figsize=(10, 4))
# 1つの描画領域にax1とax2のy軸を表示
ax2 = ax1.twinx()
# yの描画
ax1.plot(df_hm['Time'], df_hm['y'], label='Y')
# regimeの描画
ax2.scatter(df_hm['Time'], df_hm['Regime'], edgecolor='tomato', facecolor='none',
s=50, label='Regime')
# 凡例を1つにまとめる
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1+h2, l1+l2)
# 修飾
ax1.set(xlabel='Time', ylabel='Y')
ax2.set(yticks=(1, 2, 3), ylabel='Regime')
plt.show()【実行結果】
レジームの遷移に沿って観測値 y (誤差を含む)が移動しているように見えます。

② モデルの定義
個人的にかなり難易度が高いモデリングでした。
なお、テキストでレジーム推定に用いている「ビタビ・アルゴリズム」は実装していません。実装方法が分からないからです(汗)
さあ、最適化ロジックを廃したモデルの結末はいかに???
### モデルの定義
### 初期値設定
# 状態の数
k = 3
# ディリクレ分布・カテゴリカル分布のパラメータ
init_param = np.ones(k) / k
### モデルの定義
with pm.Model() as model_hm1:
### データ関連定義
# coordの定義
model_hm1.add_coord('data', values=df_hm.index, mutable=True)
model_hm1.add_coord('regime', values=range(1, k+1), mutable=True)
# dataの定義
y = pm.ConstantData('y', value=df_hm['y'].values, dims='data')
### 事前分布
# 遷移確率theta
theta = pm.Dirichlet('theta', a=init_param, shape=(k, k))
# 状態(レジューム):state
state = [0] * N
state[0] = pm.Categorical('state0', p=init_param)
for t in range(1, N):
state[t] = pm.Categorical(
'state' + str(t),
p=pt.switch(pt.eq(state[t-1], 0), theta[0],
pt.switch(pt.eq(state[t-1], 1), theta[1], theta[2]))
)
# 潜在変数:mu
# ラベルスイッチを防止して、mu0 <= mu1 <= mu2となるよう、delta0,1を利用
mu0 = pm.Normal('mu0', mu=0, sigma=100)
delta0 = pm.HalfNormal('delta0', sigma=100)
delta1 = pm.HalfNormal('delta1', sigma=100)
mu1 = pm.Deterministic('mu1', mu0 + delta0)
mu2 = pm.Deterministic('mu2', mu1 + delta1)
mus = pm.Deterministic('mus', pt.stack([mu0, mu1, mu2]), dims='regime')
mu = pm.Deterministic('mu',
pt.switch(pt.eq(state, 0), mus[0],
pt.switch(pt.eq(state, 1), mus[1], mus[2])),
dims='data')
# 観測モデルの標準偏差
sigmaOs = pm.HalfCauchy('sigmaOs', beta=5, dims='regime')
sigmaO = pm.Deterministic('sigmaO',
pt.switch(pt.eq(state, 0), sigmaOs[0],
pt.switch(pt.eq(state, 1), sigmaOs[1], sigmaOs[2])),
dims='data')
### 尤度:観測モデル
likelihood = pm.Normal('likelihood', mu=mu, sigma=sigmaO, observed=y,
dims='data')【実行結果】出力なし
【補足】
レジーム(状態)を表す state は離散型分布であるカテゴリカル分布「pm.Categorical」に従います。
確率引数 p には、1期前のレジームの状態に基づく遷移確率を用います。
### 1番目のstateの例
state[0] = pm.Categorical('state0', p=init_param)遷移確率 theta は3×3の行列です。
1行の確率の合計が1になるようにディリクレ分布 pm.Dirichlet を用いています。
theta = pm.Dirichlet('theta', a=init_param, shape=(k, k))MCMC実行時にchain(連鎖)を複数利用する目的で、$${\mu_0 \leq \mu_1 \leq \mu_2}$$を維持できるようにラベルスイッチを防止する措置を実装しました。
0以上の値を持つ delta0 と delta1 を設けて、mu1 = mu0 + delta0、mu2 = mu1 + delta1 の関係性を作りました。
mu0 = pm.Normal('mu0', mu=0, sigma=100)
delta0 = pm.HalfNormal('delta0', sigma=100)
delta1 = pm.HalfNormal('delta1', sigma=100)
mu1 = pm.Deterministic('mu1', mu0 + delta0)
mu2 = pm.Deterministic('mu2', mu1 + delta1)
mus = pm.Deterministic('mus', pt.stack([mu0, mu1, mu2]), dims='regime')ラベルスイッチ回避策の知見は次の書籍から得ました。
ありがとうございます!
③ モデルの表示・可視化
モデルの数式を表示します。
# モデルの表示
model_hm1【実行結果】
一部途切れています。
stats を 50期分持つので、とても長い図になりそうです。

モデルを図にして可視化しましょう。
# モデルの可視化
pm.model_to_graphviz(model_hm1)【実行結果】
なんじゃこりゃー!ですね。

④ 事後分布からのサンプリング
MCMCを実行します。
収束悪化防止の目的で、target_accept=0.998 としました。
PyMC標準のサンプラーを用いて、およそ55分かかりました。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを未使用 53分
with model_hm1:
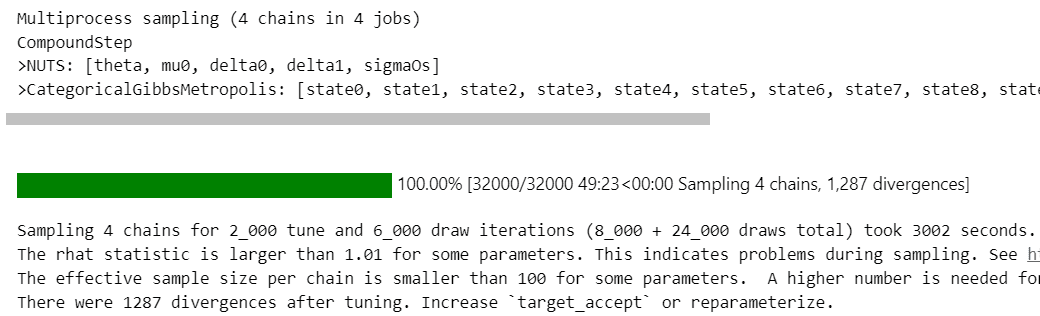
idata_hm1 = pm.sample(draws=6000, tune=2000, chains=4, target_accept=0.998,
random_seed=1234)【実行結果(一部)】
⑤ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_hm1 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum().data_vars)【実行結果】
$${\hat{R}>1.1}$$のパラメータが多数存在します。
収束できなかったようです(泣)
これにて分析は断念いたします(泣)

パラメータ等の事後分布の要約統計量です。
まずはレジーム(状態)です。
### 推論データの要約統計情報の表示
pm.summary(idata_hm1, hdi_prob=0.95, var_names=['state'], filter_vars='like')【実行結果】

続いて3つのパラメータです。
### 推論データの要約統計情報の表示
var_names = ['sigmaO', 'theta', 'mu']
pm.summary(idata_hm1, hdi_prob=0.95, var_names=var_names)【実行結果】
データ生成時のパラメータ値と比べて、sigmaに対応するsigmaOs、muに対応するmusの両方がぜんぜん違う値になりました(汗)

(参考:データ生成時のパラメータ値)

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_hm1, combined=True, var_names=var_names, filter_vars='like',
figsize=(10, 10))
plt.tight_layout();【実行結果】
右側の裾が長い分布になりました。
発散も多いです。

一応、状態変化の推定値を見ておきましょう。
テキストの図4.24に相当します。
### 状態変化の推定の描画 ※図4.24に相当
## ベイズ推論した状態0~49のレジーム平均値を算出
# pm.summary()でstateの平均値を算出
state_means = pm.summary(idata_hm1, hdi_prob=0.95, var_names=['state'],
filter_vars='like')
# 平均値を四捨五入で整数に丸め
state_means = state_means['mean'].round(0) + 1
## 描画
fig, ax = plt.subplots(figsize=(10, 4))
# 1つの描画領域にax1とax2のy軸を表示
# regimeの描画
ax.plot(df_hm['Time'], df_hm['Regime'], color='tab:blue', label='Regime')
# ベイズ推論したregimeの平均値の描画
ax.plot(df_hm['Time'], state_means, color='tomato', ls='--',
label='Bayse Regime')
# 修飾
ax.set(xlabel='Time', yticks=(1, 2, 3), ylabel='Regime')
ax.legend()
plt.show()【実行結果】
青い線が生成データのレジーム遷移(真のレジーム)、赤い点線がベイズ推論したレジーム推移です。
なんと!ほぼ一致しました。奇跡です、ベイズマジック。

以上で終了です。
お疲れ様でした。

まとめ
離散値のパラメータを扱う「変化点モデル」と「隠れマルコフモデル」に取り組みました。
PyMCは離散パラメータを扱えるので、パラメータの事前分布に離散型分布を利用したモデルを試してみました。
変化点モデルでは変化点$${cp}$$を推定できました。
隠れマルコフモデルでは、分布が収束しませんでした(泣)

(参考)推論データ(idata)の保存コード
pickle形式で保存します。
### idataの保存 pickle
# ユーティリティ
import pickle
file = r'ch04_05_idata_cp1.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_cp1, f)
file = r'ch04_05_idata_cp2.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_cp2, f)
file = r'ch04_05_idata_hm1.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_hm1, f)読み込みコードは次のとおりです。
「file」のパス&ファイル名と「idata_cp1_load」を適宜変更してお使い下さい。
### idataの読み込み(例)
file = r'ch04_05_idata_cp1.pkl'
with open(file, 'rb') as f:
idata_cp1_load = pickle.load(f)第4章 その6 へ続く
■次回の取り組みテーマ
モデル選択のテーマで「WAIC」と「時系列分割による交差検証」を行います。
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
