
時系列分析入門【第2章 前編】時系列分析のR基本操作をPythonで実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第2章「時系列分析の基本操作」のRスクリプトをお借りして、Pythonで「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは次の基本操作です。
・日付・時刻・日付インデックスの操作
・ラグ、階差、移動平均、移動相関の算出
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第2章 時系列分析の基本操作
インポート
この章で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# 日付
from datetime import time, date, datetime
from dateutil import tz
# Rデータセット・一般化線形モデル・時系列分析
import statsmodels.api as sm
from statsmodels.tsa.seasonal import seasonal_decompose, STL
from statsmodels.graphics.tsaplots import plot_acf
# Googleトレンドアクセス
from pytrends.request import TrendReq
# ARIMAモデル自動選択
import pmdarima as pm
# グラフ描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】パッケージのインストール
利用環境に応じてパッケージをインストールしてください。
以下はインストールの参考コードです。
### インストール
## pytrends
# anaconda
conda install -c conda-forge pytrends
# pip
pip install pytrends
## pmdarima
# anaconda
conda install -c conda-forge pmdarima
# pip
pip install pmdarima2.3.1 日付や時刻を扱うクラス
この節はRの日付関連クラスによる日付・時刻の基本操作を扱っています。
この記事では、python標準ライブラリのdatetimeに加えて、pandasの日付インデックスに焦点を当てて、日付関連処理のコード例を検討します。
なお、テキストの日付例をそのまま使わず、別の日付に変えています。
① datetimeライブラリのdateクラスを用いた日付処理
今日の日付、2012年6月10日の日付、2つの日付の差分計算を行います。
### datetimeのdateクラスを用いた日付処理
# 今日の日付を設定
today = date.today()
print(today)
# 2012年6月10日を設定
d = date(2012, 6, 10)
print(d)
# 日付の差分を計算
print(today - d)【実行結果】
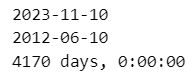
② 文字列を日付に変換
datetimeのdatetimeクラスのstrptimeを利用して、文字列データを日付に変換します。
第1引数に文字列、第2引数に日付フォーマットを指定します。
### 文字列を日付に変換 datetimeのdatetimeクラスのstrptimeを利用
print(datetime.strptime('2023年11月15日', '%Y年%m月%d日'))
print(datetime.strptime('23ねん11がつ15にち', '%yねん%mがつ%dにち'))
print(datetime.strptime('November 15, 2023', '%B %d, %Y'))
print(datetime.strptime('15 Nov, 2023', '%d %b, %Y'))
print(datetime.strptime('15/11/2023', '%d/%m/%Y'))【実行結果】
すべて同じ日付です。

③ 日付を文字列に変換
datetimeのdateクラスのstrftimeを利用して、日付データを文字列に変換します。
変数dに設定した2023年11月15日の日付をテキストのフォーマットを用いて文字列に変換します。
### 日付を文字列に変換 datetimeのdateクラスのstrftimeを利用
d = date(2023, 11, 15)
print(d.strftime('%Y年%m月%d日'))
print(d.strftime('%yねん%mがつ%dにち'))
print(d.strftime('%B %d, %Y'))
print(d.strftime('%d %b, %Y'))
print(d.strftime('%d/%m/%Y'))【実行結果】
いろんな文字列表現ができました。

④ 日付を用いた作図
x軸に日付を用いた折れ線グラフをmatplotlibで描画します。
テキストの図2.5に相当します。
### 日付を用いた作図 datetimeのdateクラスを利用 ※図2.5に相当
x = [date(2022, 4, 11), date(2022, 10, 11), date(2023, 4, 11)]
y = [5, 2, 3]
plt.figure(figsize=(6, 3))
plt.plot(x, y)
plt.xlabel('Day')
plt.ylabel('Value')
plt.show()【実行結果】
x軸の軸ラベルが「年月」になっています。
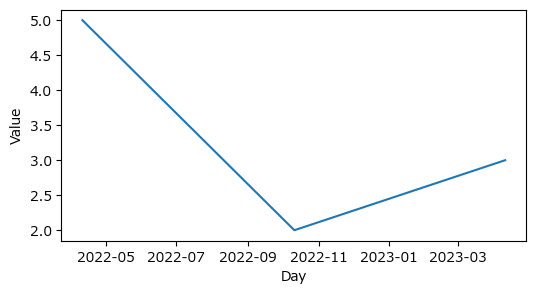
⑤ 連続する日付データの作成
pandasのdate_rangeインデックスを利用して、連続する日付を算出します。
### 連続する日付データの作成 pandasのdate_rangeインデックスを利用
pd.date_range(start='2020-12-25', end='2021-01-10', freq='D')【実行結果】
2020年12月25日から2021年1月10日までの毎日の日付を取得できました。

pandasの日付インデックスは「.values」でnumpyのndarrayに変換できます。
データの型はnumpyのdatetime64になるようです。
date_data = pd.date_range(start='2020-12-25', end='2021-01-10', freq='D').values
date_data【実行結果】
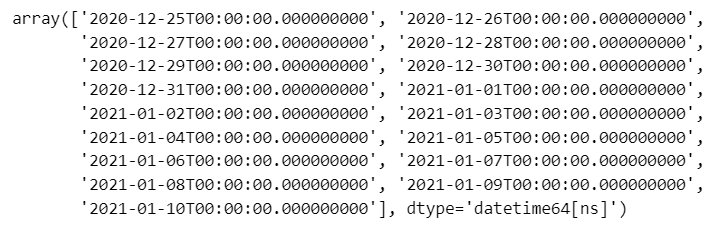
⑥ 日付にタイムゾーンを設定
タイムゾーン・サマータイムの扱いは複雑です。
日常使わないため、理解しにくい概念です。
この記事では timeutil の「tz」を利用して、次のようにタイムゾーン設定をします。
tz.gettz( 'タイムゾーンのキーワード' )
### 日付にタイムゾーンを設定:datetimeとtimeutilのtzを利用
tz_utc = tz.gettz('UTC')
print(datetime(2023, 11, 15, 15, 30, 15, tzinfo=tz_utc))
tz_jp = tz.gettz('Japan')
print(datetime(2023, 11, 15, 15, 30, 15, tzinfo=tz_jp))
tz_tyo = tz.gettz('Asia/Tokyo')
print(datetime(2023, 11, 15, 15, 30, 15, tzinfo=tz_tyo))【実行結果】
1行目はUTC:協定世界時、2行目・3行目はJST:日本標準時です。

⑦ タイムゾーンの変換
日本標準時JSTを米国東部標準時ESTへ変換します。
なお、例で使う日付2023年11月15日はサマータイム期間外です。
datetime型の変数tに対して「astimezone(変換後のタイムゾーン)」を適用して変換します。
### 日本標準時JSTを米国東部標準時ESTへ変換:datetimeとtimeutilのtzを利用
tz_jp = tz.gettz('Japan')
t = datetime(2023, 11, 15, 15, 30, 15, tzinfo=tz_jp)
print('JST ->', t)
tz_est = tz.gettz('US/Eastern')
print('EST ->', t.astimezone(tz_est))【実行結果】
時差は14時間です。
テキストの5時間差の出し方は未だ分かっていません。。。
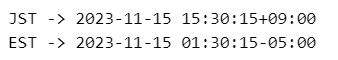
⑧ タイムゾーン付き日付を書式指定して文字列変換
「%Z」でタイムゾーンの文字列表示ができます。
### タイムゾーン付き日時の書式表示:datetimeとtimeutilのtzを利用
# 日本標準時
tz_jp = tz.gettz('Japan')
t = datetime(2023, 11, 15, 15, 30, 15, tzinfo=tz_jp)
print(t.strftime('%Y年%m月%d日%H時%M分%S秒 %Z'))
# 米国東部標準時
tz_est = tz.gettz('US/Eastern')
t_est = t.astimezone(tz_est)
print(t_est.strftime('%b %d %A %X %Y %Z'))【実行結果】
JST、ESTの文字を表示できました。

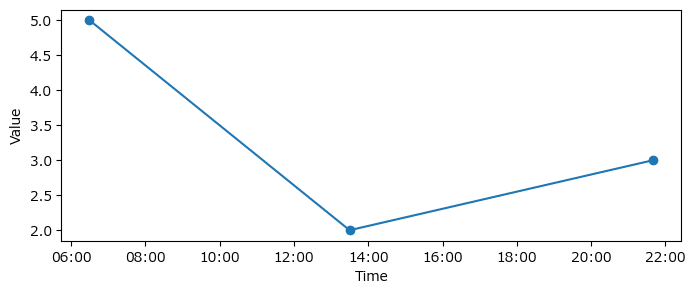
⑨ 時刻を用いた作図
datetimeライブラリのtimeクラスを用いて時刻を表現します。
time( 時, 分, 秒 )
作図にはpandasのplot関数を用いています。
テキストの図2.16に相当します。
### 時刻を用いた作図 ※図2.6に相当
## データの作成
# x:日時、y:値を設定
x = [time(6, 30, 0), time(13, 30, 0), time(21, 40, 0)]
y = [5, 2, 3]
# データフレーム化
time_df = pd.DataFrame({'y': y}, index=x)
## 描画
ax = time_df.plot(figsize=(8, 3), style='o-', xlabel='Time', ylabel='Value',
legend=False)
ax.set_xticks([f'{i}:00' for i in range(6, 23, 2)]);【実行結果】
時刻をx軸ラベルに表示できました。
最後のコードで、x軸目盛り(xticks)に6:00~22:00をセットしたリスト(リスト内包表記)を渡しています。
2.3.2 時系列データを取り扱うためのクラス
テキストはRの「tsクラス」の操作方法を取り扱っています。
しかしPythonには、tsクラスに合致するデータ型等が(たぶん)無いです。
そこでこの記事では、pandasのデータフレームを対象にして、日付インデックスを用いたテキストの作図再現を検討します。
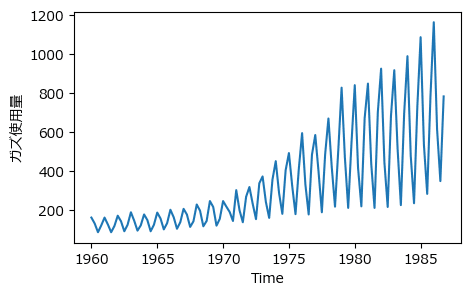
① UKgasデータの描画
statsmodelsのget_rdatasetを用いてRのデータセットからUKgasデータセットを取得した上で、グラフを描画します。
グラフ描画にはmatplotlibを利用しています。
テキストの図2.7左に相当します。
### 図2.7 UKgasデータの描画
## UKgasデータセットの読み込み
# 第1引数:Item, 第2引数:Package
data_ukgas = sm.datasets.get_rdataset('UKgas', 'datasets')
## 描画
plt.figure(figsize=(5, 3))
# 折れ線グラフの描画
plt.plot(data_ukgas.data.time, data_ukgas.data.value)
# 修飾
plt.xlabel('Time')
plt.ylabel('ガズ使用量')
plt.show()【実行結果】
時間経過とともに使用量が増えています。
また、季節変動の振幅が大きくなっているように見えます。
Rのggplot2を用いたテキスト図2.7の右側に類似する見栄えにするには、描画の前に次の呪文を唱えます(実行します)。
plt.style.use('ggplot')
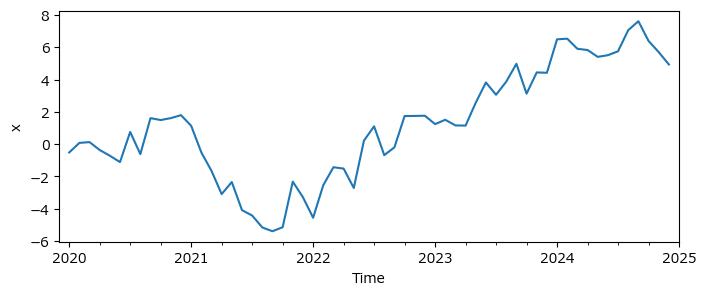
② ランダムウォークの描画
x軸に用いる年月のインデックスをpandasのperiod_rangeで作成します。
ランダムウォーク変数xと年月インデックスを用いてpandasのデータフレームを作成し、pandasのplotで描画します。
テキストの図2.8に相当します。
### 図2.8 ランダムウォークの描画
# 乱数シードの設定
np.random.seed(9999)
# 年月インデックスの作成 YYYY-MM
month_idx = pd.period_range(start='2020-01-01', freq='M', periods=60)
# ランダムウォークデータの作成
x = np.cumsum(np.random.randn(60))
# 年月インデックスとランダムウォークデータをデータフレーム化
df_randomwalk = pd.DataFrame({'x': x}, index=month_idx)
# データフレームの描画
df_randomwalk.plot(figsize=(8, 3), legend=False, xlabel='Time', ylabel='x',
xlim=('2019-12', '2025-01'))
plt.show()【実行結果】
x軸目盛りは「年」表示になりました。年月から年に変換できています。
なお、テキストの乱数生成と一致しないため、グラフも一致しません。
③ 時系列の切り出し
Rのtsクラスに装備された「window()」に相当するPythonの機能を見つけられなかったので、力技で指定期間を切り出して、pivot_tableで表にしました。
テキストの図2.9に相当します。
### 図2.9 時系列の切り出し
window = df_randomwalk.loc['2020-01':'2021-03', :]
window.pivot_table(index=window.index.year, columns=window.index.month,
values='x')【実行結果】

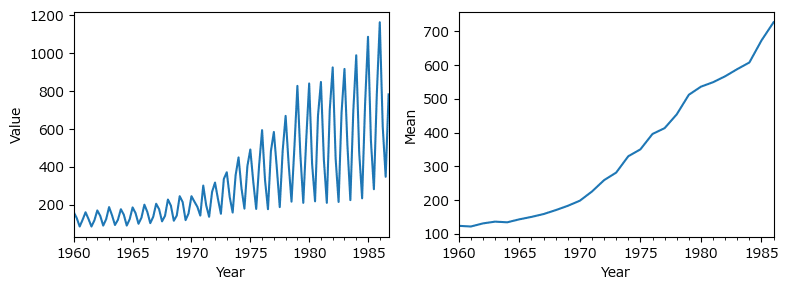
④ 整然データとして扱う
テキストでは、時系列データを整然データの形式にして扱うことを説明するために、Rのtidyverseパッケージを用いています。
一方、ここまでの処理で利用したPythonのpandasのデータフレーム形式のデータは、整然データといえば整然データなのかな?、ですので、改めて新しいことをする必要は無さそうです。
テキストの図2.10の作図を試してみます。
### 図2.10 イギリスのガスの使用量データの原系列(左)と年ごとの平均系列(右)
## データの準備
# UKgasデータをデータフレームに格納
ukgus_df = data_ukgas.data
# 四半期インデックスの作成
q_idx = pd.period_range(start='1960-01-01', freq='Q', periods=108)
# UKgasデータフレームのindexを四半期インデックスに置き換え
ukgus_df.set_index(q_idx, inplace=True)
# UKgasのvalueの年平均値を計算してukgus_df_yearに格納
ukgus_df_year = ukgus_df.resample(rule='A').mean().rename(columns=
{'value': 'mean'})
## 描画
fig, ax = plt.subplots(1, 2, figsize=(8, 3))
# 原系列のプロット
ukgus_df['value'].plot(ax=ax[0], xlabel='Year', ylabel='Value')
# 年平均系列のプロット
ukgus_df_year['mean'].plot(ax=ax[1], xlabel='Year', ylabel='Mean')
# 修飾
plt.tight_layout()
plt.show()【実行結果】
折れ線グラフの描画にはpandasのplotを利用しています。
2.4.1 時系列データの操作
時系列のデータに特有の操作である「ラグ」・「階差」を検討します。
① ラグ
基準時点からの時間のずれをラグと呼びます。
基準時点を$${t}$$とするとき、時点$${t-1}$$はラグ=1、時点$${t-2}$$はラグ=2です。
pandasのデータフレームの年月インデックスを12ヶ月=ラグ12、ずらしてみます。
単に年月インデックスを$${-12}$$しているだけです。
### ラグ
## 2020年1月から始まるデータの作成
# 年月インデックスの作成 YYYY-MM
month_idx = pd.period_range(start='2020-01-01', freq='M', periods=120)
# 変数xの作成
x = list(range(1, 121))
# データフレームの作成
df = pd.DataFrame({'x': x}, index=month_idx)
## 1年前にずらしたデータの作成
# 年月インデックスを12か月前にずらす:index-12
df.index = df.index - 12
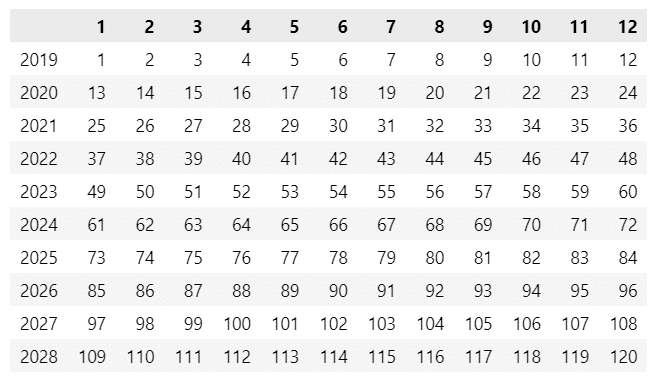
# 行:年、列:月のクロステーブル形式で表示
df.pivot_table(index=df.index.year, columns=df.index.month, values='x')【実行結果】
2019年始まりになりました。
② ラグ系列
元になる原系列データxから1期先、1期前にずらしたラグ系列データを作成します。
pandasのshiftでラグの値を引数に与えて実行します。
# ラグ系列でデータフレームを作成する :shiftでラグを算出
df = pd.DataFrame({'x': list(range(1, 11))}) # x(1~10)のデータフレーム作成
df['lead'] = df['x'].shift(-1) # 1期先leadを追加 -1
df['lag'] = df['x'].shift(1) # 1期前lagを追加 1
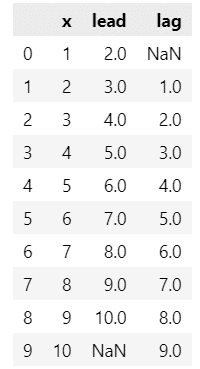
display(df)【実行結果】
leadは1期先、lagは1期前です。
それぞれ前後に1期ずらしたことにより、欠損値NaNが生じます。
③ 階差
階差は前後の値の差分です。
numpyのdiffで階差を計算します。引数nで階差の数を指定します。
### 図2.11 1階階差のイメージ numpyのdiffで算出 引数nで階差を指定
x = np.cumsum(range(0, 11))
print('x :', x)
print('1階階差:', np.diff(x, n=1))
print('2階階差:', np.diff(x, n=2))【実行結果】
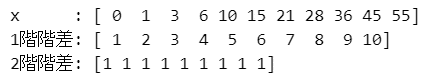
2.4.3 移動平均
移動平均は前後の一定期間の平均をとる系列データです。
例えば株価の移動平均線です。
$${m_{t,n} = \cfrac{1}{n} \sum_{k=0}^{n-1} y_{t-k}, \quad t=1, 2, \cdots}$$
pandasのrollingの引数で窓長を指定し、続けて、適用する関数を指定します。
移動「平均」を求めるので、適用する関数はmeanです。
df.rolling( 窓長 ).mean()
グラフ描画にはpandasのplotを利用しています。
テキストの図2.13に相当します。
なお、テキストの乱数生成と一致しないため、グラフも一致しません。
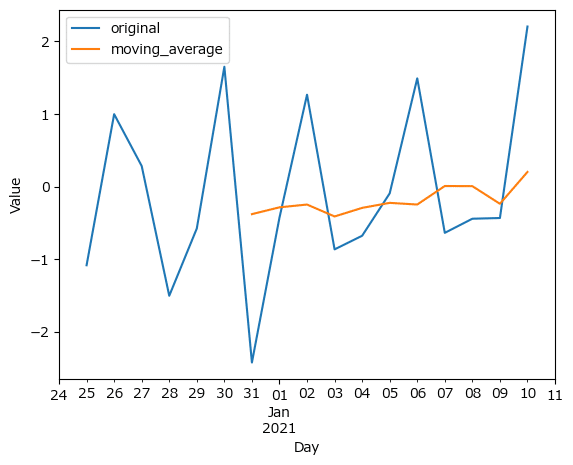
### 図2.13 原系列と移動平均
## 初期値設定
np.random.seed(123)
## データの作成
# 日付インデックスの作成 YYYY-MM-dd
day_idx = pd.date_range(start='2020-12-25', end='2021-01-10')
# 変数xの作成:標準正規分布の乱数
data_original = np.random.randn(len(day_idx))
# データフレーム化
moving_ave_df = pd.DataFrame({'original': data_original}, index=day_idx)
## 移動平均の算出
moving_ave_df['moving_average'] = moving_ave_df.rolling(7).mean()
## 描画
moving_ave_df.plot(xlabel='Day', ylabel='Value',
xlim=('2020-12-24', '2021-01-11'));【実行結果】
オレンジ色の移動平均線は7期目からスタートしています。
2.4.4 移動相関
移動相関は2つの時系列データの相関を「窓」をずらしながら求めます。
pandasのrollingで窓長20を指定して、corrで相関係数を求めます。
### 移動相関
# 初期値設定
np.random.seed(123)
# データの作成:pandasのデータフレーム
df = pd.DataFrame({'x1': np.random.randn(50), 'x2': np.random.randn(50)})
# 移動相関の算出:pandasのrolling.corrを利用
rolling_corr = df['x1'].rolling(window=20).corr(df['x2'])
rolling_corr[19:].values【実行結果】

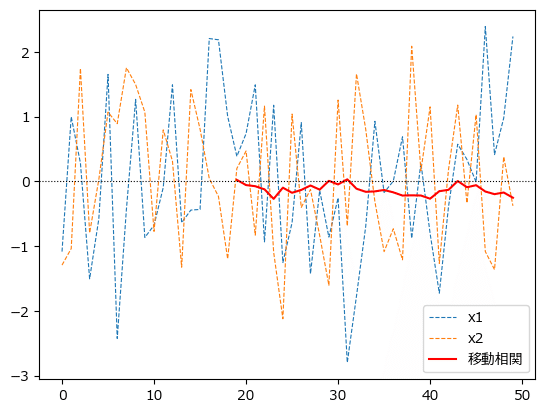
折れ線グラフにしてみましょう。
### 描画
plt.plot(df['x1'], lw=0.8, ls='--')
plt.plot(df['x2'], lw=0.8, ls='--')
plt.plot(rolling_corr, color='red')
plt.axhline(0, color='black', lw=0.8, ls=':')
plt.legend(['x1', 'x2', '移動相関']);【実行結果】
移動相関(相関係数)は0付近のようです。
第2章 後編へ続く
■次回の取り組みテーマ
自己相関、変動分解、ARモデル、ARIMAモデル、ARIMAXモデル
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
