
4-5 2段階実験確率変数の期待値 ~ 組み合わせとサイコロと袋の中の赤玉と
今回の統計トピック
「サイコロを振る事象」と「袋から玉を引く事象」を掛け合わせたときの期待値の計算について学びます!
類似問題を一緒に解きましょう。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
確率の分野
問5 2段階実験確率変数の期待値(サイコロを振って袋から玉を取り出す)
試験実施年月
統計検定2級 2019年6月 問8(回答番号15)
問題
公式問題集をご参照ください。
解き方
題意
サイコロを1回投げて出た目によって袋が決まり、袋から玉を2つ引く試行をします。
玉を引いたらすぐに袋に戻す「復元抽出」です。
1度の試行で赤い玉を引く回数を確率変数$${X}$$とするとき、$${X}$$の期待値$${E[X]}$$を求めます。
赤い玉を引く回数$${X}$$は$${ \{0, 1, 2 \} }$$の値を取ります。
赤い玉を引く回数が0回の確率$${\boldsymbol{P(X=0)}}$$
$$
\begin{align*}
&P(X=0)\\
&=サイコロが2以下の確率「2/6」\\
&\times 袋\mathrm{A}から2回連続で白い玉を引く確率「_2C_0 \times 3/5 \times 3/5」\\
&+サイコロが3以上の確率「4/6」\\
&\times 袋\mathrm{B}から2回連続で白い玉を引く確率「_2C_0 \times 4/5 \times 4/5」\\
&=18/150+64/150=82/150=41/75
\end{align*}
$$
赤い玉を引く回数が0回($${X=0}$$)の確率$${P(X=0)}$$は 41/75 です。
赤い玉を引く回数が1回の確率$${\boldsymbol{P(X=1)}}$$
$$
\begin{align*}
&P(X=1)\\
&=サイコロが2以下の確率「2/6」\\
&\times 袋\mathrm{A}から赤い玉を1つ、白い玉を1つ引く確率「_2C_1 \times 2/5 \times 3/5」\\
&+サイコロが3以上の確率「4/6」 \\
&\times 袋\mathrm{B}から赤い玉を1つ、白い玉を1つ引く確率「_2C_1 \times 1/5 \times 4/5」\\
&=24/150+32/150=28/75
\end{align*}
$$
赤い玉を引く回数が1回($${X=1}$$)の確率$${P(X=1)}$$は 28/75 です。
赤い玉を引く回数が2回の確率$${\boldsymbol{P(X=2)}}$$
$$
\begin{align*}
&P(X=2)\\
&=サイコロが2以下の確率「2/6」\\
&\times 袋\mathrm{A}から2回連続で赤い玉を引く確率「_2C_2 \times 2/5 \times 2/5」\\
&+サイコロが3以上の確率「4/6」 \\
&\times 袋\mathrm{B}から2回連続では赤い玉を引く確率「_2C_2 \times 1/5 \times 1/5」\\
&=8/150+4/150=6/75
\end{align*}
$$
赤い玉を引く回数が2回($${X=2}$$)の確率$${P(X=2)}$$は 6/75 です。
赤い玉を引く回数$${\boldsymbol{X}}$$の期待値
離散型の確率変数$${X}$$の期待値$${E[X]}$$は、$${E[X]\equiv \sum_i x_i f(x_i)}$$です。
赤い玉を引く回数$${X=0,1,2}$$ごとに確率$${P(X=0), P(X=1), P(X=2)}$$を掛けてから、3つの値を合計することによって、期待値を求めることができます。
$$
E[X]=0回\times41/75+1回\times28/75+2回\times6/75=40/75=8/15
$$
赤い玉を引く回数$${X}$$の期待値$${E[X]}$$は$${8/15}$$回です。
■ちなみに情報
期待値を求める際に、赤い玉を引く回数が0回の場合、$${0 \times 確率P(X=0)=0}$$となり、計算結果が0になります。
試験対策の観点では、赤い玉を引く回数が0回の場合の確率計算を端折って、スピードアップをはかることが可能です。
解答
⑤ 8/15 です。
難易度 ふつう
・知識:組み合わせの確率、期待値
・計算力:数式組み立て(中)、電卓(中)
・時間目安:2分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、類似問題を一緒に解いて、複雑な確率と期待値の計算を確認してまいりましょう!
お題
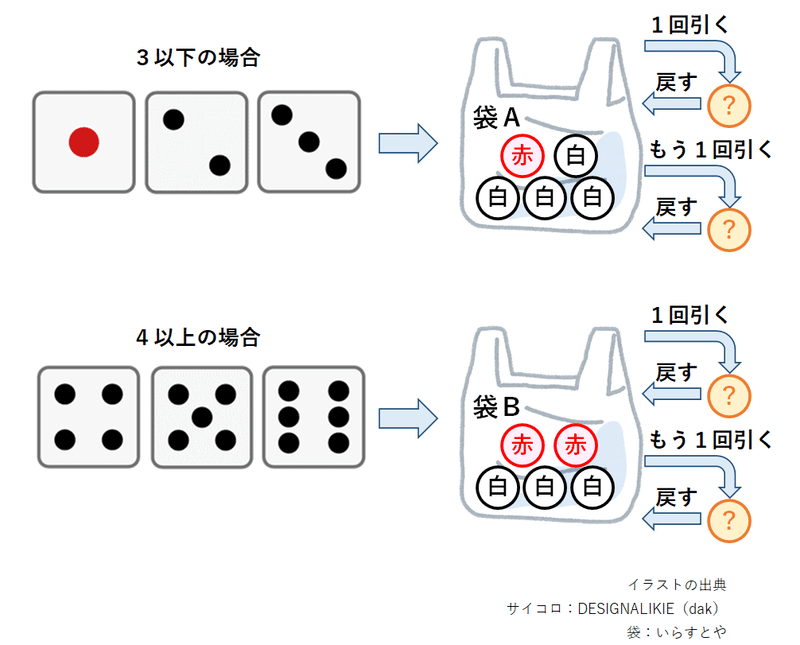
図のようにサイコロを1回投げて出た目によって袋が決まり、袋から玉を2つ引く試行をします。
玉を引いたらすぐに袋に戻す復元抽出です。
1度の試行で赤い玉を引く回数を確率変数$${X}$$とするとき、$${X}$$の期待値$${E[X]}$$を求めます。
確率と期待値
📕公式テキスト:2.1 事象と確率(55ページ~)、2.2 条件付き確率(59ページ~)、2.5 期待値と分散(67ページ~)
赤い玉を引く回数$${X}$$は$${ \{0, 1, 2 \} }$$の値を取ります。
サイコロの目が3以下になる事象(4以上になる余事象)、袋から1つ引いて赤い玉になる事象(白い玉になる余事象)、さらに袋からもう1つ引いて赤い玉になる事象(白い玉になる余事象)はそれぞれ、独立した事象ですので、積事象の確率($${P(A \cap B \cap C)}$$など)は各事象の確率の積($${P(A) \times P(B) \times P(C)}$$など)になります。
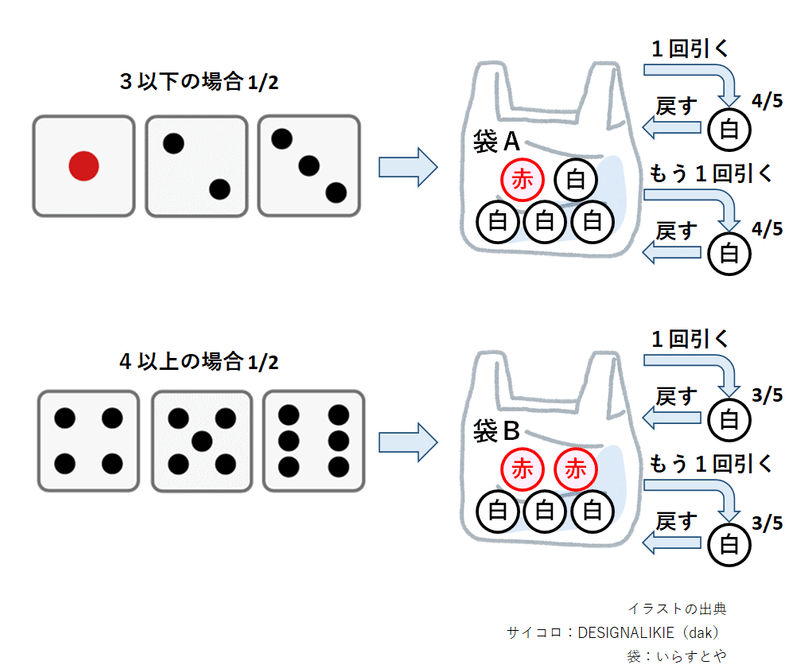
赤い玉を引く回数が0回の確率$${\boldsymbol{P(X=0)}}$$
■場合分け1:サイコロの目
まず、サイコロの目が3以下の確率は$${1/2}$$、4以上の確率は$${1/2}$$です。
■場合分け2-1:袋A
次にサイコロの目が3以下の場合、袋Aから玉を2回、復元抽出で引きます。
引く回数$${n}$$が2回で、そのうち赤い玉を引く回数$${x}$$が0回の場合は、組み合わせ$${_nC_x}$$の記号で表すと$${_2C_0}$$です。
組み合わせ$${C}$$の計算は次のとおりです。
$$
_nC_x=\cfrac{n \times n-1 \times \cdots \times n-x+1}{x \times x-1 \times \cdots \times 1}
$$
$$
ただし、_nC_n =\ _nC_0 = 1
$$
$${_2C_0}$$は1です。
袋Aには5個中、赤い玉が1つ含まれています。
2回引くときに赤い玉を引かない確率は白い玉を2回引く確率と同じであり、$${4/5 \times 4/5}$$です。
以上をまとめます。
$$
\begin{align*}
&サイコロが3以下の確率「1/2」\\
&\times 袋\mathrm{A}から2回連続で白い玉を引く確率「_2C_0 \times 4/5 \times 4/5」\\
\end{align*}
$$
■場合分け2-1:袋B
次にサイコロの目が4以下の場合、袋Bから玉を2回、復元抽出で引きます。
赤い玉を引く回数$${x}$$が0回の場合は、組み合わせ$${_2C_0=1}$$です。
袋Bには5個中、赤い玉が2つ含まれています。
2回引くときに赤い玉を引かない確率は白い玉を2回引く確率と同じであり、$${3/5 \times 3/5}$$です。
以上をまとめます。
$$
\begin{align*}
&サイコロが4以上の確率「1/2」\\
&\times 袋\mathrm{B}から2回連続で白い玉を引く確率「_2C_0 \times 3/5 \times 3/5」
\end{align*}
$$
■総合します
以上をさらにまとめて、確率を計算します。
$$
\begin{align*}
&P(X=0)\\
&=サイコロが3以下の確率「1/2」\\
&\times 袋\mathrm{A}から2回連続で白い玉を引く確率「_2C_0 \times 4/5 \times 4/5」\\
&+サイコロが4以上の確率「1/2」\\
&\times 袋\mathrm{B}から2回連続で白い玉を引く確率「_2C_0 \times 3/5 \times 3/5」\\
&=1/2 \times (1 \times 4/5 \times 4/5)+1/2 \times(1 \times 3/5 \times 3/5)\\
&=16/50+9/50\\
&=25/50
\end{align*}
$$
同じように、赤い玉を引く回数が1回のケースと2回のケースを考えます。
赤い玉を引く回数が1回の確率$${\boldsymbol{P(X=1)}}$$
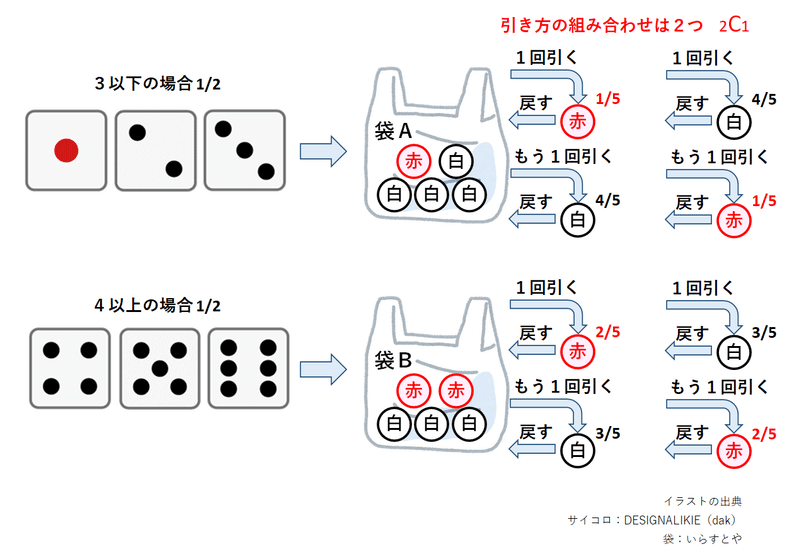
赤い玉を引く回数$${x}$$が1回の場合は、組み合わせ$${_2C_1=2/1=2}$$です。
サイコロの目が3以下の場合、袋Aから2回引くときに、赤い玉を1つ、白い玉を1つ引く確率は$${1/5 \times 4/5}$$です。
サイコロの目が4以上の場合、袋Bから2回引くときに、赤い玉を1つ、白い玉を1つ引く確率は$${2/5 \times 3/5}$$です。
以上をまとめて、確率を計算します。
$$
\begin{align*}
&P(X=1)\\
&=サイコロが3以下の確率「1/2」\\
&\times 袋\mathrm{A}から赤い玉を1つ、白い玉を1つ引く確率「_2C_1 \times 1/5 \times 4/5」\\
&+サイコロが4以上の確率「1/2」\\
&\times 袋\mathrm{B}から赤い玉を1つ、白い玉を1つ引く確率「_2C_1 \times 2/5 \times 3/5」\\
&=1/2 \times (2 \times 1/5 \times 4/5)+1/2 \times (2 \times 2/5 \times 3/5)\\
&=8/50+12/50\\
&=20/50
\end{align*}
$$
赤い玉を引く回数が2回の確率$${\boldsymbol{P(X=2)}}$$
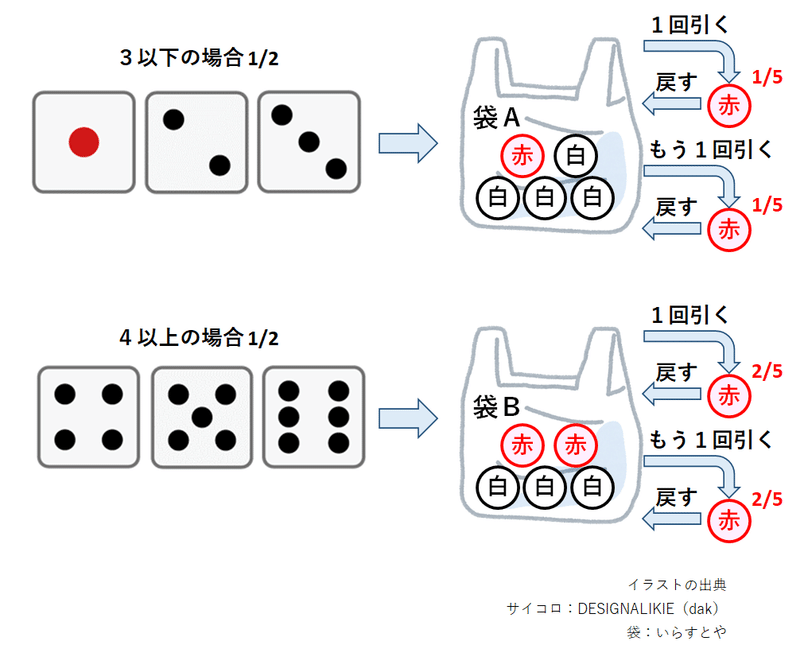
赤い玉を引く回数$${x}$$が2回の場合は、組み合わせ$${_2C_2=1}$$です。
サイコロの目が3以下の場合、袋Aから2回引くときに、赤い玉を2つ引く確率は$${1/5 \times 1/5}$$です。
サイコロの目が4以上の場合、袋Bから2回引くときに、赤い玉を2つ引く確率は$${2/5 \times 2/5}$$です。
以上をまとめて、確率を計算します。
$$
\begin{align*}
&P(X=2)\\
&=サイコロが3以下の確率「1/2」\\
&\times 袋\mathrm{A}から2回連続で赤い玉を引く確率「_2C_2 \times 1/5 \times 1/5」\\
&+サイコロが4以上の確率「1/2」\\
&\times 袋\mathrm{B}から2回連続で白い玉を引く確率「_2C_2 \times 2/5 \times 2/5」\\
&=1/2 \times (1 \times 1/5 \times 1/5)+1/2 \times (1 \times 2/5 \times 2/5)\\
&=1/50+4/50\\
&=5/50
\end{align*}
$$
赤い玉を引く回数$${\boldsymbol{X}}$$の期待値
離散型の確率変数$${X}$$の期待値$${E[X]}$$は、$${E[X]\equiv \sum_i x_i f(x_i)}$$(各回数とその確率を掛けた値を合計する)です。
$$
E[X]=0回\times25/50+1回\times20/50+2回\times5/50=30/50=3/5
$$
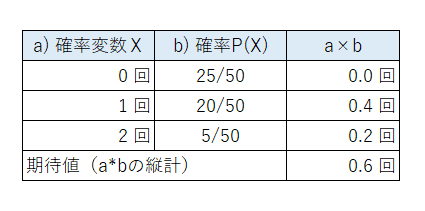
赤い玉を引く回数$${X}$$の期待値$${E[X]}$$は$${3/5=0.6}$$回です。
実践する
今回はお休みです。
「知る」のお題を解いてみましょう!
電卓・手作業で作成してみよう!
今回はお休みです。
EXCELで作成してみよう!
今回はお休みです。
EXCELサンプルファイルのダウンロード
今回はファイル提供はありません。
Pythonで作成してみよう!
今回はお休みです。
Pythonサンプルファイルのダウンロード
今回はファイル提供はありません。
おわりに
組み合わせ$${_nC_x}$$が出ました!
この組み合わせは二項分布の確率に登場します。
【二項分布】
成功確率$${p}$$のベルヌーイ試行を$${n}$$回行うときの成功回数を表す確率変数$${X}$$の確率分布は、二項分布$${Bin(n,p)}$$に従います。
確率変数$${X=x}$$の確率質量関数は次のようになります。
$$
P(X=x) \equiv f(x) =\ _nC_x \ p^x \ (1-p)^{n-x} \qquad (x=1, 2, \cdots, n)
$$
成功確率が$${p}$$、成功回数が$${x}$$、失敗確率が$${1-p}$$、失敗回数が$${n-x}$$です。
成功の組み合わせを考慮する必要があり、試行回数$${n}$$回のうちの成功回数$${x}$$の組み合わせ$${_nC_x}$$を乗じます。
【組み合わせの公式】
組み合わせ$${C}$$の計算は次のとおりです。
$$
\begin{align*}
_nC_x&=\cfrac{n!}{x!(n-x)!}\\
&=\cfrac{n \times n-1 \times \cdots \times n-x+1}{x \times x-1 \times \cdots \times 1}
\end{align*}
$$
二項分布の深掘りは別のテーマで。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
