
時系列分析入門【第4章 その3】ランダム切片モデル・潜在成長曲線モデル・多変量時系列の状態空間モデルをPythonとPyMC Ver.5 で実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第4章「RStanによる状態空間モデル」のRスクリプト・Stanコードをお借りして、PythonとPyMC Ver.5 で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは3つの状態空間モデルです。
1.パネルデータの分析(ラットの体重データ)
・ランダム切片モデル
・潜在成長曲線モデル
2.多変量時系列の解析(平面移動軌跡データ)
・Correlated Random Walk (CRW) モデル
今回はPyMCでモデリングします。
いくつかのモデルは残念な結果になりました(泣)
まぁまぁ、諸々はさておいて、時系列分析とベイズモデリングを楽しんでいきましょう!
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第4章 RStanによる状態空間モデル
この記事は「4.2 観測値が連続量の場合」の4.2.3~4.2.4を実践いたします。
インポート(+環境準備)
この記事で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# Rデータセット
import statsmodels.api as sm
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# グラフ描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】PyMC環境の構築
AnacondaでPyMC環境を構築する方法を次のリンクの「pymc環境の構築」の箇所に記載しています。
ご参考まで。

パネルデータの分析:ランダム切片モデル
記事「時系列分析入門【第3章 後編】線形モデル(OLS、GLS)、一般化線形モデル、線形混合モデルをPythonで実践する」では statsmodels を用いて実験したランダム切片モデル、潜在成長曲線モデルについて、今回は状態空間モデルで実験します!
こちらは第3章後編記事のリンクです。
今回もラットの体重データを利用します。
ランダム切片モデルの数式です。
$$
\begin{align*}
Y_{it} &= \beta_{0i} + R_{it}, \quad R_{it} \sim \text{Normal}\ (0,\ \sigma^2_{R}) \\
\beta_{0i} &= \gamma_{00} + U_{0i}, \quad U_{0i} \sim \text{Normal}\ (0,\ \sigma^2_{U})
\end{align*}
$$
添字$${i}$$はラットの個体番号、$${t}$$は時間です。
なお、このランダム切片モデルのベイズモデリングでは、時間$${t}$$を用いていません。
$${Y_{it}}$$は$${t}$$時点の個体$${i}$$のラットの体重であり、目的変数です。
$${U_{0i}}$$はランダム効果であり、直接測定されない変数です。
$${\gamma_{00}}$$は固定効果です。

① データの読み込み・前処理
Rのnlmeパッケージのデータセット「BodyWeight」を statsmodels(sm) を利用して読み込み、Rスクリプトと同様の前処理を実施します。
### データセットの準備
# BodyWeightデータセットの読み込み
df_rat = sm.datasets.get_rdataset('BodyWeight', 'nlme').data
# 前処理
df_rat = df_rat[(df_rat['Diet'].isin((1, 2))) & ~(df_rat['Time']==44)]
df_rat['Time'] = ((df_rat['Time'] - 1) / 7).astype('int')
# 前処理後のデータの表示
display(df_rat)【実行結果】
12体のラットの10期の体重データです。
Ratはラットの個体番号、Dietは餌の種類(1か2)、timeは体重の測定時点(週)、weightは体重(g)です。

② モデルの定義
時系列分析では無いので、シンプルなモデルになりました。
gamma、sigmaR、sigmaUの事前分布はテキストと同じ内容です。
betaはラット$${i}$$ごとに推論します。
### モデルの定義
# 初期値設定:0始まりに変更
rat_idx = list(df_rat['Rat'].values - 1)
with pm.Model() as model_rat1:
### データ関連定義
# coordの定義
model_rat1.add_coord('data', values=df_rat.index, mutable=True)
model_rat1.add_coord('rat', values=df_rat['Rat'].unique(), mutable=True)
# dataの定義
y = pm.ConstantData('y', value=df_rat['weight'].values, dims='data')
ratIdx = pm.ConstantData('ratIdx', value=rat_idx, dims='data')
### 事前分布
# 事前分布
gamma = pm.Normal('gamma', mu=0, sigma=100)
sigmaR = pm.HalfCauchy('sigmaR', beta=5)
sigmaU = pm.HalfCauchy('sigmaU', beta=5)
# muの計算
beta = pm.Normal('beta', mu=gamma, sigma=sigmaU, dims='rat')
### 尤度
likelihood = pm.Normal('likelihood', mu=beta[ratIdx], sigma=sigmaR,
observed=y, dims='data')【実行結果】出力なし
③ モデルの表示・可視化
モデルの数式を表示します。
# モデルの表示
model_rat1【実行結果】

モデルを図にして可視化しましょう。
# モデルの可視化
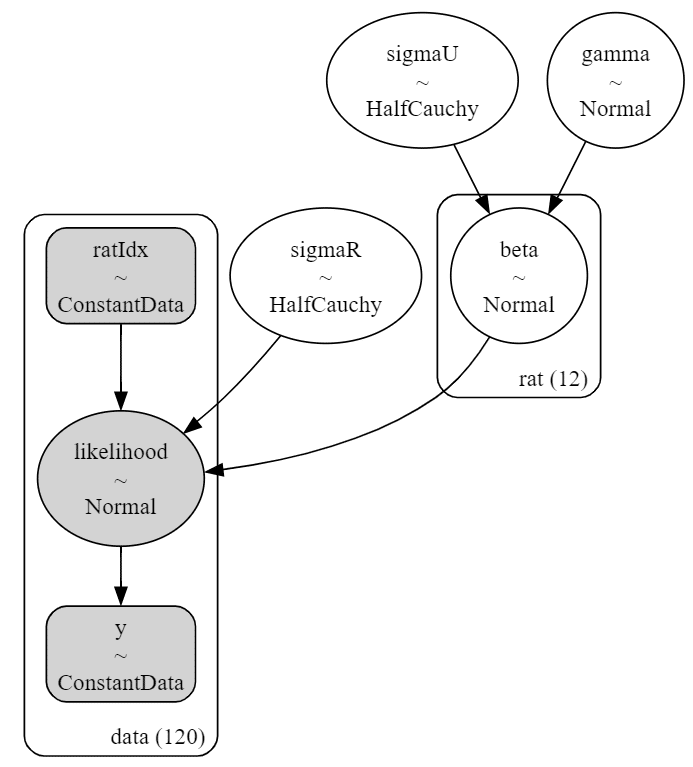
pm.model_to_graphviz(model_rat1)【実行結果】
目的変数$${y}$$(直接的にはlilelihood)と$${beta}$$が階層構造になっていることが分かります。
④ 事後分布からのサンプリング
MCMCを実行します。
NUTSサンプラーにnumpyroを利用します。
実行時間はおよそ25秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 25秒
with model_rat1:
idata_rat1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果(一部)】

⑤ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_rat1 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
var_names = ['gamma', 'sigmaR', 'sigmaU', 'beta']
pm.summary(idata_rat1, hdi_prob=0.95, var_names=var_names)【実行結果】
固定効果$${\gamma_{00}}$$は$${297.5}$$となりました。
各ラット$${i}$$の$${\beta_i}$$から$${\gamma_{00}}$$を差し引くと、ランダム効果$${U_{0i}}$$を求められると思います。
テキストおよびRコードに要約統計情報の正解が掲載されていないので、答え合わせはできませんでした。

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_rat1, combined=True, var_names=var_names, figsize=(10, 8))
plt.tight_layout();【実行結果】
収束している感じがします。

⑥ 事後予測サンプリングの実行
目的変数「y」の事後予測を行って描画します。
### 事後予測のサンプリングの実施
with model_rat1:
idata_rat1.extend(pm.sample_posterior_predictive(idata_rat1,
random_seed=1234))【実行結果】
ときどき、プログレスバーに実行を示す緑色が出ないときがあります。

「y」の事後予測サンプリングデータをplot_ppcを用いて描画します。
### 事後予測のプロット
fig, ax = plt.subplots(figsize=(10, 4))
pm.plot_ppc(idata_rat1, num_pp_samples=100, random_seed=1234, ax=ax)
ax.set(xlabel='Weight(kg)', ylabel='density', title='事後予測プロット');【実行結果】
黒い線が観測値のKDE、オレンジの点線が事後予測の平均値です。
300~550gの範囲は予測がハマっている感じがします。
この範囲を超えると少々、予測がブレています。


パネルデータの分析:潜在成長曲線モデル
引き続きラットの体重データを用いて分析を進めます。
潜在成長曲線モデルの数式です。
$$
\begin{align*}
Y_{it} &= \beta_{0i} + \beta_{1i} X_{it} + R_{it} \\
\beta_{0i} &= \gamma_{00} + U_{0i} \\
\beta_{1i} &= \gamma_{10} + U_{1i} \\
R_{it} &\sim \text{Normal}\ (0,\ \sigma^2_{R}) \\
\left(\begin{matrix} U_{0i} \\ U_{1i}\end{matrix}\right)
&=\text{Normal} \left[
\left( \begin{matrix} 0 \\ 0 \end{matrix} \right),
\left( \begin{matrix} \tau^2_{00} & \tau_{01} \\ \tau_{01} & \tau^2_{11}\end{matrix} \right)
\right]
\end{align*}
$$
添字$${i}$$はラットの個体番号、$${t}$$は時間です。
$${Y_{it}}$$は$${t}$$時点の個体$${i}$$のラットの体重であり、目的変数です。
$${X_{it}}$$は時間$${t}$$です。経過週数を示します。
$${\beta_{1i}}$$は経過日数の影響であり、変数$${X_{it}}$$に対する傾きの位置づけです。
そしてもっとも興味のあるパラメータです。
$${\beta_{0i}}$$はランダム切片モデルの$${\beta_{0i}}$$と同じです。
$${U_{0i},\ U_{1i}}$$は多変量正規分布に従います。
① モデルの定義
こちらのモデルも時系列特有の分布(ガウスランダムウォークや自己回帰モデル)を利用しません。
時間要素$${Time}$$を説明変数$${x}$$とし、$${\hat{y}}$$の線形式で用いています。
### モデルの定義
# 初期値設定:ラットの個体番号を0始まりにしてインデックスとします
rat_idx = list(df_rat['Rat'].values - 1)
with pm.Model() as model_rat2:
### データ関連定義
# coordの定義
model_rat2.add_coord('data', values=df_rat.index, mutable=True)
model_rat2.add_coord('rat', values=df_rat['Rat'].unique(), mutable=True)
model_rat2.add_coord('idx', values=[0, 1], mutable=True)
# dataの定義
y = pm.ConstantData('y', value=df_rat['weight'].values, dims='data')
x = pm.ConstantData('x', value=df_rat['Time'].values, dims='data')
ratIdx = pm.ConstantData('ratIdx', value=rat_idx, dims='data')
### 事前分布
# 事前分布
gamma = pm.Normal('gamma', mu=0, sigma=100, dims='idx')
sigmaR = pm.HalfCauchy('sigmaR', beta=5)
# cov=tau(chol)の計算
sd_dist = pm.Exponential.dist(1.0, shape=2)
tau, corr, stds = pm.LKJCholeskyCov('tau', n=2, eta=2, sd_dist=sd_dist,
compute_corr=True)
# muの計算
beta = pm.MvNormal('beta', mu=gamma, chol=tau, dims=('rat', 'idx'))
yHat = pm.Deterministic('yHat', beta[ratIdx, 0] + beta[ratIdx, 1] * x,
dims='data')
### 尤度
likelihood = pm.Normal('likelihood', mu=yHat, sigma=sigmaR,
observed=y, dims='data')【実行結果】出力なし
【補足】
$${beta}$$の多変量正規分布の共分散パラメータにはコレスキー分解された分散共分散行列$${tau}$$を指定しています。
$${tau}$$はpm.LKJCholeskyCov()で算出します。
このあたりの指定は正直なところよく分かっておりません。
そこで、PyMC公式サイトの pm.LKJCholeskyCov のコード例をそのまま利用させていただきました。
② モデルの可視化
変数名に「_」(アンダースコア)を含んでしまったのでモデルの数式を表示できません(自環境の問題かもしれません)。
モデルを図にして可視化しましょう。
# モデルの可視化
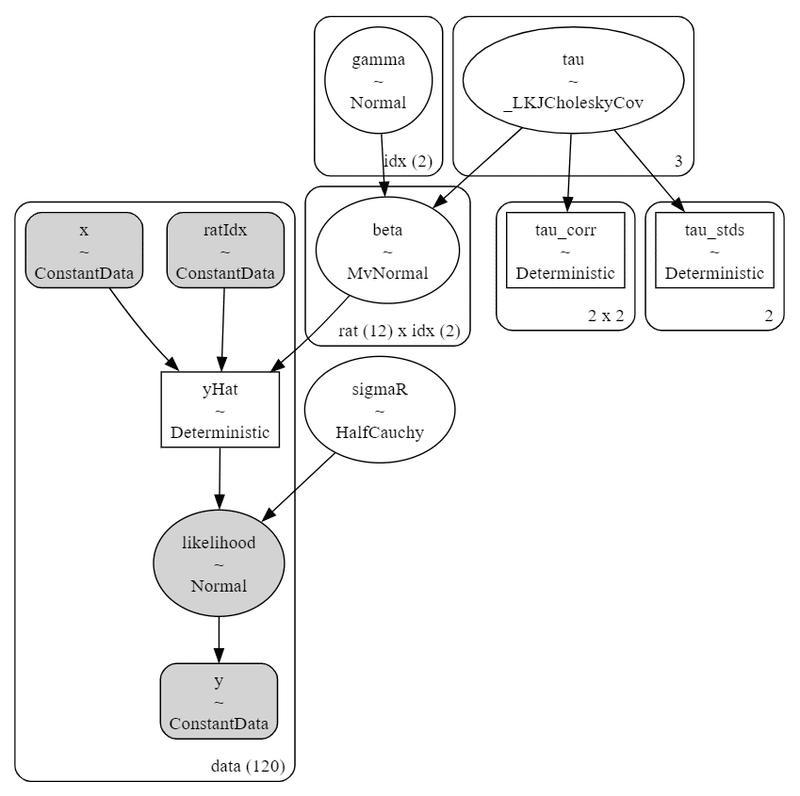
pm.model_to_graphviz(model_rat2)【実行結果】
$${beta}$$はラットの個体数$${12 \times 2}$$の行列です。
$${beta}$$の形状=3はおそらく、下三角行列に圧縮しているからだと思われます。
③ 事後分布からのサンプリング
MCMCを実行します。
NUTSサンプラーにnumpyroを利用します。
実行時間はおよそ15秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 15秒
with model_rat2:
idata_rat2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果(一部)】

④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_rat2 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
var_names = ['gamma', 'sigmaR', 'tau', 'beta']
pm.summary(idata_rat2, hdi_prob=0.95, var_names=var_names, filter_vars='like')【実行結果】
テキストのRコードに掲載された要約統計情報と一致しませんでした。

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_rat2, combined=True, var_names=var_names, figsize=(10, 8))
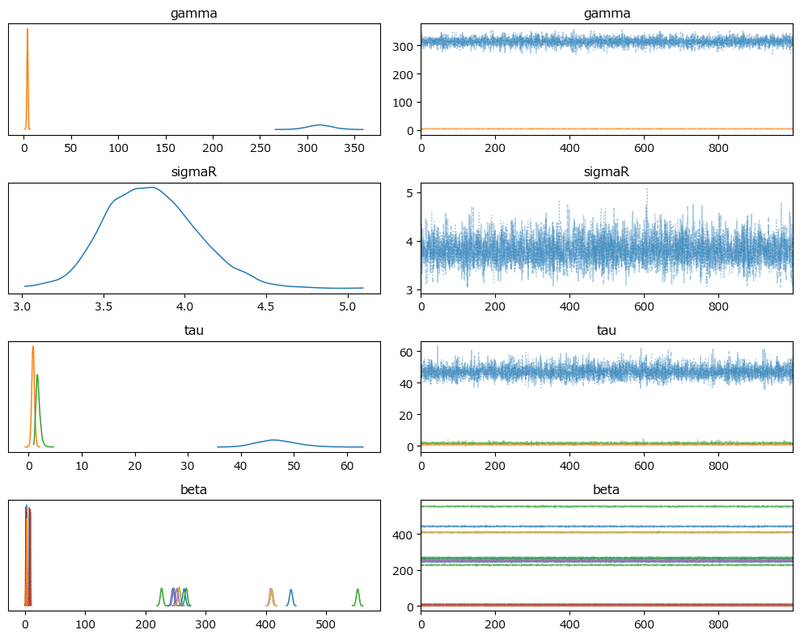
plt.tight_layout();【実行結果】
収束している感じがします。
⑤ 経過週数の影響を確認
$${\beta_{1i}}$$の値を個体別に確認します。
フォレストプロットを用いて描画します。
### 経過週数の影響β_1iの推定値
coords = {'idx': 1}
ax = pm.plot_forest(idata_rat2, hdi_prob=0.95, combined=True,
var_names=['beta'], coords=coords, figsize=(6, 4))
ax[0].set(title=r'経過週数の影響$\beta_{1i}$ の推定値', xlabel='g')
plt.tight_layout();【実行結果】
番号9,10,12のラットは他のラットと比べて、経過週数の影響が大きい様子が分かりました。

⑥ 事後予測サンプリングの実行
目的変数「y」の事後予測を行って描画します。
### 事後予測の乱数データの取得
with model_rat2:
idata_rat2.extend(pm.sample_posterior_predictive(idata_rat2,
random_seed=1234))【実行結果】

「y」の事後予測サンプリングデータをplot_ppcを用いて描画します。
### 事後予測のプロット
fig, ax = plt.subplots(figsize=(10, 4))
pm.plot_ppc(idata_rat2, num_pp_samples=100, random_seed=1234, ax=ax)
ax.set(xlabel='Weight(kg)', ylabel='density', title='事後予測プロット');【実行結果】
黒い線が観測値のKDE、オレンジの点線が事後予測の平均値です。
予測の線はかなり観測値にフィットしている感じがします。
ランダム切片モデルのグラフと比べてみて下さい。

(参考:ランダム切片モデルの事後予測プロット)

以上で、ラットの体重データを用いたパネルデータの分析は終わりです。

多変量時系列解析:CRWモデル
Correlation Random Walk モデル(CRWモデル)は移動軌跡(時間経過を伴う緯度・経度の移動)のモデリングに用いられるそうです。
強い観測ノイズが乗る移動軌跡データにも適用できる状態空間モデルであり、動物の位置ロガーデータの解析に用いられてきているようです。

CRWモデルの数式です。
急速に難易度が上がってまいりました(泣)
$$
\begin{align*}
\boldsymbol{Y}_t &= \boldsymbol{\alpha}_t + \boldsymbol{\varepsilon}_t \\
\boldsymbol{\alpha}_{t+1} &= \boldsymbol{\alpha}_t + \gamma \boldsymbol{Rv}_t + \boldsymbol{\eta}_t \\
\boldsymbol{\eta}_t &\sim \text{Normal}\ (\boldsymbol{0},\ \boldsymbol{\Sigma}_{\eta}) \\
\boldsymbol{\varepsilon}_t &\sim \text{Normal}\ (\boldsymbol{0},\ \boldsymbol{\Sigma}_{\varepsilon}) \\
\boldsymbol{\alpha}_t &= \left( \begin{matrix} x_{1,t} \\ x_{2,t}\end{matrix} \right) \\
\boldsymbol{R} &= \left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{matrix} \right) \\
\boldsymbol{v}_t &= \left( \begin{matrix} x_{1,t} - x_{1, t-1} \\ x_{2,t} - x_{2, t-1}\end{matrix} \right) \\
\end{align*}
$$
時間$${t}$$における位置$${\boldsymbol{\alpha}_t}$$は緯度・経度を示す2次元ベクトルであり、レベルに相当します。
$${\boldsymbol{v}_t}$$は速度であり、トレンドに相当します。
$${\boldsymbol{R}}$$は回転行列であり、個体がどちらかに曲がりがちという特徴を表します。
【おことわり】
データの期間をテキストの50期よりも大幅に減らして、16期としています。
自環境の問題かもしれませんが、17期以上に設定してMCMCを実行するとエラーが発生してしまいます。
エラーを回避するために泣く泣く減らしました(泣)

① データの作成
軌跡データを作成します。16期分です(N=16)。
上述のCRWモデルの数式に沿っていますので、モデル理解にも役立つと思います。
### 軌跡のシミュレーションデータの作成
# 初期値設定
np.random.seed(110)
N = 16 # 時点数 ※テキストは50
gamma = 0.95 # 速度にかかる係数
sigma_V = 0.01 # 観測ノイズ
sigma_W = 0.005 # システムノイズ
degree = 0.01 # 曲がる角度
x, y, muX, muY = np.zeros(N), np.zeros(N), np.zeros(N), np.zeros(N)
# CRWモデルに基づく軌跡
muX[1] = np.random.normal(loc=muX[0], scale=sigma_W, size=1)
muY[1] = np.random.normal(loc=muY[0], scale=sigma_W, size=1)
for t in range(2, N):
muX[t] = np.random.normal(
loc=muX[t-1] + gamma * ((np.cos(degree)*(muX[t-1]-muX[t-2])) \
- (np.sin(degree)*(muY[t-1]-muY[t-2]))),
scale=sigma_W, size=1)
muY[t] = np.random.normal(
loc=muY[t-1] + gamma * ((np.sin(degree)*(muX[t-1]-muX[t-2])) \
+ (np.cos(degree)*(muY[t-1]-muY[t-2]))),
scale=sigma_W, size=1)
# 観測値の作成
for t in range(N):
x[t] = np.random.normal(loc=muX[t], scale=sigma_V, size=1)
y[t] = np.random.normal(loc=muY[t], scale=sigma_V, size=1)
# データフレーム化
crw = pd.DataFrame({'x': x, 'y': y, 'muX': muX, 'muY': muY})
display(crw)【実行結果】
$${x,y}$$が観測された座標、$${muX, muY}$$が真の座標です。

描画しましょう。
テキストの図4.12の左・中に相当します。
### 描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 5), sharex=True, sharey=True)
ax1.plot(crw['muX'], crw['muY'])
ax1.set(title='真の座標', xlabel='muX', ylabel='muY')
ax2.plot(crw['x'], crw['y'])
ax2.set(title='観測された座標', xlabel='x', ylabel='y');【実行結果】
横軸 x と縦軸 y の平面上を、動物が移動した軌跡のように見えます。
観測された座標の方はノイズが加わってランダムなジグザク感が増しています。


② モデルの定義
尤度 likelihood は x と y に対応する2つの式で構成されます。
難関は「muX, muY の計算」です。
テキストのStanコードを真似ては見たものの、モデルの構造や推論結果はいかに…。
### モデルの定義
with pm.Model() as model_crw:
### データ関連定義
# coordの定義
model_crw.add_coord('data', values=crw.index, mutable=True)
# dataの定義
x = pm.ConstantData('x', value=crw['x'].values, dims='data')
y = pm.ConstantData('y', value=crw['y'].values, dims='data')
### 事前分布
# 事前分布
sigmaW = pm.HalfCauchy('sigmaW', beta=5)
sigmaV = pm.HalfCauchy('sigmaV', beta=5)
theta = pm.Beta('theta', alpha=1, beta=1)
gamma = pm.Beta('gamma', alpha=1, beta=1)
# 計算
degree = pm.Deterministic('degree', (2*theta-1)*np.pi)
### muX, muYの計算
muX = [0] * N
muY = [0] * N
muX[0] = pm.Normal('muX0', mu=0, sigma=100)
muY[0] = pm.Normal('muY0', mu=0, sigma=100)
muX[1] = pm.Normal('muX1', mu=muX[0], sigma=sigmaW)
muY[1] = pm.Normal('muY1', mu=muY[0], sigma=sigmaW)
for t in range(2, N):
muX[t] = pm.Normal(
'muX' + str(t),
mu=muX[t-1] + gamma*((pt.cos(degree)*(muX[t-1] - muX[t-2])) \
- (pt.sin(degree)*(muY[t-1] - muY[t-2]))),
sigma=sigmaW)
muY[t] = pm.Normal(
'muY' + str(t),
mu=muY[t-1] + gamma*((pt.sin(degree)*(muX[t-1] - muX[t-2])) \
+ (pt.cos(degree)*(muY[t-1] - muY[t-2]))),
sigma=sigmaW)
### 尤度
likelihoodX = pm.Normal('likelihoodX', mu=muX, sigma=sigmaV, observed=x,
dims='data')
likelihoodY = pm.Normal('likelihoodY', mu=muY, sigma=sigmaV, observed=y,
dims='data')【実行結果】出力なし
③ モデルの表示・可視化
モデルの数式を表示します。
# モデルの表示
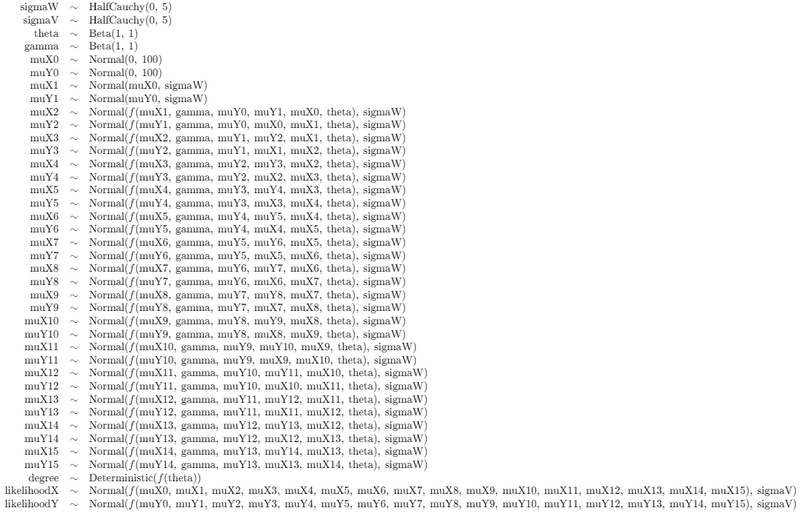
model_crw【実行結果】
数式が多いです!
変数 muX と muY は時系列 0~15 の計16個できあがっています。
モデルを図にして可視化しましょう。
# モデルの可視化
pm.model_to_graphviz(model_crw)【実行結果】
はいー!複雑ですー!
pymc_experimental.statespaceの状態空間モデルを使えないものかと思案はしてみたものの、muX と muY を相互クロスさせるようなモデル定義の方法を編み出せなかったので断念しました。

④ 事後分布からのサンプリング
MCMCを実行します。
NUTSサンプラーにnumpyroを利用します。
実行時間はおよそ45秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 45秒
with model_crw:
idata_crw = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果(一部)】


⑤ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_crw # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum().data_vars【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
(表示上、省略されたパラメータも0件になりました。)
パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
var_names = ['mu', 'sigma', 'theta', 'gamma', 'degree']
pm.summary(idata_crw, hdi_prob=0.95, var_names=var_names, filter_vars='like')【実行結果】
ぱっと見、極端な異常データは無さそうです。
ただし、データ作成時に用いた gamma, sigmaV, simgaW, thetaの値とは大きく乖離しています。
うまく推論できなかったようです(汗)

(参考:データ作成時に用いたパラメータの値)


トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_crw, combined=True, var_names=var_names, filter_vars='like',
figsize=(10, 20))
plt.tight_layout();【実行結果】
一部のパラメータのみの表示ですが、収束している感じがします。

⑥ 事後予測サンプリングの実行
目的変数「x」「y」の事後予測を行って描画します。
### 事後予測の乱数データの取得
with model_crw:
idata_crw.extend(pm.sample_posterior_predictive(idata_crw,
random_seed=1234))【実行結果】

「x」「y」の事後予測サンプリングデータをplot_ppcを用いて描画します。
### 事後予測のプロット
pm.plot_ppc(idata_crw, num_pp_samples=500, random_seed=1234, figsize=(10, 4));【実行結果】
黒い線が観測値のKDE、オレンジの点線が事後予測の平均値です。
右の「y」は事後予測が観測値にハマっているように見えます。
左の「x」は観測値の変動(?)がやや激しい感じであり、事後予測が観測値に追いつけていないように見えます。

⑦ 推測した軌跡の描画
テキストの図4.12に相当する軌跡の描画を行います。
最初に推論データから座標の平均値を算出します。
### 座標の推論データの平均値を取得
ax_x, ax_y = [], []
for i, val in enumerate((idata_crw.posterior.to_dataframe()
.reset_index().mean()[2:-5])):
if i % 2 == 0:
ax_x.append(val)
else:
ax_y.append(val)続いて描画。
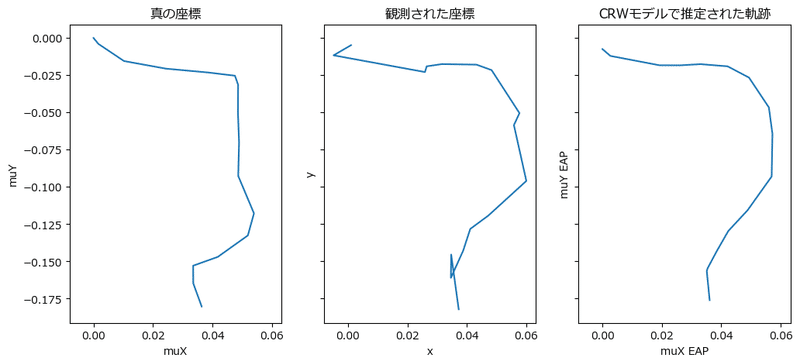
### 軌跡の描画 ※図4.12に相当
fig, ax = plt.subplots(1, 3, figsize=(12, 5), sharex=True, sharey=True)
ax[0].plot(crw['muX'], crw['muY'])
ax[0].set(title='真の座標', xlabel='muX', ylabel='muY')
ax[1].plot(crw['x'], crw['y'])
ax[1].set(title='観測された座標', xlabel='x', ylabel='y');
ax[2].plot(ax_x, ax_y)
ax[2].set(title='CRWモデルで推定された軌跡', xlabel='muX EAP', ylabel='muY EAP');【実行結果】
真の座標を捕捉できたとは言い難い結果となりました(汗)
残念です。

以上で終了です。
お疲れ様でした。
まとめ
パネルデータの分析では、ランダム切片モデルと潜在成長曲線モデルを学びました。
モデリングはできたものの、推論結果の適否はいまひとつした。
多変量時系列の解析では、CRWモデルで動物の移動軌跡の推論にチャレンジしました。
いろいろあって、残念な結果になりました。
(参考)推論データ(idata)の保存コード
pickle形式で保存します。
### idataの保存 pickle
import pickle
file = r'ch04_03_idata_rat1.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_rat1, f)
file = r'ch04_03_idata_rat2.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_rat2, f)
file = r'ch04_03_idata_crw.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_crw, f)読み込みコードは次のとおりです。
「file」のパス&ファイル名と「idata_rat1_load」を適宜変更してお使い下さい。
### idataの読み込み(例)
file = r'ch04_03_idata_rat1.pkl'
with open(file, 'rb') as f:
idata_rat1_load = pickle.load(f)第4章 その4 へ続く
■次回の取り組みテーマ
引き続き、状態空間モデルを学びます。
観測値が離散値のケースです。
・観測値が二項分布に従うモデル
・観測値がポアソン分布に従うモデル
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
