
『ホルスの目』から古代エジプトの2分法を学ぶ…1より小さい数の計算方法は?
どんな古代の言語にも、1より小さい数を表す「半分( half )」とか「四半分( quarter )」という単語があります。古代エジプトでは、これに加えさらに 八分、十六分、三十二分、六十四分までありました。今ではあまり使われませんが、日本語にも「八分」や「十六分」という表現があり、「八分の一」「十六分の一」という意味で使われます。日本語では「八分」のように「数詞+分」の形で表ますが、古代エジプトではこれらは単一の概念で、それぞれが一つの記号で表されていました。
図1は「ホルスの目」と呼ばれ、エジプトの壁画などによく描かれている呪力を持ったおまじないの絵です。ホルスはエジプトの最高神の一人で、敵役の神によって目をバラバラにされてしまいます。

図2のように、ホルスの目の部分は1/2, 1/4, 1/8, 1/16, 1/32, 1/64 を表しています。

『古代エジプトの数学』シリーズの記事では、古代エジプトの人々が自然数をどのように扱っていたのかを勉強してきました。数の発達はまず「自然数のかけ算、割り算」から始まります。古代エジプトでは自然数のかけ算や割り算は「2倍法」を使って計算していました。やがて古代エジプト人は1より小さい数としてホルスの目、つまり2進分数を考え出しました。2進分数のかけ算や割り算はどのように計算するのでしょうか。
私たちにはホルスの目のような特別な記号はありませんから、1より小さい数を次のように表します。

古代エジプトでは1/64まででしたが、任意の 1 / 2ⁿも許すことにします。また区切り記号としてセミコロン( ; )を使って表すことにします。セミコロンで区切られた部分は「 + 」と考えてください。次のように整数部を持つものも許されます。

このような表記を2進分数と呼びます。2進小数の場合は整数部も2進数で表す必要がありますが、2進分数の場合は整数部は10進数で表します。ここで『2進小数』や『2進分数』という表現を使いますが、これらの概念は近代になって確立されたものです。
2進分数は半分に割っても、2倍しても2進分数となります。たとえば 13 は次のように次々と半分に割ることができます。

2進分数は一番大きい分母に通分するとa / 2ⁿの形になります。たとえば、

となります。したがって、自然数のかけ算と割り算ができれば、2進分数のかけ算と割り算ができます。自然数のかけ算は2倍法では1行目を2倍していきましたが、1/2 していくことによっても計算できます。この方法を2分法と呼びます。次の図3 の表a では 1/2; 1/4; 1/32 × 32 の計算をしています。(32 は 2ⁿの形をしていますが、この形でなくてもかまいません。)表b は、25 ÷ 32 の計算です。この方法で m ÷ 2ⁿ の計算ができます。図3 の 表a と 表b は赤い文字の部分を除いて全く同じとなっていることに注意してください。実は、表 b は 25÷32 の計算で、表 aはその結果 1/2; 1/4; 1/32 の検算なのです。

かけ算の計算は以下(図4)のように行います。

(1) 右の欄の1行目にかける数「32 」を書き、2で割っていきます。
1になったら終わりです。
(2) 左の欄の1行目に「1」を書き、2で割っていきます。
(3) 「1/2, 1/4, 1/32」 が現われたらチェック欄にチェックを入れます。
(4) チェックがついたAns欄の数を合計したものが答え「25」 です。
割り算「m ÷ 2ⁿ」の計算は以下(図5)のように行います。

(1)右の欄の1行目に割る数「 32」を書き、2で割っていきます。1になったら終わりです。
(2)中央の欄(赤字で示した部分。以下、作業欄と呼びます)の1行目に割られる数「25 」を書きます
(3)作業欄から右の欄が引けるかをチェックします。引けたらチェック欄にㇾを記入し、作業欄の下の行に引いた結果を記入します。引けない場合は同じ数を記入します。これを一番下の行まで続けます。
(4) チェックがついたAns欄の数を合計したものが答え、すなわち 25 ÷ 32 の商となります。チェックを入れた行の右の欄を足すと目標の25 となっています。

かけ算(図4)と割り算(図5)は右の欄は32を順に2で割っていき、左の欄は1を2で割っていくという同じ計算をしています。違うのは、割り算 では目標が 25 であったのに対し、かけ算では目標が 1/2, 1/4, 1/32 となっていることです。
m / 2ⁿ の形の分数は図5の方法で2進分数に変換できます。
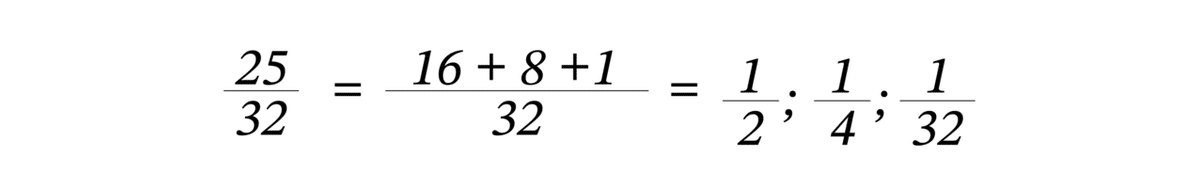
ここで、現代の数学でよく登場する式の変形方法をご紹介しましょう。数式の変換が多くなり少し難しく感じるかもしれませんが、この方法はよく使われる手法で今後も度々登場しますので、ここで簡単に説明しておきます。式の変換には次の規則を使います。

この規則を使って、図5で計算した 25/32 を2進分数に変換してみましょう。
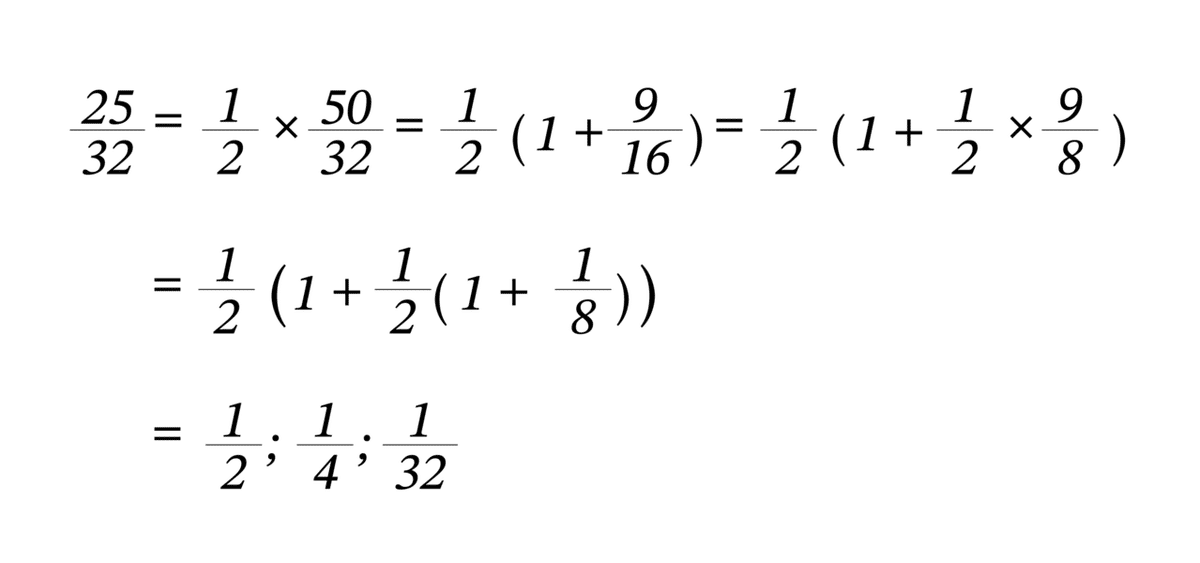
m / 2ⁿ の形にならない分数は無限2進小数となります。もちろん古代には無限小数などはありませんが、ここでは先ほどと同じ方法で、1/3を無限2進小数に変換してみます。

1/3 が現われたので以下この繰り返しとなります。

古代エジプトのパピルスに問題として書かれている割り算は、全て割り切れるもののようですが、2分法は割り切れない問題も計算することができます。ただし、適当なところで計算を打ち切らなければなりません。たとえば 2÷3 をやってみましょう。

右の欄は3を2で割っていき、作業欄から引けたら引きます。この操作はいくらでも続けることができますが、ここでは作業欄が 1/8 となったところで計算をやめました。右の欄のチェックされた欄と作業欄の一番下の 1/8 との和が2 ですから、2を3で割ると、答えは1/2;1/8 と未処理の1/8ということになります。
エジプト人は1より小さい数としてホルスの目、つまり2進分数を考え出しました。2進分数の場合、かけ算や割り算はどうのように計算したらよいのか? エジプト人は、2倍する代わりに半分にする方法、2分法を考え出しました。しかし、1/3 とか 1/5 などは2進分数では正確には表現できません。そこで、エジプト分数と呼ばれる分数に拡張しました。エジプト分数とはどのようなものなのでしょうか?次回の記事で調べてみたいと思います。
![]()
▼ 関連記事
▼数学Webマガジン・マテマティカ 『ピラミッドの謎』
エジプトのピラミッドには多くの謎が隠されています。マテマティカのWeb連載『ピラミッドの謎』では、ピラミッドの数に関する3つの謎「円周率の謎」「黄金比の謎」「地球の緯度の謎」を取り上げます。古代エジプトの歴史やエジプト神話など、様々な角度からピラミッドの謎に迫ります!
noteの『古代エジプトの数学』シリーズで扱っている「古代エジプトの数学能力」を知ることが謎を解く鍵になります。ぜひ合わせてご覧ください。
![]()
▼数学Webマガジン・マテマティカ 『数の発明』
私たち人類はいつ頃から「数」を扱うようになったのでしょうか。旧石器時代までの進化の時代、そして人類が農業というすばらしい手段を発明し、文明が興るまでの間にはどのような道のりがあったのでしょうか。人類が「数の概念」を獲得するまでの様子を見てみましょう。
▼数学Webマガジン・マテマティカ 『バビロニアの数』
皆さんは、むかし南メソポタミア地方に栄えたバビロニアという国をご存知でしょうか。最近になって太古の昔この地に高度な数学や天文学が発展していることが分かってきました。マテマティカWeb連載『 バビロニアの数 』では、60進数という記数法はどのようにして生まれたのか、バビロニアで行われていた高度な計算とはどのようなものだったのか、などバビロニア数学に焦点を当て詳しく紹介しています。ぜひご訪問ください!
▼Twitter、Webマガジンサイトも更新中。よろしくお願いいたします。
Twitter: @mathematicasite
Web:http://mathematica.site/
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?


