エジプト分数の割り算 Part1　〜拡張規則を使った計算〜

これまでのお話：エジプト分数のかけ算

　エジプト数学の特徴の一つは、エジプト分数と呼ばれる数を扱うことです。数回に渡ってエジプト分数のかけ算についてお話してきました。今回はエジプト分数の割り算です。私たちは小学校で分数のかけ算や割り算を勉強しますが、「分数の割り算の意味がよくわからない」というお子さんも多いようです。「どうして分数の割り算は分子と分母をひっくり返してかけるの？」と聞かれて答えに困った経験があるという方もいるかもしれません。分数を使っていた古代エジプトの人々は、分数の割り算をどのように計算していたのでしょうか？

　古代エジプトでは、2倍法や2分法を使ってエジプト分数のかけ算を行っていました。エジプト分数に現れる単位分数がすべて2進分数の場合は、この方法で比較的簡単に計算できますが、そうでない場合は計算が複雑になることがあります。古代エジプトの人々は表計算を簡単に処理するために2倍法を拡張しました。
【参考】：〔エジプト分数のかけ算：2倍法、2分法からの拡張〕

『 自然数÷自然数 』の復習

　エジプト分数の割り算の計算は、基本的には自然数の割り算と同じです。【参考】：〔古代エジプトの割り算〕

分数の割り算の前に、「自然数÷自然数」を復習しましょう。
　〔エジプト分数のかけ算：2倍法、2分法からの拡張〕で述べた拡張規則を使いますので説明をしておきます。「1120 ÷ 80」は以下のような表計算で行います。

　参考のため、14×80 の計算表も載せておきました。右側が割り算ですが、左のかけ算とまったく同じになっています。まず1行目に標題を書きます。割り算の場合、標題の1120 が「目標」で、合計が 1120 となるように右の欄の数を作っていきます。計算の手順を以下に示します。

　2行目は1行目を10倍し、800が得られます。目標から 800 を引いた 320 が次の目標です。3行目は1行目を2倍したもの、4行目は3行目を2倍したものです。ここで次の目標の 320 が得られます。チェックがついた左の欄の合計（この表の場合は14）が「1120÷80」の答えになります。この例の場合は「10倍」を使わなくても、2倍、4倍、8倍で実現できますが、10万とか100万といった大きな桁数になると、順次2倍していくより10倍した方が処理が早くなり、計算しやすかったのだと思います。

　このように、古代の人々は様々な計算に対応するために、2倍するだけでなく、任意の q に対して「q倍する」ことを許しました。ここで、このように拡張しても正しく計算していることを証明しましょう。

　表計算で c×a を計算する場合はまず、次の左のように標題と1行目を書き、b÷a を計算する場合は、次の右のように書きます。

　この1行目から開始し、すでにある行の左の欄と右の欄を同数倍し、新しい行を作ります。するとすべての行に対し、つねに次が成り立ちます。

　実際1行目では、左の欄＝1, 右の欄＝a だから成立します。ある行で (1) が成り立っているなら、左の欄と右の欄を同数倍しても (1) が成立します。
14×80 と 1120÷80 の計算表では、つねに

が成立しています。チェックがついた欄を足すと、かけ算の場合も割り算の場合も共に

を計算しています。したがって、

が成立します。

エジプト分数の割り算

　〔エジプト分数の考え方〕で「3個のパンを4人で分ける」問題を考えました。ここでは「 3÷4 」 を表計算で行ってみましょう。以下の表は2つとも「 3÷4 」の計算をしています。

　左の表は2分法で計算しています。1行目から1/2倍、1/2倍とし、「目標」の3になるように右の欄の数を作っています。チェックのついた左の欄（ Ans欄 ）の和が3÷4の答えです。ここでは 答えは「1/2 ; 1/4 」になります。 

　右の表はどのように計算しているのでしょうか。こちらも「目標」の3 になるように右の欄の数を作りますが、2分法とは違った手法を使っています。2行目は 4 に 2/3 をかけています。これは〔 2/3倍表：2/3の値を求めるために作られた表 〕を使って次のように計算します。

3行目から4行目の計算では 1 ; 1/3 を2で割り、2/3 となっています。これは〔 2倍表 ：2/mを単位分数に分解するための表 〕の 2/3の欄を逆方向に用います。

チェックのついた左の欄（ Ans欄 ）の和は2/3 ; 1/12 となっています。これが右の計算表で得られる答えです。古代エジプトの人々はこのような等式を自由に使いこなしていました。
　ここで見てきたように、「3個のパンを4人で分ける」という一つの問題に対し、計算方法によって2つの答え「1/2 ; 1/4」と「2/3 ; 1/12」が出てきました。2進分数をエジプト分数に発展させたことで、2進分数の持つ「表現の一意性」という性質は失ってしまいました。

割り算を計算するには…答えの予測が必要！

　〔エジプト分数の考え方〕では、任意の自然数 a と b に対し、b/a がエジプト分数で表わせることを示しました。a, b, c をエジプト分数とし、b/a ＝ c とします。すると c×a ＝ b となります。上で述べたように、b÷a の計算表は c×a の計算表と同じです。しかしこれは、「答えcが分かったら b÷a の計算表が作れる」ということを意味するだけで、実際に割り算を実現するには答え c を予測しなければなりません。これはなかなか大変で、多くの練習と経験が必要です。実際どんなものか見てみましょう。現代の皆さんはエジプト算法に熟達する必要はありませんから眺めるだけで結構です。説明を読みながら計算表を追いかけてみてください。

　古代エジプトでは次のように考えました。4個のパンをそれぞれ半分にすると1/2 のパンが8切れできます。このうち7切れを7人に分け、残りの1切れを7等分します。1/2の7等分だから1/14です。したがって答えは「半分と1/14」つまり1/2;1/14になります。

　計算表は次のようになります。4/7 を越えないもっとも大きな単位分数は 1/2 です。目標は右の欄に 4 を作ることです。1行目を2で割ると 3;1/2 ができます。4からこれを引くと 1/2 となります。3行目は1行目の〔ひっくり返し〕です。これを2で割ると 1/2 ができます。

もう一つ例題を見てみましょう。

3個のパンをそれぞれ6等分します。すると1/6のパンが18切れできます。これを16人に分けると2切れの残ります。残りをそれぞれを8等分すれば16人に分けられます。1/6の8等分は1/48ですから、答えは1/6;1/48になります。

この計算は以下のような表で計算することができます。

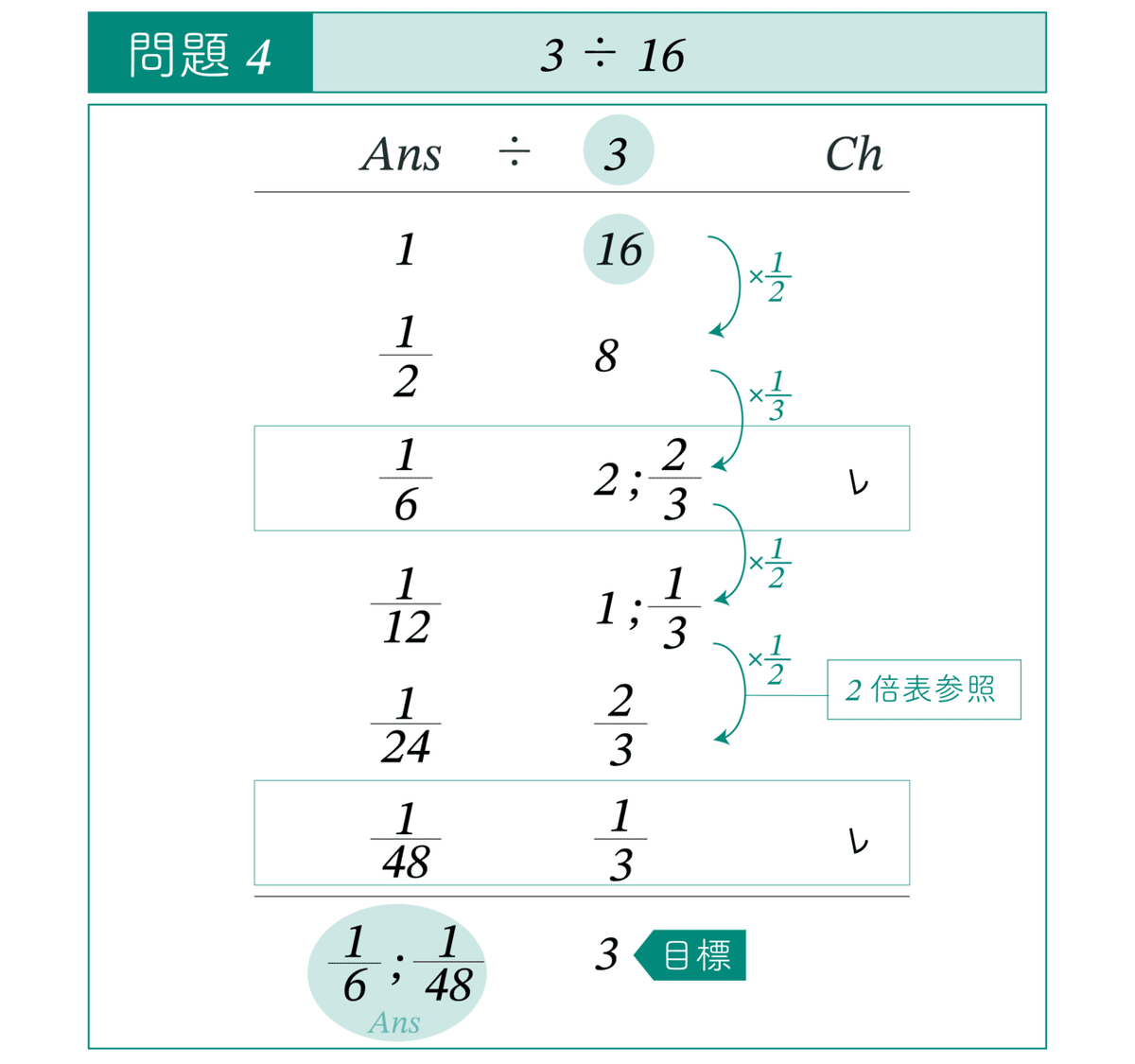
　 目標は 3 です。1/5 ＝ 3/15 は 3/16 より大きいので不適です。1/6 を作ります。1行目を2で割り、さらに3で割ると 2;2/3 が得られます。これを目標の3から引くと 1/3 が得られます。これが次の目標です。5行目は4行目を2で割っています。これは〔2倍表〕の 2/3 の欄の

を逆向きに使っています。
　16 は2の累乗の形（16＝2⁴）なので、3÷16 は2分法だけで計算でき、計算結果は 1/8;1/16 となります。古代エジプト人は、1/8;1/16 よりも 1/6;1/48 の方が“よい表現”だと思ったのでしょう。3/16 は「約 1/8」よりも「約1/6」の方が“より近い値”だからです。

　古代エジプト人はたくさんの計算をこなすうちに、様々な規則に気付き、計算方法を確立していきました。2倍法や2分法は規則的に2倍、2倍としていくだけでしたが、拡張規則を使うには、目標となる数字を作るために、より効率のよいやり方を考えて等式を使いこなさなければなりません。古代エジプト人は計算を何度も繰り返して、よりよい方法を体得していったのだと思います。

　何回かにわたり、古代エジプト算法を題材にしてかけ算や割り算のお話をしてきました。次回は割り算の概念はどのようにして生まれたのか「そもそも割り算って何だろう？」という問題について考えてみましょう。

▼ 関連記事

▼数学Webマガジン・マテマティカ 『ピラミッドの謎』

エジプトのピラミッドには多くの謎が隠されています。マテマティカのWeb連載『ピラミッドの謎』では、ピラミッドの数に関する3つの謎「円周率の謎」「黄金比の謎」「地球の緯度の謎」を取り上げます。古代エジプトの歴史やエジプト神話など、様々な角度からピラミッドの謎に迫ります！
noteの『古代エジプトの数学』シリーズで扱っている「古代エジプトの数学能力」を知ることが謎を解く鍵になります。ぜひ合わせてご覧ください。

【Web連載：ピラミッドの謎】 3-1.エジプトの数 | マテマティカ

▼Twitter、Webマガジンサイトも更新中。よろしくお願いいたします。
Twitter: @mathematicasite
Web:http://mathematica.site/