
古代エジプトではどのような方法で5個のパンを8人に分けていたか? 〜エジプト分数の考え方〜
エジプト分数とは?
古代エジプト数学の特徴の一つは、エジプト分数と呼ばれている数を用いていることです。「エジプト分数は、幼稚で制限の多い方法だ」などいう意見をこれまでよく聞きました。“数”は一度習得して慣れてしまうと異質のものはなかなか受け入れがたいものです。現代人の私たちから見れば、原始的で奇妙な方法に見えるかもしれませんが、先入観を持たずにまずよく理解することが必要です。エジプト分数はとても理にかなった記数法ですし、アルキメデスのようなヘレニズム期の数学者たちや、フィボナッチなど中世ヨーロッパの数学者もエジプト分数を用いています。まずはエジプト分数とはどのようなものかを見てみましょう。
分数というもののそもそもの始まりは単位分数です。単位分数とは、分子が 1 で分母が自然数 a の分数 1/a のことです。私たち日本人は分数 m/n を「n 分(ぶん)の m」といいますが“n 分(ぶ)”というのは「n 等分したもの」いう意味で、「n 分(ぶん)の m」は 「n等分したものが m個」、つまり「単位分数が m個」という意味なのです。日本(中国)でも、分数は単位分数から始まったのです。記法と言語は密接に関係していて、お互いに一緒になって発展してきたものと思います。
古代エジプトの記数法
エジプト分数は次の規則に従って単位分数を並べたものです。
・ 大きさの順に左から右へ並べる。2個以上の同じ単位分数が現われてはいけない。
・ 最初に1つだけ自然数を書いてもよい。自然数はなくてもよい。
・例外的に 2/3 だけは単位分数に準ずるものとして許される。
この記事の中では、エジプト分数の中で単位分数と単位分数を区切る記号としてセミコロン( ; )を使用することにします。
例えば、次の4つはエジプト分数です。

エジプト分数の表し方をまとめると以下のようになります。

もちろんこれは現在の表記方法です。古代エジプトでは神聖文字(ヒエログリフ)と呼ばれる文字が使われていました。古代エジプトの数は次のように表します。
・1から9までの数 n は | をn本並べる。
・10から90までの数 10n は ∩ をn個ならべる。
・1 / n は n の上にホルスの目を書く。
単位分数「1/n 」は n を表す神聖文字の上にホルスの目を書いて表しますので、1/4 と 1/12 は次のようになります。

パピルスの問題を考える
エジプト分数は、もともとは『ホルスの目のお話』で述べた2進分数だったのですが、上で述べた形のものは、中王国時代 (紀元前2000年頃~1700年頃) に使われ始めたようです。
出土したパピルスには「何個かのパンを何人かで等分する」という問題がいくつかあります。この問題で解きながら、古代エジプト人が分数をどのように扱っていたかを具体的に見てみましょう。

現在の私たちは直ちに「8分の5」と答えると思います。上で述べたように日本語の「8分の1」は、「8等分したもの5切れぶん」という意味です。この方法だと、それぞれのパンは8等分されてしまいます。

エジプト数学では次のように考えます。5個のパンそれぞれを半分に割ります。すると 1/2のパンが 10切れできます。これを8人に分けると、2切れ残ります。この2切れそれぞれを4つに割ります。すると 1/8のパンが8切れでき、8人に分けることができます。1人の取り分は 1/2 と 1/8、つまり 1/2;1/8 となります。

最初の方法ではパンは8等分されましたが、この方法では半分に割ったパンを分け、残りをさらに分割することで、大きな塊で分けることができます。
この考え方を使って、現在の分数をエジプト分数で表すことができます。5/8 をエジプト分数で表すには、5/8 を越えない最も大きな単位分数を見つけます。1/2 です。5/8 から 1/2 を引くと

となり、「5/8 は 1/2 とちょっと」ということがわかります。
もう一つ、別の問題を考えてみましょう。

現代人なら即座に 3/4 と答えるでしょう。しかし 3/4 はエジプト分数ではありません。古代エジプトでは次のように考えます。まず3個のパンを半分に割ります。すると 1/2 のパンが6切れできます。このうち4切れを4人に分け、残りの2切れをさらに半分に割ります。すると、1/4 が4切れできます。したがって、答えは1人 1/2;1/4個、つまり 1/2切れ1個と1/4切れ1個となります。

古代エジプト人はこれに満足しなかったようです。古代エジプトでは3という数を「神聖な数」と見ていました。1ヵ月は30日です。日本や中国では1年を“四季”に分けますが、エジプトでは“三季”に分けています。そこで次のような方法を取りました。3個のパンそれぞれを3等分すると、1/3 のパンが 9切れできます。つまり2/3 が4切れでき、1/3 が残ります。残った 1/3 をさらに4等分すると、1/12 が 4切れできます。したがって一人当たり 2/3;1/12 個となります。言いかえると、エジプト分数では「2/3 を特別扱い」しているのです。

どんな分数もエジプト分数で表すことができる
エジプト分数に関する定理として次の定理が知られています。
〔定理〕 任意の有理数はエジプト分数で表すことができる。
有理数という概念は近世になるまで現れませんから、これは現代の定理です。有理数とは分数で表わされるような数のことです。与えられた有理数を m/n とします。上で述べたように m/n に最も近い単位分数 1/q を見つけます。たとえば 5/11 で試してみましょう。11 ÷ 5 を計算すると 2.2 ですから、

となるので、5/11に最も近い単位分数は1/3であることがわかります。したがって、

となります。次は、4/33 を単位分数に分解します。33 ÷ 4 = 8.25なので4/33に最も近い単位分数は1/9になります。したがって、
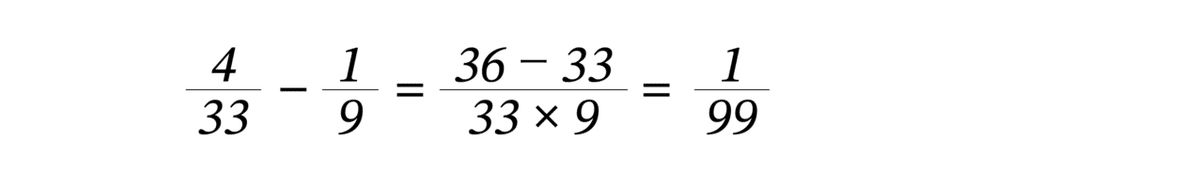
となり、5/11を以下のように単位分数に分解することができました。

この例でわかるように、最初の分子は 5/11 の 5 、次は 4/33 の 4となり、繰り返すごとに分子の数は小さくなっています。したがってこの操作は無限に繰り返されることはありません。今回この定理の証明は割愛しますが、このような考え方でどんな有理数も最終的にエジプト分数に分解することができるのです。
私達は5/11に一番近い単位分数を見つける時に電卓で「11÷5」と計算することで、簡単に答えを得ることができます。しかし古代エジプトにはもちろん電卓はありません。エジプト人は 4/33 に最も近い単位分数を 1/2, 1/3, … と順に調べていったのでしょう。
エジプト数学から“数とは何か”を学ぶ
私達は数の中で暮らしています。分数の計算は小学校で習いますので、分数は”あたりまえ”の存在になっているかもしれません。しかし分数というものはとても難しい概念で、人類がこの概念を得るまでにはとても長い年月を必要としたのです。ヨーロッパでは近世になるまで、小数はおろか分数もまともに扱われていませんでしたし、アラビアから分数や小数が入ってきてからも、これを習得するのに何百年もかかっています。エジプト分数は私たちがどのようにして分数という概念を獲得していったかを考える上で大きなヒントを与えてくれるのではないかと思います。
![]()
▼関連記事
▼数学Webマガジン・マテマティカ 『ピラミッドの謎』
エジプトのピラミッドには多くの謎が隠されています。マテマティカのWeb連載『ピラミッドの謎』では、ピラミッドの数に関する3つの謎「円周率の謎」「黄金比の謎」「地球の緯度の謎」を取り上げます。古代エジプトの歴史やエジプト神話など、様々な角度からピラミッドの謎に迫ります!
noteの『古代エジプトの数学』シリーズで扱っている「古代エジプトの数学能力」を知ることが謎を解く鍵になります。ぜひ合わせてご覧ください。
![]()
▼数学Webマガジン・マテマティカ 『数の発明』
私たち人類はいつ頃から「数」を扱うようになったのでしょうか。旧石器時代までの進化の時代、そして人類が農業というすばらしい手段を発明し、文明が興るまでの間にはどのような道のりがあったのでしょうか。人類が「数の概念」を獲得するまでの様子を見てみましょう。
▼数学Webマガジン・マテマティカ 『バビロニアの数』
皆さんは、むかし南メソポタミア地方に栄えたバビロニアという国をご存知でしょうか。最近になって太古の昔この地に高度な数学や天文学が発展していることが分かってきました。マテマティカWeb連載『 バビロニアの数 』では、60進数という記数法はどのようにして生まれたのか、バビロニアで行われていた高度な計算とはどのようなものだったのか、などバビロニア数学に焦点を当て詳しく紹介しています。ぜひご訪問ください!
▼Twitter、Webマガジンサイトも更新中。よろしくお願いいたします。
Twitter: @mathematicasite
Web:http://mathematica.site/
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?


