統計検定2級に向けて、帰無仮説と対立仮説の立て方を論理的に考えよう
はじめに
分析屋の小泉と申します。
前回の記事で振り返った基本統計量は、データの様々な側面の代表を表し、得られたデータの過去の状態を簡単に表すものです。
前回の記事はこちらです。
ただ、実際の場面では得られたデータを見てどうこう話すよりも、今後のデータがどうなるのかを考えることの方が多いです。
このとき絶対に帰無・対立仮説や有意確率という言葉が出ますが、非常にややこしく解釈も難しい。。。
統計検定3級から2級に上がるときの一番の関門ではないでしょうか。
今回は帰無仮説と対立仮説について、「なぜそんなものを立てるの？」という視点から考えていきます。
自分が勉強した際の経験などを踏まえて、その概念について親しみを持って頂ければと思います。
ちなみに今回は数式は一切出ません。ご安心ください。
命題と否定
統計学は確率を用いた主張に利用できる学問です。
確率というのは曖昧な部分もあり、主張できる範囲をよく確認していないと、説得力が失われたり粗が出てきてしまいます。
命題
主張において、真偽がはっきりと明示できるテーマを命題といいます。
今回は執筆者である私、小泉について考えてみます。
A：執筆者の小泉さんは日本人である。
B：執筆者の小泉さんは泳げない。
C：執筆者の小泉さんは2000年以降の生まれである。
A、B、Cの3つの主張がありますが、命題として定められるのはAとCのみです。
AはYes(真)かNo(偽)か明らかで、国籍という絶対的尺度に基づき、真が得られます。
Bは一見すると明らかですが、実際はクロールの息継ぎが出来ないだけのため、泳げないと言い切るには主観的すぎて根拠が足りません。だから泳げないって言わないで
Cの生まれ年は変わりようがありません。一方で、実際は1996年生まれなので、この主張は偽となります。
このように、真偽は問わず、絶対的尺度もしくは不変なものに基づいて行う主張が命題です。
命題の否定
先の命題について、もう少し論理学に適用できるように改編します。
執筆者の小泉さんは日本人である。
↓
執筆者が小泉さんならば執筆者は日本人である。
Aでは小泉さんは日本人としていますが、ならばと置くことで、
2つの関係が並行（＝）ではなく主従（→）が生まれました。
並行のままでは、前後を入れ替えても文が成立するため、論理学的に不明瞭ですからね。
主従関係なので「〇〇ならば△△」は、
「〇〇があるから△△がある」という方向になります。
ならばより前の〇〇を仮定、後の△△を結論と呼びます。
仮定と結論にはそれぞれ否定を用意することができます。
仮定：執筆者が小泉さんである（執筆者＝小泉さん）
仮定の否定：執筆者が小泉さんではない（執筆者≠小泉さん）
結論：執筆者は日本人である（執筆者＝日本人）
結論の否定：執筆者は日本人ではない（執筆者≠日本人）
単純ですが、「〜ではない」とするだけで大丈夫です。
今回は結論の否定のみを使いますが、命題の裏や逆、集合についての話もここから展開することが可能です。蛇足になるので今回は省略します。
二重否定における主張
それでは、命題の結論を否定し、更にもう一度否定したらどうなるでしょうか。
執筆者が小泉さんならば執筆者は日本人である。
↓結論の否定
執筆者が小泉さんならば執筆者は日本人ではない。
↓結論の二重否定
執筆者が小泉さんならば執筆者は日本人ではないとはいえない。
・・・いよいよ訳が分からなくなってきました。
「日本人でないとはいえないってなんだよ！つまり日本人なんだろ！」
とお怒りの方もいらっしゃることでしょう。
しかし結論が同じだとしても、命題と命題の二重否定を同列に扱うことは、論理的には好ましくありません。なぜでしょうか？
命題を証明するには、命題の否定が矛盾することを証明しなくてはならないからです。
例えば「実験データが100個ある」と主張するならば、
「実験データが100個ではない」が矛盾することを証明する必要があります。
正直ややこしいですし、文章が長くなるので実際の主張においてはあまり使いません。
ただ、厳密に定義しないと粗を探されてしまうのでこのように考えるのです。
私も日常会話でここまで長く話すことはしませんが、この考え方に慣れてくださいね。
帰無仮説と対立仮説
さて、それでは帰無仮説と対立仮説について考えます。
次のようなテーマと検証方法、仮説を考えてみましょう。
テーマ： すべてのカラスは黒いのか？
検証方法： 東京23区内のランダムに選出された10の公園でカラスを1匹捕獲し、色を確認する
仮説： 東京23区内のカラス（8328羽、令和5年のデータ）の色は黒である
ありがちなランダムサンプリングでのフィールド調査ですね。
サンプリング方法やサンプリング数は検討の余地がありますが、今回は重要ではないので省きます。
さて、検証の結果が出ました。
黒が9羽、白が1羽でした。
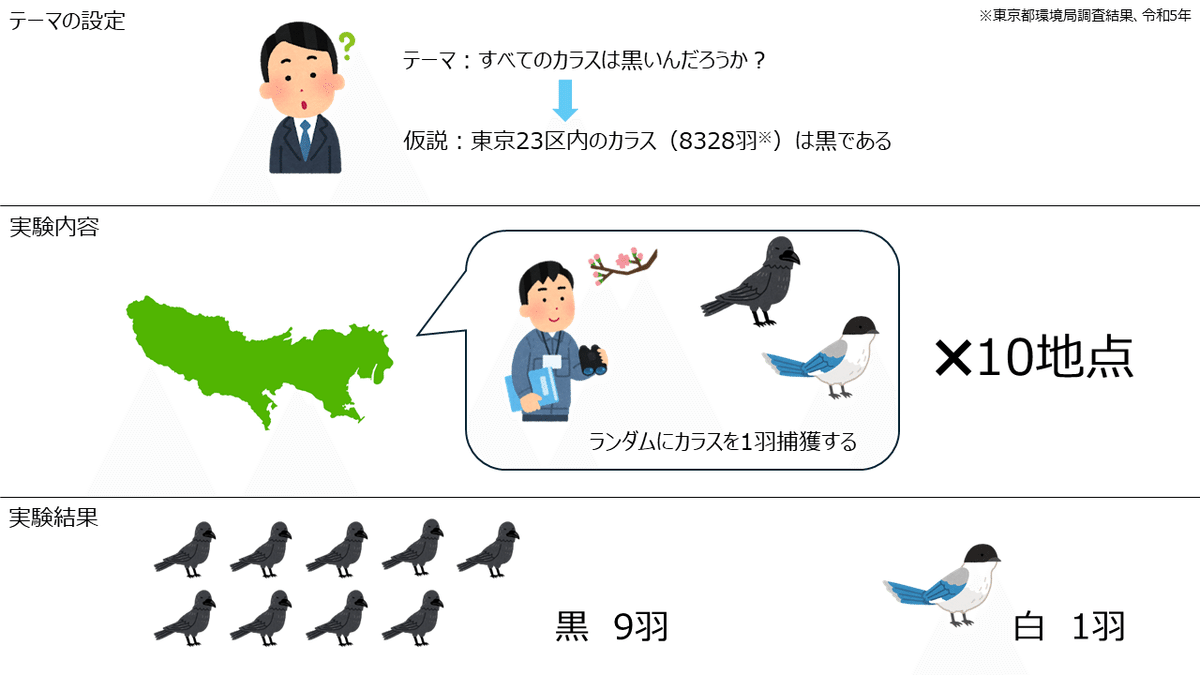
・・・さて、この結果から、仮説を支持すべきでしょうか？
「結果の90%は黒であるから、大体は合ってるんじゃない？」と言えるかもしれません。
しかし、一部の人はこう考えるかもしれません。
「白いカラスはどこかに偏ってもっといるかもしれない！」
「10%が白ってことは全体で白が830羽もいるの！？黒とは言い切れなくない？」
こう言われてしまうと、反論出来るでしょうか？
では、仮説だけをこのように変えて実験結果を捉えてみましょう。
仮説： 東京23区内のカラスの色は黒ではない
この仮説の上で、黒が9羽、白が1羽という結果を得るとどうでしょうか。
「白いカラスが10%しかいない！90%は仮説にそぐわない結果になっているじゃないか！」
「ほとんどのカラスの色は黒じゃないか！そんな仮定はさすがに嘘だろ！」
このように考える人が多いのではないでしょうか。
もちろん、
「たまたま9匹が黒かっただけで、白いカラスは一部に密集してて数も多いはずだ！」と反論もできます。
ただ、10の地点のうち9の地点で黒いカラスが捕れたんですから、なかなか説得力が弱いような気がします。
少なくとも、10の地点のうち1の地点でしか白いカラスが捕れなかったのに、カラスは黒くないと断定するのはちょっとナンセンスですよね。
これにより、
「黒ではない」という仮説を棄却し、「黒である」という仮説を支持する方が矛盾が少ないという主張が形成できました。
本来の主張（テーマ）と対立する仮説をわざと提起するのは、前述の命題の否定と繋がりますね。
このように、提起された仮説に対して、わざと対立する仮説を対立仮説といいます。
一方で、対立仮説を棄却したときの結論を考えてみましょう。
「カラスは黒くない」という仮説を棄却することで得られるのは、
「カラスは黒くないとはいえない」ということでしかありません。
特に今回の場合、最初の仮説は肯定も否定も難しいです。
もしかしたら白いカラスは偏っていてどこかに多数存在するかもしれません。
黒であるという保証はどこにもなく、断定もできないのです。
最初の仮説と対立仮説を用意して、
どちらを支持/棄却する方が矛盾が少ないかを争わせます。
しかしながら、最初の仮説を支持したところで結論は断定できません。
すなわち、結論が【無】に【帰す】仮説なので、帰無仮説と言います。
これが、帰無仮説と対立仮説を立て、結論まで行う流れになります。
今回ですと、以下のようになりました。
帰無仮説：東京23区内のカラスは黒である
対立仮説：東京23区内のカラスは黒ではない
今回は感覚でどちらを支持するか決めましたが、
今後はt検定やF検定などによってp値を算出し、（ある程度）定量的に判断していくことになります。
まずはロジックに慣れていきましょう。
帰無仮説と背理法、有意確率（余談）
さて、ここからは余談です。
統計検定2級取得だけならあまり深く考えなくてよい話ですが、
データサイエンスに関わる者としてこれに触れないわけにはいきません。
対立する仮説を立て、それを棄却することで元の命題を証明することを、論理学的には背理法と言います。
統計学においても、例えば無相関の検定で利用するロジックです。
対立仮説の棄却は、論理的には背理法と同じです。
しかし、帰無仮説・対立仮説どちらを棄却/採択しても、結論が断定できないことが明確に異なります。
統計的検定・推定に慣れてくると、流れ作業のように「p値≧0.05かー、じゃあ対立仮説を棄却して帰無仮説で結論作ろう」となることが多くなります。
一般的に説得・弁論で使う分にはそこまで支障はありませんが…
忘れてほしくないのは、「結論が無に帰すから帰無仮説」なのであり、「統計的有意差がない」ことの証明ではないのです。
対立仮説が支持されたとしても、それは分析者の理想に沿った結果に近いかもしれないという話でしかありません。
もう少し詳細に説明すると、
分析者には「こうだったら嬉しい」「おそらくこの分布に従う」という理想モデルが存在します。
有意確率とは、もう一つデータを取ってきたときに理想モデルに従う確率であり、そこから結論を導くために帰無仮説と対立仮説を立てているに過ぎません。
今回の例では「一般的に考えてカラスは黒でしょ？」という認識が理想モデルに当たり、
「次にどこかでカラスを捕獲したら、カラスが黒でない確率が低いだろうな」という有意確率から、対立仮説を棄却した方がいいよねという主張をしています。
統計学に慣れてきたら、このような理想モデルへのバイアスを考慮し、次の2点に注意しましょう。
本当に意味のある検定・推定なのか？
この有意確率・仮説の棄却に意味があるのか？
特に、データ数が少なく信頼性に欠ける場合はよーーーく再検討しましょう。
米国統計学会(ASA)がこれについて声明を出していますので、余談です。
excelやR、pythonで検定推定は非常に簡単にできますが、その簡便さに甘えすぎないようにしましょう。
生成AIでいうハルシネーションを、人間が意識せずにやってしまわないように。。。
おわりに
今回は帰無仮説と対立仮説についての解説でした。
自分が初めてこれに触れたときに全く理解が出来なかったため、
論述の面からじっくりと解説したつもりでしたが、少しでも理解の助けになれば幸いです。
なお、帰無仮説も対立仮説も、本来は終盤に登場した有意確率（p値）が前提にあります。
ただし統計モデルや分布の理解を深める必要があり、一本の記事には出来ないため、またの機会に譲ります。
同じことを言ってるはずなのに、印象とか見方を変えれば説得力が変わるというのは、実務においてもよくある話です。
このようにわざと反論から主張を引き出すというのは様々なことに応用できますので、是非身につけてみてください。
参考文献
・統計学入門（基礎統計学Ⅰ）、東京大学教養学部統計学教室編集
・入門統計解析法、永田 靖 著
・AMERICAN STATISTICAL ASSOCIATION RELEASES STATEMENT ON STATISTICAL SIGNIFICANCE AND P-VALUES
・統計的有意性とP値に関するASA声明、日本計量生物学会国際担当理事 佐藤 俊哉 著
ここまでお読みいただき、ありがとうございました！
この記事が少しでも参考になりましたら「スキ」を押していただけると幸いです！
株式会社分析屋について
弊社が作成を行いました分析レポートを、鎌倉市観光協会様HPに掲載いただきました。
ホームページはこちら。
noteでの会社紹介記事はこちら。
【データ分析で日本を豊かに】
分析屋はシステム分野・ライフサイエンス分野・マーケティング分野の知見を生かし、多種多様な分野の企業様のデータ分析のご支援をさせていただいております。 「あなたの問題解決をする」をモットーに、お客様の抱える課題にあわせた解析・分析手法を用いて、問題解決へのお手伝いをいたします！
【マーケティング】
マーケティング戦略上の目的に向けて、各種のデータ統合及び加工ならびにPDCAサイクル運用全般を支援や高度なデータ分析技術により複雑な課題解決に向けての分析サービスを提供いたします。
【システム】
アプリケーション開発やデータベース構築、WEBサイト構築、運用保守業務などお客様の問題やご要望に沿ってご支援いたします。
【ライフサイエンス】
機械学習や各種アルゴリズムなどの解析アルゴリズム開発サービスを提供いたします。過去には医療系のバイタルデータを扱った解析が主でしたが、今後はそれらで培った経験・技術を工業など他の分野の企業様の問題解決にも役立てていく方針です。
【SES】
SESサービスも行っております。