トップレベル大学受験物理[1]等加速度運動

Oxford大出身生が高校物理について数学で理解する方法を解説します。
高校物理を公式暗記で解くのはナンセンスです。物理は楽しいサイエンス研究の世界への入り口。過去の科学者がしてきたように、世の中の物理現象について数学で理解を深めていきましょう。数学で理解する癖をつければ、難関大の問題程解きやすくなり、物理で高得点を狙うことができます。本シリーズを終えるころには、大学入試は東大・京大レベルでも必ず簡単に解けるようになります。

”トップレベル大学受験物理”シリーズでは、高校物理の単元ごとに分けて、入試問題も交え、原理原則を数学で理解できるよう解説していきます。今回は[1]として等加速度運動を取り上げます。物理で今後よく使う微分積分についても、初めての方にわかるよう説明していますので、ご参考ください。

---

また本記事は有料としていますが、

記事を購入していただいた方には、

トップレベル大学受験物理シリーズで解説してほしい入試問題

を募集します。

コメント、Twitterなどから、解いてほしい問題をどんどんお送りください！

有料公開範囲になりますが、随時解説をアップいたします。

---

Oxford式高校物理[1]　等加速度運動
Oxford式高校物理[2]　運動方程式
Oxford式高校物理[2-Appendix]　極座標の運動方程式
Oxford式高校物理[3]　エネルギー保存
Oxford式高校物理[4]　運動量保存

速度、加速度と微分

図１

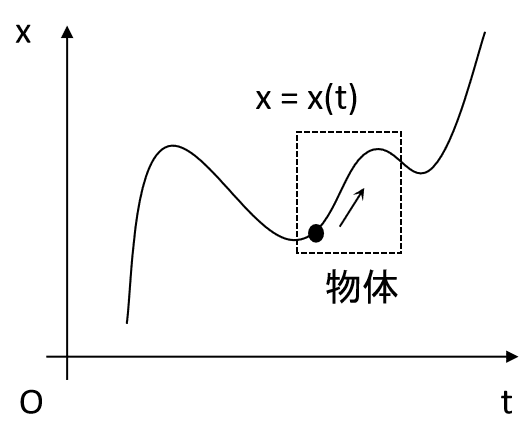
図１のように、物体（質点）が時間tに対して1次元空間を移動しているとする。このとき、物体の位置xは時間tの関数として、

$$
x = x(t)
$$

などと、表現できる。例えば、$${ x(t) = t^2 }$$と表現される場合、$${ t= t+1 }$$における物体の位置$${x(t)}$$は、

$$
x(t+1) = (t+1)^2
$$

と表される。図１の四角部分を拡大した図を図２に示す。

図２

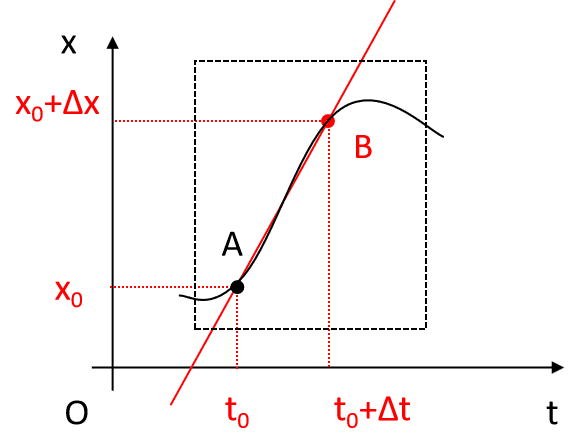
図２のように、$${x-t}$$ グラフ内に表した、$${ x = x(t) }$$上の2点、$${A(t_{0}, x_{0}) }$$, $${ B(t_{0} + \Delta t, x_{0} + \Delta x) }$$を考える。この2点ABを結ぶ直線の傾きは、

$$
\frac{x_{0}+\Delta x - x_{0}}{t_{0}+\Delta t - t_{0}} = \frac{\Delta x}{\Delta t}
$$

また、

$$
\Delta x = \frac{\Delta x}{\Delta t} \cdot \Delta t
$$

図３

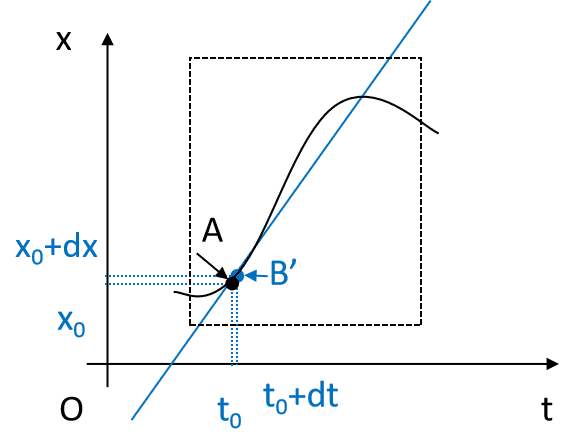
点Bが限りなく点Aに近づくとき（図３）、$${\Delta x, \Delta t}$$はそれぞれ微小変化分（微分）として、$${dx, dt}$$と表される。またこの時の直線ABの傾きについては、$${\frac{dx}{dt}}$$と定義される。すなわち、

$$
dx=\frac{dx}{dt} \cdot dt
$$

この時の$${\frac{dx}{dt}}$$を点Aにおける微分係数と呼ぶ。点Aにおける微分係数は、曲線$${x=x(t)}$$の点Aにおける接線の傾きである。また、$${x=x(t)}$$は、物体の位置座標の変化を表しており、$${\frac{dx}{dt}}$$は点Aにおける位置の瞬間的な変化、すなわち速度を表している。速度（velocity）を$${v}$$と一般的に表し、$${t=t}$$における速度$${v(t)}$$は、

$$
v(t) = \frac{dx}{dt}
$$

となる。

【例題１－１】
１）　点$${A(1,2)}$$における$${x=x(t)=2t}$$の微分係数
２）　物体が$${x=x(t)=t^2+1}$$のように時間$${t}$$に対して運動しているとき、$${t=1}$$秒後の速度$${v}$$
３）　物体が$${x=x(t)=4t^2-2t}$$のように時間$${t}$$に対して運動しているとき、$${t=1}$$秒後の速度$${v}$$

１）

$$
\frac{dx(t)}{dt} = \frac{x(t+dt)-x(t)}{(t+dt)-t} = \frac{2(t+dt) - 2t}{(t+dt) - t} = \frac{2dt}{dt} = 2
$$

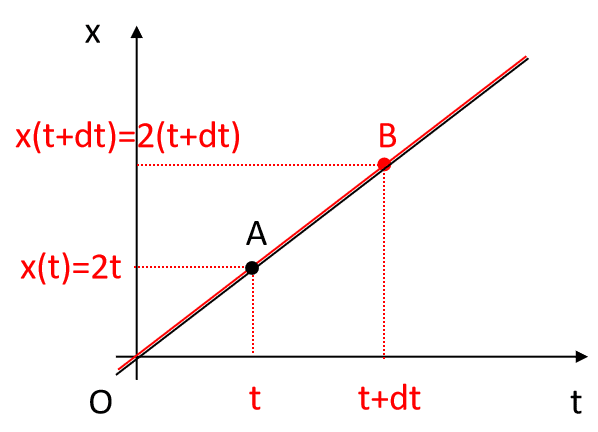
より、$${x(t)}$$の微分係数は$${t}$$の値によらず、$${2}$$となる。図４に示す通り、$${x=x(t)}$$のグラフは直線であり、$${t}$$はどんな値であっても、$${(t,x(t))}$$における接線の傾きはこの直線と同じく$${2}$$であることがわかる。上記式、また以上から、点Aにおける微分係数は$${2}$$。

図４

２）$${t=1}$$秒後の速度$${v}$$は、$${t=1}$$における$${x(t)}$$の微分係数。まず$${v(t)}$$すなわち、$${x(t)}$$の微分係数を求める。

$$
\begin{align*}
 v(t) &= \frac{dx(t)}{dt} \\ 
&= \frac{x(t+dt)-x(t)}{(t+dt)-t} \\
&= \frac{(t+dt)^2+1-(t^2+1)}{t+dt-t} \\
&= \frac{t^2 + 2 t \cdot dt + dt^2 +1 - t^2 - 1}{dt} \\
&= \frac{2 t \cdot dt + dt^2}{dt} \\
&= 2t + dt
\end{align*}
$$

ここで、$${dt}$$は$${2t}$$に比べ微小なので、$${v(t)=2t}$$と近似できる。よって$${t=1}$$における$${x(t)}$$の微分係数は、$${v(t)}$$に$${t=1}$$を代入し、

$$
v(1) = 2 \cdot 1 = 2
$$

３）２）と同様に、

$$
\begin{align*}
 v(t) &= \frac{dx(t)}{dt} \\
&= \frac{x(t+dt)-x(t)}{(t+dt)-t} \\
&= \frac{4(t+dt)^2-2(t+dt)-(4t^2-2t)}{t+dt-t} \\
&= \frac{4t^2 + 8 t \cdot dt + 4dt^2 - 2t - 2dt - 4t^2 + 2t}{dt} \\
&= \frac{8 t \cdot dt - 2dt + 4dt^2}{dt} \\
&= 8t - 2 + dt
\end{align*}
$$

ここで、$${dt}$$は他の項に比べ微小なので、$${v(t)=8t-2}$$と近似できる。よって$${t=1}$$における$${x(t)}$$の微分係数は、$${v(t)}$$に$${t=1}$$を代入し、

$$
v(1) = 8 \cdot 1 - 2= 6
$$

２）や３）のように速度$${v}$$がさらに$${t}$$により変化する場合、速度$${v}$$の微分係数$${\frac{dv(t)}{dt}}$$を

$$
a(t) = \frac{dv(t)}{dt}
$$

と表し、加速度(acceleration)と呼ぶ。速度が$${t}$$によらず一定の場合（上の１）の例）、物体は等速運動、加速度が一定の場合、等加速度運動をしているという。ちなみに、上の２）、３）の加速度はそれぞれ、

$$
\begin{align*}
a(t) &= \frac{dv(t)}{dt} \\
& = \frac{v(t+dt) - v(t)}{t+dt-t} \\
& = \frac{2(t+dt) - 2(t)}{dt} \\
& = 2
\end{align*}
$$

$$
\begin{align*}
a(t) &= \frac{dv(t)}{dt} \\
& = \frac{v(t+dt) - v(t)}{t+dt-t} \\
& = \frac{8(t+dt)-2 - (8t -2)}{dt} \\
& = 8
\end{align*}
$$

となり、いずれも等加速度運動であることがわかる。
また、$${a(t)}$$は、$${x(t)}$$を$${t}$$で2回微分していることになり、

$$
a(t)=\frac{dv(t)}{dt}=\frac{d^2 x(t)}{dt^2}
$$

と表し、$${x(t)}$$の2階微分と呼ぶ。$${\frac{dx}{dt}, \frac{d^2 x}{dt^2}}$$は、簡略化して、$${\dot{x}, \ddot{x}}$$とも表し、以降では主にこの表し方で微分係数を記載する。
物体が2次元、3次元（$${x,y}$$平面、$${x,y,z}$$空間）を運動する場合は、後述の問題解説のように、それぞれの成分について独立して加速度、速度をおいて考える。