トップレベル大学受験物理[3]エネルギー保存

[2]章ではニュートンによる運動の法則をもとに、
運動方程式の立て方について解説しました。

[3][4]章では、運動方程式をもとに、エネルギー保存、運動量保存を
立式化し、同様に入試問題をもとに、
様々な物理現象を解いていきたいと思います。

当記事での手法に慣れれば、

・何のエネルギーを考えればいいかわからない
・仕事の向きがわからない
・運動量の方向がわからない

といった不安はなくなるはずです。

---

また本記事は有料としていますが、

記事を購入していただいた方には、

トップレベル大学受験物理シリーズで解説してほしい入試問題

を募集します。

コメント、Twitterなどから、解いてほしい問題をどんどんお送りください！

有料公開範囲になりますが、随時解説をアップいたします。

---

運動方程式からエネルギー保存則を導こう

【例題１】
下図のような高さ$${h}$$から自由落下する（初速$${t=0}$$で$${v_0=0}$$）質量$${m}$$の質点を考える（重力加速度：$${g}$$）。この質点の力学的エネルギー保存則から、地表面付近まで落下した際の、質点の速度$${v}$$を求めよ（空気抵抗等は無視し、質点にはたらく力は重力のみとする）。

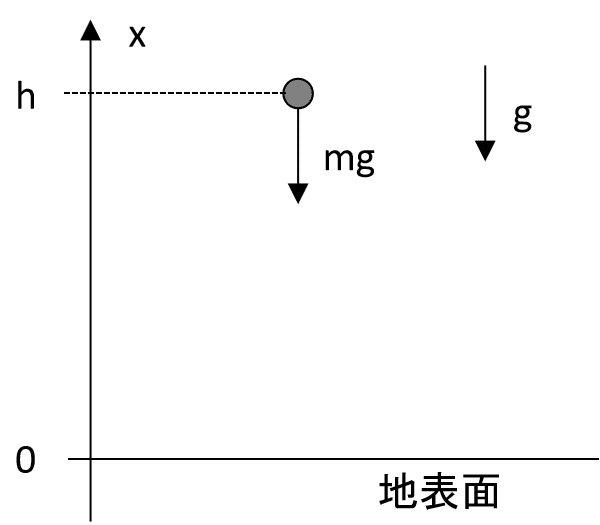
地表面から上向きに$${x}$$軸をとり、質点の座標を$${x}$$とすると、質点についての運動方程式は、

$$
m\ddot{x} = -mg ----(ex1.1)
$$

となります。$${(ex1.1)}$$の両辺に$${\dot{x}}$$をかけると、

$$
m\ddot{x}\dot{x} = -mg\dot{x} ----(ex1.2)
$$

となります。ここで、$${\dot{x}=v}$$としたとき、$${v^2}$$を時間微分すると、

$$
\frac{d}{dt}v^2 = \frac{d}{dv}v^2 \cdot \frac{dv}{dt}=2v\dot{v}(=2\dot{x}\ddot{x}) \\
つまり、d(v^2) = 2v\dot{v}dt \\
\therefore \int d(v^2) (= v^2) = \int 2v\dot{v}dt
$$

と変形できます。式$${(ex1.2)}$$を変形し、両辺を$${t}$$で積分すると、

$$
m\ddot{x}\dot{x} + mg\dot{x} = 0 -----(ex1.3)\\
\int (m\ddot{x}\dot{x} + mg\dot{x})dt =  const. \\
\therefore \frac{1}{2}m\dot{x}^2 + mgx = const. -----(ex1.4)
$$

$${const.}$$は一定という意味で、$${(ex1.4)}$$の左辺が、時間によらず一定の値をとる、という意味です。$${(ex1.4)}$$の左辺を力学的エネルギーと呼び、この式を力学的エネルギー保存則と呼びます。力学的エネルギーのうち、第１項の$${\frac{1}{2}m\dot{x}^2}$$を運動エネルギー、第２項の$${mgx}$$を重力による位置エネルギーと呼びます。

$${x=0}$$と$${x=h}$$での力学的エネルギーは保存されるので、$${(ex1.4)}$$から、

$$
\frac{1}{2}mv^2 + mg\cdot 0 = \frac{1}{2}m \cdot 0^2 + mg \cdot h ----(ex1.5)\\
\therefore v=-\sqrt{2gh} （衝突時、速度は下向き）
$$

として、衝突時の速度を求めることができます。また、$${(ex1.3)}$$の両辺を$${t=0}$$から衝突時$${t=t_1}$$まで積分すると、

$$
\int_0^{t_1} (m\ddot{x}\dot{x} + mg\dot{x})dt = 0 \\
\therefore (\frac{1}{2}mv^2 + mg\cdot 0) - (\frac{1}{2}m \cdot 0^2 + mgh) = 0 \\
\therefore \frac{1}{2}mv^2 + mg\cdot 0 = \frac{1}{2}m \cdot 0^2 + mg \cdot h ----(ex1.5)
$$

のように、$${(ex1.5)}$$と同様の式を得ることができます。

このように、エネルギー保存の問題であっても、運動方程式さえ立式できれば、数学的に保存則を導出することができ、エネルギーの増減で悩む必要はありません。

実際の入試問題で、運動方程式からエネルギー保存則を導出して考えてみましょう。