一級建築士学科試験で学ぶ「黄金比」について、知らないと諦めず、数学的に解いてみよう

黄金比は、線分ＡＢ上に点ＰをとってＡＰ×ＡＢ＝ＰＢ2となるときのＡＰ：ＰＢをいい、その比は約1：1.414であり、モデュロールに応用されている。
　　　　　
　以上、平成27年一級建築士学科試験問題　
　　学科Ⅰ（計画）〔No.７〕
　　　選択肢２．の記述（不適当なもの）より

　　　　✳ＰＢ2：ＰＢ２乗（ＰＢ×ＰＢ）

＜解き方・考え方①＞
　黄金比を知っている場合
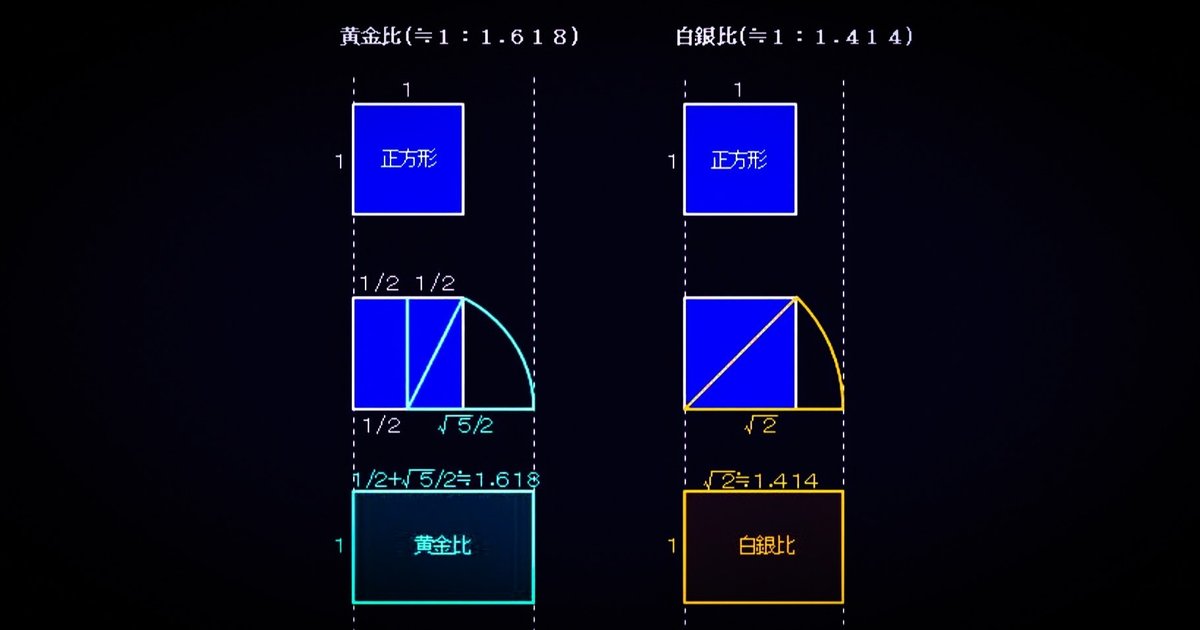
・黄金比は約1：1.618であり、記述は不適当。
　（見出し画像参照）

＜解き方・考え方②＞
　白銀比を知っている場合
・約1：1.414は白銀比であり、記述は不適当。
　（見出し画像参照）

＜解き方・考え方③＞
　フィボナッチ数列と黄金比の関係を知っている場合
・1、1、2、3、5、8、13、21、…
　Ｎ1、Ｎ2、Ｎ3、…とした場合、
　Ｎ3＝Ｎ1＋Ｎ2のように、前の２つの数字を足したものが次の数字になり、これを繰り返しながら続いていくのが、フィボナッチ数列です。
　上の21の次に続く数字は、13＋21＝34になるということです。
　3／2＝1.500
　5／3≒1.666
　8／5＝1.600
　13／8≒1.625
　21／13≒1.615
　34／21≒1.619
　といったように、フィボナッチ数列の前後隣り合う２つの数字の比は、黄金比に近づいていきます。
　上のように一定のルールのもと、フィボナッチ数列を再現していくこと自体は難しくはないので、適当なところで前後隣り合う２つの数字の比を出せば、
約1：1.414が、黄金比ではないことがわかり、記述は不適当となります。

＜解き方・考え方④＞
　問題の記述の矛盾を数学的に証明してみる場合
・問題の記述より
　Ａ－ 1 －Ｐ－－1.414－－Ｂ
　　ＡＰ＝1
　　ＰＢ＝1.414
　　ＡＢ＝ＡＰ＋ＰＢ＝1+1.414＝2.414
　よって
　　ＡＰ×ＡＢ＝1×2.414＝2.414
　　ＰＢ2＝ＰＢ×ＰＢ＝1.414×1.414≒  2　
　　∴ＡＰ×ＡＢ≠ＰＢ2
　上により、問題の記述は成立していないと結論づけることができます。黄金比が何なのかを知らなくても、数学的に解いてみると、不適当な記述だと判断できるということになります。
　ちなみに、上式の1.414を1.618（≒1/2+√5/2）に置き換えると問題の記述が成立することがわかります。　

　以上のように、問題の記述の正誤判別をするに当たり、いくつかの＜解き方・考え方＞ができる場合があります。　
　記述を読んで、即、「知らない」「わからない」と結論づけずに、解く手がかりを頭の中で検索することを習慣づけ、思考のトレーニングをしていくことも、試験対策として必要だと思っています。

建築士の塾 by archicom