【東京大学2021年度入試数学(理系)第4問】解答の難しい整数問題

今回は2021を盛り込んだ整数問題です。今年出題された6問の中でも最も面白い問題です。

東京大学　安田講堂
2016年12月24日、 Kakidai撮影、Wikipediaより

問題

以下の問いに答えよ。

(1) 正の奇数 K, L と正の整数 A, B が KA = LB を満たしているとする。K を 4 で割った余りが L を 4 で割った余りに等しいならば，A を 4 で割った余りは B を 4 で割った余りと等しいことを示せ。

(2) 正の整数 a, b が a > b を満たしているとする。このとき，A = (4a+1)C(4b+1), B = aCb に対して KA = LB となるような正の整数 K, L が存在することを示せ。

(3) a, b は (2) の通りとし，さらに a - b が 2 の倍数で割り切れるとする。(4a+1)C(4b+1) を 4 で割った余りは aCb を 4 で割った余りと等しいことを示せ。

(4) 2021C37 を4 で割った余りを求めよ。

解答解説

この問題は誘導問題が良く設計されています。多分、一番面倒な問題であったと思います。が、私はこういう問題の方が得意なので、戦略はすぐにたちました。とはいえ、解答を書くとなると話は別です。

実際、(2) と (3) については長くなってしまったために解答を書き換えました。(オリジナルは感想の後に載せています。)

(1) は素直に考えてみましょう。K, L を 4 で割った商をそれぞれ p, qと、共通の余りを r とおくと、
・K = 4p + r
・L = 4q + r
と表すことができます。ここで、K と L は奇数であり、r は K, L を 4 で割った余りであるので、r = 1 もしくは r = 3 となります。

KA = LB より、(4p + r)A = (4q + r)B すなわち r(A - B) = 4(qB - pA) となりますが、p, q, r, A, B は全て整数であることから、右辺は 4 の倍数で、r と 4 は互いに素であるので、A - B は4の倍数となります。

すなわち、A を 4 で割った余りと B を 4 で割った余りは等しいことが証明されました。

(2) は、(4a+1)C(4b+1) を式変形していきます。

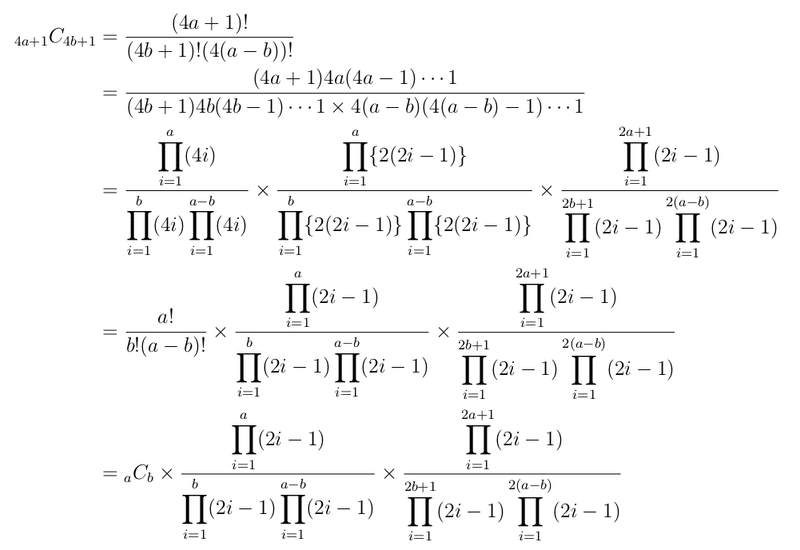
ここで、Π という見慣れぬ記号が出てきますが、これは Σ の掛け算版です。この方が書くのが簡単で、どのように分子分母を分けたかが分かりやすいので使いました。

上の式は要するに、分子分母にある因数(掛け算の構成要素)を「4の倍数」「4の倍数ではない偶数」「奇数」に分けて、4の倍数同士を4で、4の倍数ではない偶数同志を2で約分しています。

これにより、

とおくと、K と L はそれぞれ奇数であり、上式より KA = LB が成立するのは明らかなので、これが条件を満たす K と L になります。

(3) は、K を 4 で割った余りと L を 4 で割った余りが等しければ、(1) より命題が成立することになります。

m, n が整数であるとき、
・(4m + 1)(4n + 1) = 4(4mn + m + n) + 1
・(4m + 1)(4n + 3) = 4(4mn + 3m + n) + 3
・(4m + 3)(4n + 3) = 4(4mn + 3m + 3n + 2) + 1
であることから、奇数のみからなる積は、そこに含まれる4で割って3余る因数の個数が偶数のときは 4 で割って 1 余り、4で割って3余る因数の個数が奇数のときは 4 で割って 3 余ります。

よって、K に含まれる 4 で割って 3 余る因数の個数と L に含まれる 4 で割って 3 余る因数の個数の偶奇が等しいことを証明すれば十分となります。

では、K と L の因数の中に4で割って 3 余る数が何個あるかを数えましょう。

1, 3, 5, 7, ... を 4 で割った余りは 1, 3, 1, 3, ... と交互に現れることから、自然数 n に対して 1, 3, ..., 2n-1 の中には 4 で割って 3 余る数が [n/2] 個存在します。ここで、[x] は x を超えない最大の整数を表します。

以上のことから、4で割って3余る数は
・1, 3, ..., 2b - 1 の中には [b/2] 個
・1, 3, ..., 2(a-b) - 1 の中には [(a-b)/2] = (a-b)/2個 (a-b は2の倍数より)
・1, 3, ..., 4b + 1 の中には [(2b + 1)/2] = b個
・1, 3, ..., 4(a-b) - 1 の中には [2(a-b)/2] = a-b個
・1, 3, ..., 2a - 1 の中には [a/2]個
・1, 3, ..., 4a + 1 の中には [(2a + 1)/2] = a個
存在することになります。

したがって、
・K の中の 4で割って 3 余る因数の個数 M=[b/2] + (a-b)/2 + b + (a-b)
・L の中の 4で割って 3 余る因数の個数 N=[a/2] + a
となるので、N - M = [a/2] - [b/2] - (a-b)/2 となります。

ここで、a - b は2の倍数であることより、a と b の偶奇は一致するため、[a/2] - [b/2] = (a-b)/2 となります。したがって、N - M = 0 すなわち M = N となり、もちろん、M と N の偶奇も一致したため、命題が証明されました。

(注) M と N は、因数のとり方で4で割って3余る因数の個数そのものは変わりますが、その偶奇までは変化しないので、証明に問題は生じません。この点についてどこまで記述するかは悩ましいところです。

(4) は単に計算問題です。

2021C37 ≡ (4×505+1)C(4×9+1) ≡ 505C9 ≡ (4×126+1)C(4×2+1)≡126C2 = 126×125 ÷ 2 ≡ 3 × 1 ≡ 3 (mod 4) であるので、余りは 3 となります。

感想

(2) と (3) は当初の証明から変更しました。アイデアは同じですが、上記のように K と L を直接求める方が記述が簡単になるからです。

ですが、当初の証明の方が私の思考が伝わると思うので、かなり恥ずかしい代物ですが敢えて残しておきます。

しかし、この問題は入試としてはかなりタフだと思います。特に (3) は時間内で解くのが厳しい。(1), (2), (4) くらいが限界のような気がします。

問題としてはなかなかに意欲的で、面白い問題だと思います。少し泥臭いことを要求しますが、このくらいはありだと思いますし、それほど汚い感じはしませんでした。

別解(当初の証明)

(2) は 因数として 2 をいくつ持つかを数えれば終わりです。
・A = (2^m) L
・B = (2^n) K
と表すとします。ここで、m, n は非負整数で、L, K は正の奇数であるとします。このとき、m = n が成立すれば KA = LB = (2^n)KL が成り立つので、以下では A と B に含まれる 因数 2 の個数が等しいことを示します。

自然数 n に対して n! に含まれる因数 2 の個数を Z(n) とします。このとき、次のことが成り立ちます。

[補題1] Z(2n+1) = Z(2n) = Z(n) + n

[補題1の証明] 2n + 1 は奇数であるので、Z(2n+1) = Z(2n) は明らかです。1, 2, ..., 2n の中で因数2 を含むのは偶数である 2, 4, ..., 2n のみで、これらすべてを 2 で割ると 1, 2, ..., n が得られます。したがって、1 ～ n までの中に含まれる因数 2 の個数 Z(n) に、各偶数から 1 個ずつ取り除いた因数 2 の個数の合計 n を加えた数が Z(2n) になります。[証明終]

ここで、
・A = (4a+1)C(4b+1) = (4a+1)!/{(4b+1)! × {4(a-b)}!}
・B = aCb = a!/(b!×(a-b)!)
であるので、A に含まれる因数2の個数は m = Z(4a+1) - Z(4b+1) - Z(4(a-b))、B に含まれる因数2の個数は n = Z(a) - Z(b) - Z(a-b) となりますが、補題1より
・Z(4a+1) = Z(2a) + 2a = Z(a) + 3a
・Z(4b+1) = Z(b) + 3b
・Z(4(a-b))=Z(a-b) - 3(a-b)
であるので、m = Z(4a+1) - Z(4b+1) - Z(4(a-b)) = Z(a) + 3a - Z(b) - 3b - Z(a-b) - 3(a-b) = Z(a) - Z(b) - Z(a-b) = n が成立し、m = n が証明されました。

(2) により、A = 2^n L　かつ B = 2^n K であることが示されたので、(3) ではL に含まれる (A に含まれる) 因数で 4 で割って 3 余る数の個数と、K に含まれる(B に含まれる) 因数で 4 で割って 3 余る数の個数を数えます。ただし、その偶奇だけが等しければ十分です。

というのも、2つの奇数をかけるとき、4 で割った余りの組合せは (1,1), (1,3), (3,1), (3,3) の4通りありますが、その結果、(1, 1) と (3, 3) のときは積を 4 で割ると余りが 1 となり、(3, 1) と (1, 3) のときは積を 4 で割ると余りが 3 となります。

ということは、奇数因数の積を4で割るとき、4で割って余りが3 である因数が偶数個であれば 余りが1に、奇数個であれば余りが3になります。また、割り算に関しても同様です。

(2) と同じように、n! に含まれる4で割って3余る奇数因数の個数の偶奇を X(n) で表します。このとき、次の性質が成り立ちます。

[補題2] 任意の正の整数 n に対して
・X(2n) = {X(n) + [n/2]} mod 2
・X(2n+1) = {X(n) + [(n+1)/2]} mod 2
ここで、[x] は x を超えない最大の整数とします。

[補題2の証明] 1, 2, ..., 2n を偶奇で分けます。

偶数部分 2, 4, ..., 2n に含まれる奇数因数は、これらを2で割った 1, 2, ... ,n に含まれる奇数因数と同一であるため、この中で 4で割って3余る奇数因数の個数の偶奇はX(n) に等しくなります。

一方、奇数部分 1, 3, ..., 2n -1 は 4 で割ると 1, 3, 1, 3, ... となるので、余りが3 となる個数は [n/2] となります。よって、X(2n) の式は正しいことが示されました。X(2n+1) も同様です。[証明終]

これにより、
・X(4a+1) = {X(2a) + [(2a+2)/2]} mod 2 = {X(a) + [a/2] + a + 1} mod 2
・X(4b+1) = {X(b) + [b/2] + b + 1} mod 2
・X(4(a-b)) = {X(2(a-b)) + (a-b)} mod 2 = {X(a-b) + [(a-b)/2] + (a-b)} mod 2
となります。

さて、これらをすべて足します。{X(4a+1) + X(4b+1) + X(4(a-b))} mod 2 = {X(4a+1) - X(4b+1) - X(4(a-b))} mod 2 であるので、{X(4a+1) - X(4b+1) - X(4(a-b))} mod 2 を計算します。

{X(4a+1) - X(4b+1) - X(4(a-b))} mod 2 = {X(a) - X(b) - X(a-b) + [a/2] - [b/2] - [(a-b)/2] } mod 2

ここで、a-b が2の倍数であるので、[a/2] - [b/2] = (a-b)/2かつ[(a-b)/2] = (a-b)/2となるので、
{X(4a+1) - X(4b+1) - X(4(a-b))} mod 2 = {X(a) - X(b) - X(a-b) + (a-b)/2 - (a-b)/2 } mod 2 = {X(a) - X(b) - X(a-b)} mod 2
となります。

{X(a) - X(b) - X(a-b)} mod 2 = {X(a) + X(b) + X(a-b)} mod 2 であるので、{X(4a+1) + X(4b+1) + X(4(a-b))} mod 2 = {X(a) - X(b) - X(a-b)} mod 2 となり、K と L を 4 で割った余りは等しいので、A と B も 4で割った余りが等しいことが証明されました。