【東京大学2020年度前期入試数学(理系)第2問】心の余裕が試される問題

東大(理系)の2020年度入試数学第2問は平面図形の問題です。

通常、入試の問題では例を作って試すということをよく行いますが、この問題は特にそれが重要で、実際に図を書いて確かめていくと何を問われているかが分かります。

解答時間＝記述にかかる時間はともかく、難易度としては6問を通して最も易しいと思います。

第1問も易しいですが、第1問が一部の受験生を落とす効果がある一方、この問題は(通常の精神状態であれば)多くの受験生が取れると思います。

東京大学安田講堂
2016年12月24日、 Kakidai撮影、Wikipediaより

[問題] 平面上の点 P, Q, R が同一直線上にないとき，それらを 3 頂点とする三角形の面積を△PQR で表す。また，P, Q, R が同一直線上にあるときは，△PQR = 0 とする。
　A, B, C を平面上の 3 点とし，△ABC = 1 とする。この平面上の点 X が
　　　　　　　2 ≦ △ABX + △BCX + △CAX ≦ 3
を満たしながら動くとき，X の動きうる範囲の面積を求めよ。

この問題の最初の感触は？？？ですが、まずは図を描いてみようとなると思います。そして、描いていくうちに状況がつかめてきます。

どの問題でも「具体例で試す」というのは重要です。基本。

ですが、第1問で全く手を出せない受験生は、ここで余裕をなくしている可能性があります。そうなると最悪で、何をしていいかが分からずにさらなる泥沼に落ちる可能性がある。

東大の意図が手に取るようにわかります。(勝手な妄想)

でもおそらく、最初の2問を速攻で解いた受験生と、最初の2問で時間ばかり経過した受験生、両方いたはずです。どちらも一定の割合で。

それが東大の意図で、最初の2問で精神的に揺さぶりを入れて受験生を落としにかかったと見て間違いないでしょう。

もう一つ重要なポイントは、第1問も第2問も初見で「難しくない」と判断しそうなところです。

実際に易しいので正しい判断ですが、実は一番やりやすいのは第3問です。にもかかわらず、頭から解いていってハマる可能性がある。それが東大側の戦略と見ました。

(ちなみに、第3問は問題を解ききることはできますが、大きく減点される要素があります。)

さて解答に移ります。

場合分けは6つと言えば6つですが、実際には2つです。次の図を見てください。

辺AB, BC, CA を伸ばして直線することで三角形 ABC の外側を6つの領域(Region) に分けます。ただし、図の対称性から本質的には Region 1, 3, 5 と Region 2, 4, 6 の2種類に分かれます。

ただしその前に、点 X が 三角形 ABC 内にあるときを言及する必要があって、このときには △ABX + △BCX + △CAX = △ABC = 1 となります。

したがって、条件を満たす X は三角形 ABC の外側にあることになります。

ではまず点 X が Region 1 にある場合から。次の図を見てください。

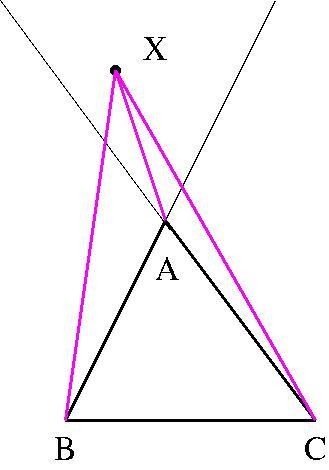
直線AB, AC に対して点 X が 三角形 ABC と反対側にあるため、△BCX = △ABX + △CAX + △ABC となります。

したがって、△ABX + △BCX + △CAX = △BCX × 2 - △ABC となるため、2 ≦  △BCX × 2 - △ABC ≦ 3 から 3/2 ≦ △BCX ≦ 2 が得られます。

辺BC を底辺と見なすと、三角形 BCX の高さは三角形 ABC の高さの 3/2 倍から 2 倍になっている必要があるので、点 X の領域は次の四角形DEGF となります。

ここで、AD = AB = 2 AF かつ AE = AC = 2 AG です。要するに三角形ABC ≡ 三角形 ADE で、なおかつ 三角形AFG は三角形ABCと相似比 1/2 の相似三角形になります。

以上のことから、四角形DEGF = 1 - (1/2)^2 = 3/4 となります。X が Region 3, 5 にあるときも同様です。

次に点 X が Region 2 にある場合を考えます。この場合は次のような図になります。

直線BC, CA に対して点 X が三角形ABC と同じ側にあるため、△BCX + △CAX = △ABX + △ABC となります。

したがって、△ABX + △BCX + △CAX = △ABX × 2 + △ABC となるため、2 ≦ △ABX × 2 + △ABC ≦ 3 から 1/2 ≦ △ABX ≦ 1 が得られます。

辺AB を底辺と見なすと、三角形ABX の高さは三角形 ABC の高さの 1/2 倍から 1 倍になっている必要があるので、点 X の領域は次の四角形HIKJ となります。

ここで、AK = AC = 2 IK かつ BJ = BC = 2 HJ です。要するに、三角形 CKJ と CIH は三角形 CAB とそれぞれ相似比が 2 と 3/2 の相似三角形になります。

以上のことから、四角形HIKJ = 2^2 - (3/2)^2 = 7/4 となります。点 X が Region 4, 6 にあるときも同様です。

よって、点 X の動きうる範囲の面積は (3/4 + 7/4) × 3 = 15/2 となります。

受験には落としてはいけない問題と落としてもいい(もっと言うと落とすべき)問題がありますが、この第2問は合格に向けて絶対に落とせない問題だと思います。ここで落としたら致命傷になります。

東大受験生の場合、この問題ができないとしたら精神的な理由の方が大きいと思います。

冗談抜きで心を鍛えることも受験では必要なので、どうすればいいかをアドバイスはできないですが、不動心を身につけて受験に挑んでください。