仮説検定における後決めの危険性～前編～

2023年11月30日 22:47

こんにちは、ゆるです。前回の投稿からかなり時期が空いてしまい申し訳ありません。今回は仮説検定の正しい使い方について触れていきたいと思います。
本記事を作成する上で、仮説検定の概念については以下の2冊の書籍を参考にしました。

また本記事では乱数を用いたシミュレーションを行いますが、その際には以下の書籍を参考にしました（本記事で扱うpythonと違い、Rをベースにした書籍である点ご注意ください）。

導入

生物学では論文内にあるデータの確からしさを担保するために仮説検定がよく用いられます。典型的な例としては以下のようなシチュエーションが挙げられます。

とあるがん細胞において薬剤Aを投与した群と投与していない群で増殖速度が変わるか
臨床試験において医薬品Bは疾患Cに罹患する患者の生存期間を延伸させる効果があるか

こういった仮説検定は生物、医療分野のみならず様々な場所で意思決定に関わっているのではないでしょうか。
この仮説検定は一般的なガイドラインとして、データ取得前にサンプルサイズや検定法を決定し、データ取得後仮説検定により有意な差があるかを判断します。この過程で、データ取得後に有意にならない場合にデータを追加して仮説検定をし直すことはp-hackingと呼ばれ、禁忌とされています。これがしっかりと守れている研究者がどれだけいるかは常に問題視され、様々な場所で議論されていると思います。
一方で、このp-hackingがなぜいけないのか、どれだけ危険なことなのかについて具体的なイメージを持っている研究者は多くないのではないでしょうか？本記事ではその点について具体例を交えて解説させて頂きたいと思います。またp-hackingはサンプルサイズの後決め以外にも、複数の仮説検定を試し有意になったものを採用する操作やデータの取得後選別も含め、より広義な不正も含む場合もありますが、今回はサンプルサイズの後決めに限った具体例を提示します（本質的にはなぜいけないかは共通だと考えています）。

帰無仮説下でp値が従う分布

生物学分野の研究者は、仮説検定の際にExcelやPrismなどで備え付けの関数を使って$${p}$$値を算出し、有意か否かを判断するだけの場合が多く、「$${p}$$値が従う分布」と言われてもピンとこない方が多いのではないでしょうか。一方で仮説検定を正しく使用する上で「帰無仮説下で$${p}$$値が従う分布」というのは理解するべき概念です。そこでまず、以下の事項を確認しましょう。

$${p}$$値とは、「帰無仮説下で統計検定量が従う分布において、実際にデータから算出された検定統計量の実現値以上（場合によっては「以下」）の値をとる確率」である。

【定義１】

ここで重要なことは、データが母集団分布から得られた確率変数であるとすると、そこから計算される$${p}$$値も確率変数になるということです。そしてこの$${p}$$値は、以下の性質が成り立ちます。

検定統計量が連続となる仮説検定において、帰無仮説が正しい場合、$${p}$$値は連続一様分布$${\mathcal{U}(0, 1)}$$に従う。

【性質１】

但し、「検定統計量が連続となる検定において」という断りがあるように、Fisherの正確確率検定などで離散分布の検定統計量を近似を用いずに$${p}$$値計算する場合は上記の限りではないので注意してください。
この$${p}$$値が従う分布は、バイオインフォマティクスの論文などでは出てくることがあるので、知っている方は知識として持っていたかもしれません。

一例を挙げてみます。トランスクリプトーム解析などで、同じサンプルを$${10}$$回micro arrayで測定を行うことを考えます。Micro arrayに馴染みのない方に少し説明させていただくと、mRNAに相補的な配列を持ったプローブによりmRNA量を網羅的に定量する測定系になります。例えば今回、$${5000}$$遺伝子に関してのmRNAを定量できたとします。その$${10}$$回分の測定をランダムに$${2}$$群に分割します（$${2,4,5,7,10}$$回目の測定を群A、残りを群Bといった感じです）。この$${2}$$群について、各遺伝子ごとに「$${2}$$群の平均が等しいという帰無仮説」に基づいて独立に検定を行った場合どういった結果が得られるでしょうか？全く同じサンプルから得られ、群分けもランダムに行っているので各遺伝子の検定において、帰無仮説「$${2}$$群の平均は等しい」は実際に正しいことになります。ここで、帰無仮説が正しい場合、$${p}$$値は$${\mathcal{U}(0, 1)}$$に従いかつ各遺伝子ごとの検定は独立に行われるので遺伝子ごとに得られた$${p}$$値のヒストグラムを描くと、$${0}$$から$${1}$$までほぼ同頻度で得られるという結果になるはずです。ここで逆に考えてみましょう。$${p}$$値が$${\mathcal{U}(0, 1)}$$に従うということは$${p < 0.05}$$を有意とした場合、$${5000}$$遺伝子のうち$${250}$$程度の遺伝子は差がないにもかかわらず有意になることです。これがまさに仮説検定における第一種の過誤というものの概念になります。

第一種の過誤とは帰無仮説が正しいにもかかわらず、帰無仮説を棄却してしまうことであり、その確率を慣例的に$${\alpha}$$と表す。

【定義２】

余談ですが、第二種の過誤は「対立仮説が正しいにもかかわらず帰無仮説を受容してしまうこと」であり、その確率を慣例的に$${\beta}$$で表します。さらに$${1-\beta}$$は検定の検出力と呼ばれるものであり、聞いたことある方も多いのではないでしょうか。この検出力はサンプルサイズ決定において非常に重要な概念ですがそれは今後別記事で触れようと思います。

少し概念的な話が続いたので帰無仮説下で$${p}$$値が従う分布について実際にシミュレーションしてみましょう。$${2}$$群の平均が等しいか否かについて$${t}$$検定を行う際には帰無仮説は「$${2}$$群の平均が等しい」となります。そのため今回はその帰無仮説の状況を模して、標準正規分布からサンプルサイズ$${6}$$の標本を$${2}$$群分取得し、$${t}$$検定を行います。何度もくどいかもしれませんが今回の$${2}$$群は同一の分布から得られた標本なため、実際の平均は等しく、検定の結果は有意（$${p < 0.05}$$）になってほしくありません。$${p}$$値が従う分布を可視化するため$${1}$$万回シミュレーションしてみます。以下のコードでシミュレーションが可能です。

"""
以下の１～３を1万回シミュレーションし、最後にp値のヒストグラムを描画する
１．標準正規分布から独立同一に得られたN=6の2つの標本群をＸ，Ｙとする。
２．群Ｘ，Ｙの平均についてStudentのt検定（両側検定）を行う。
３．ｐ値をリストに格納
"""

#モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sts

#p値を格納するリスト
pval_list = []

#１万回シミュレーション
for i in range(10000):
    X = np.random.normal(loc=0, scale=1, size=6)
    Y = np.random.normal(loc=0, scale=1, size=6)
    pval =  sts.ttest_ind(X, Y, equal_var=True, alternative='two-sided').pvalue
    pval_list.append(pval)

#ヒストグラム描画
plt.hist(pval_list, bins=20)
plt.show()

このコードを実行すると「$${2}$$群の標本抽出と$${t}$$検定」を$${1}$$万回行った際の$${p}$$値のヒストグラムを表示します。ゆるが実行した際は以下のようになりました。$${p<0.05}$$の割合が分かりやすいようにヒストグラムは$${0.05}$$刻みに設定してあります。

以上より、帰無仮説下における状況、つまり$${2}$$群の平均の検定においてそれらの平均が等しい場合には検定の結果である$${p}$$値が$${0}$$から$${1}$$の範囲の連続一様分布$${\mathcal{U}(0, 1)}$$に従うことが実際にイメージついたかと思います。これにより$${p<0.05}$$となる確率が$${0.05}$$となり、第一種の過誤の確率が$${0.05}$$に抑えられる訳です。

ではようやく本題に入りますが、サンプルサイズを予め決めず、検定の結果に応じてサンプルサイズを変化させるといった戦略をとった場合どうなるか次章で検証したいと思います。

サンプルサイズを後決めした際のp値の分布

本来、実験を行う際のサンプルサイズ決定は$${n=3}$$など予め決めてから実験を実施し、全てのデータをとり終わってから仮説検定によって$${p}$$値を算出し有意差があるかを判定します。
しかし、ここでもし$${n=3}$$で検定を行い、有意になれば有意差があると結論付け、有意にならなかった場合もう$${1,2}$$回実験して再度仮説検定を行うという戦略をとった場合どうなるでしょうか？これは決まりとしてダメだとわかっている方が多いと思いますが、何がだめなのか説明できるでしょうか？結論から言うと、「$${p}$$値の分布が変化することで、有意水準$${0.05}$$で検定しているにもかかわらず第一種の過誤率が$${0.05}$$より大きくなってしまう」からです。そしてこのようなサンプルサイズ付け足し手法を用いると、究極的には本来平均の差がないデータであっても高確率で有意にさせてしまうことができてしまいます。そのため帰無仮説下での$${p}$$値の分布が適切になるように実験計画を設計し、第一種の過誤、第二種の過誤を適切にコントロールしなければなりません。理論的な話ばかりではイメージしづらいかと思うので、以下の事例でシミュレーションしてみましょう。

標準正規分布から$${n=3}$$の標本を$${2}$$群分取得する。$${Student}$$の$${t}$$検定を行い、有意差が出ればその検定の$${p}$$値を最終的な$${p}$$値として報告する。有意差が出なければ各群もう$${1}$$サンプルずつ同じ分布から抽出し、再度$${t}$$検定を行う。ここで有意になればその検定の$${p}$$値を最終的な$${p}$$値として報告する。それでも有意にならない場合は再びサンプルサイズを$${1}$$つずつ増やして検定をかけ、ここでの検定の結果は有意になろうとなるまいとその検定の$${p}$$値を最終的な$${p}$$値として報告する。

【事例１】

少しわかりにくいかもしれませんが、$${n=3}$$から始めて有意差が出なければ$${n=5}$$まで粘り、それでも有意にならなければ諦めるといったシチュエーションになります。この状況は以下のコードで検証可能になります。

#モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sts

#p値を格納するリスト
pval_list = []

#１万回シミュレーション
for i in range(10000):
    #とりあえずn=3ずつサンプルを準備
    X = np.random.normal(loc=0, scale=1, size=3)
    Y = np.random.normal(loc=0, scale=1, size=3)
     #t検定     pval =  sts.ttest_ind(X, Y, equal_var=True, alternative='two-sided').pvalue
    if pval >= 0.05:
        #有意にならなかった場合、サンプルサイズを1ずつ増やして再度検定
        X = np.append(X, np.random.normal(loc=0, scale=1, size=1))
        Y = np.append(Y, np.random.normal(loc=0, scale=1, size=1))
        pval =  sts.ttest_ind(X, Y, equal_var=True, alternative='two-sided').pvalue
        if pval >= 0.05:
            #有意にならなかった場合、サンプルサイズを1ずつ増やして再度検定（但しこれ以上は有意にならなくても諦める）
            X = np.append(X, np.random.normal(loc=0, scale=1, size=1))
            Y = np.append(Y, np.random.normal(loc=0, scale=1, size=1))
            pval =  sts.ttest_ind(X, Y, equal_var=True, alternative='two-sided').pvalue
        else:
            pass
    else:
        pass
    pval_list.append(pval)

#ヒストグラム描画
plt.hist(pval_list, bins=20)
plt.show()

このコードで$${1}$$万回シミュレーションした後の$${p}$$値の分布は以下のようになります（この次に示すコードのように書くことでよりスマートにコーディング可能なのですが今回は上記の方が可読性が高いと判断して少し回りくどい書き方になっています）。

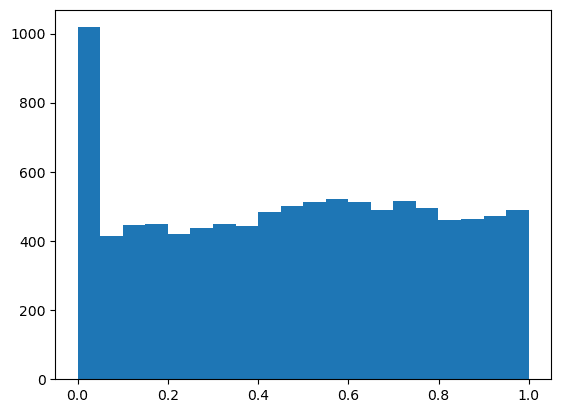
ヒストグラムからも分かるように、$${10}$$%程度の割合で$${p<0.05}$$となっています。これは全く同じ分布から抽出していて本来差がない（＝帰無仮説の状況）にもかかわらず$${0.1}$$程度の割合で帰無仮説を棄却してしまうことを示唆しており、第一種の過誤率が$${5}$$%の倍になってしまってることを指します。ここで大事なことは、「平均に差がないと仮定したときにこのデータが得られる確率は非常に低いので差があるだろう」という概念に基づく仮説検定は、第一種の過誤率を保てないとその概念がそもそも成り立たないということです。そのためこのようなサンプルサイズ後決めは御法度となります。

もしかしたらまだ「所詮第一種の過誤率が$${2}$$倍になる程度で、サンプル数がもっと増えれば平均値も安定してきて実際に差がないデータは有意にならないでしょ」と思われる方がいるかもしれないので、さらに過激な実験をしてみましょう。先ほどは$${n=5}$$まででしたが、それを$${n=1000}$$まで増やしてみました笑。以下のコードで実行可能です（先ほどよりもよりスマートなコーディングになっています）。

#モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sts
from tqdm import trange

#p値を格納するリスト
pval_list = []

#１万回シミュレーション
for i in trange(10000):
    X = np.random.normal(loc=0, scale=1, size=3)
    Y = np.random.normal(loc=0, scale=1, size=3)
    pval =  sts.ttest_ind(X, Y, equal_var=True, alternative='two-sided').pvalue
    n = 3
    while pval >= 0.05 and n<=1000:
        #有意になるかn=1000になるまで「サンプルサイズ+1と検定」を繰り返す
        X = np.append(X, np.random.normal(loc=0, scale=1, size=1))
        Y = np.append(Y, np.random.normal(loc=0, scale=1, size=1))
        n += 1
        pval =  sts.ttest_ind(X, Y, equal_var=True, alternative='two-sided').pvalue
    pval_list.append(pval)

#ヒストグラム描画
plt.hist(pval_list, bins=20)
plt.show()

実際に実行すると数十分かかるのでtqdmで進度をモニターした方が不安にならずに済みます笑。得られた$${p}$$値のヒストグラムは以下のようになります。

なんと、実際には差がないのに$${50}$$%の割合で有意差を錬成することが可能になりますね笑。第一種の過誤率が$${0.05}$$になるようにとの意図の$${p<0.05}$$という閾値なのに、その過誤率が$${0.5}$$になるという恐ろしい結果です。この例はさすがに極端ですが、有意差は不正に錬成できてしまうという危機感を持っていただけたならこの実験の意味があったと思います。

前編まとめ

以上が仮説検定における後決めの危険性の実例になります。仮説検定は原理を理解しようとする姿勢が大事というスタンスになられた方が少しでも多くなれば幸いです。前編は以上になりますが、後編ではなぜ$${p}$$値が帰無仮説下で連続一様分布に従うのかについて、より統計数理の観点から考察する予定です。ここまで読んで下さった方々、ありがとうございました。それではまた次回！

(2023/12/17 追記) 後編を公開しました！

【更新履歴】
2023/11/30 初稿投稿
2023/12/17 後編へのリンク追加

この記事が気に入ったらサポートをしてみませんか？