
仮説検定における後決めの危険性~後編~
こんにちは、ゆるです。前回は仮説検定におけるサンプルサイズ後決めの危険性について扱い、帰無仮説下において$${p}$$値が$${\mathcal{U}(0, 1)}$$に従うこと、そしてp-hackingにおいてはその分布が変化することで検定の第一種の過誤率が変化することを述べました。
後編ではそもそもなぜ帰無仮説下で$${p}$$値が$${\mathcal{U}(0, 1)}$$に従うかについて扱いたいと思います。今回の記事は実務上は意識する必要のないことではありますが、数理統計学に興味が出てきた方にはさらにのめりこむきっかけとして読んで頂けると嬉しいです!
本記事を執筆する上で、以下の書籍を参考にしました。
累積分布関数による変数変換
帰無仮説下で$${p}$$値が従う分布を考える上で必要な事項として、「累積分布関数による確率変数の変数変換」が挙げられます。少し統計数理の色が強くわかりづらいかと思いますので嚙み砕いて説明します。
$${X}$$を連続型の確率変数とし、その確率密度関数を$${f(x)}$$、累積分布関数を$${F(x)}$$とします。累積分布関数は確率変数$${X}$$が$${x}$$以下の値をとる確率を表すため
$$
{F(x) =\int_{-\infty}^{x}f(t)dt}
$$
となります。ここで、$${X}$$が確率変数であることから、$${F(X)}$$は$${X}$$を変数変換した確率変数と考えることができます(小文字の$${x}$$は$${X}$$の実現値で、大文字の$${X}$$は確率変数である点注意してください)。ここで$${F(X)}$$が従う分布が何かについて考えたいと思います。
ここで具体例を出してイメージしやすくしましょう。確率密度関数、累積分布関数が単純な形式で書けるということで指数分布について扱いたいと思います。指数分布は単一のパラメータ$${\lambda}$$を持つ分布であり、密度関数は以下のように表せます。
$$
{f(x;\lambda)=\lambda e^{-\lambda x} \quad (x\ge 0)}
$$
また、累積分布関数は以下のように表せます。
$$
{\begin{split} F(x;\lambda) &=\int_{0}^{x}f(t;\lambda)dt\\
&=\int_{0}^{x}\lambda e^{-\lambda t}dt\\
&=\left[-e^{-\lambda t}\right]_{0}^{x}\\
&=1-e^{-\lambda x}
\end{split}}
$$
今考えているのは確率変数$${X}$$が指数分布に従う時、$${F(X)=1-e^{-\lambda X}}$$がどのような分布に従うかということです。$${\lambda=1}$$の場合で実際にシミュレーションしてみましょう。以下のコードで実行可能です。
"""
以下の1~2を1万回シミュレーションし、Yのヒストグラムを描画することで、Yの従う分布を確認する。
1.lambda=1の指数分布から確率変数Xを取得する。
2.Y = 1-exp(-X)とする。
"""
#モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
#指数分布から1万サンプル抽出してヒストグラム表示
X = np.random.exponential(scale=1, size=10000)
plt.hist(X, bins=20)
plt.show()
#XをYに変数変換してからYのヒストグラムを表示
Y = 1-np.exp(-X)
plt.hist(Y, bins=20)
plt.show()一つめのプロットでは指数分布から適切に抽出できているかの確認で、以下のように表示されると思います。
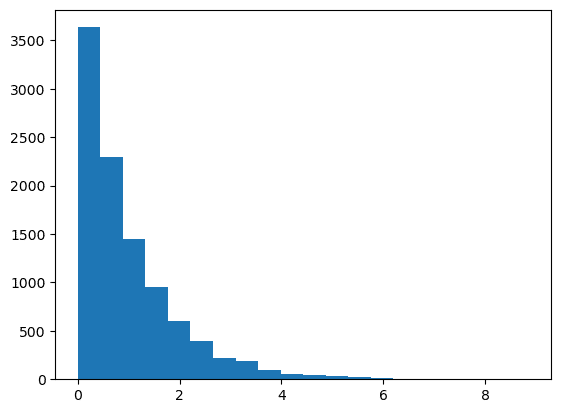
二つ目のプロットが$${Y=F(X)=1-e^{-X}}$$のヒストグラムになります。

シミュレーションの結果、$${Y=F(X)}$$は$${\mathcal{U}(0, 1)}$$に従うことが示唆されました!今回、指数分布に限ったシミュレーションを行いましたが、実はこの性質は分布によらず成り立ちます。以下が一般的な性質になります。
連続確率変数$${X}$$の累積分布関数$${F_X(x)}$$が狭義単調増加であるとき、$${Y=F_X(X)}$$は$${\mathcal{U}(0, 1)}$$に従う。
この定理を証明するために、また別の以下の定理が必要になります。
連続確率変数$${U}$$の累積分布関数を$${F_U(u)}$$としたとき、$${F_U(u)=u}$$であれば$${U~\mathcal{U}(0, 1)}$$となる。
$${[0,1]}$$の範囲の連続一様分布の確率密度関数が$${f_U(u)=1}$$であり累積分布関数が$${F_U(u)=u}$$であること、そして分布と累積分布関数が一対一対応であることから、【定理2】はイメージしやすいかと思います。以上より、【定理1】を証明しようと思ったら、$${Y=F_X(X)}$$の累積分布関数が$${F_Y(y)=y}$$となることを証明すればよい訳です。
$$
{\begin{split} F_Y(y) &=P(Y\le y)\\
&=P(F_X(X)\le y)\\
&=P(X\le F_X^{-1}(y))\\
&=F_X(F_X^{-1}(y))\\
&=y
\end{split}}
$$
以上より、$${Y=F_X(X)}$$の累積分布関数が$${F_Y(y)=y}$$となることから、$${Y}$$は$${\mathcal{U}(0, 1)}$$に従うことが示されました。
p値が帰無仮説下で0から1の連続一様分布に従う理由
さて本題に戻ります。本記事では$${p}$$値が$${\mathcal{U}(0, 1)}$$に従う理由について考えているのでした。ここで$${p}$$値とはなんだったか確認しましょう。
$${p}$$値とは、「帰無仮説下で統計検定量が従う分布において、実際にデータから算出された検定統計量の実現値以上(場合によっては「以下」)の値をとる確率」である。
上記の定義は厳密には片側検定の場合についての話になります。今回は簡便のため片側検定の範囲で議論を行いたいと思います(両側検定の場合も$${p}$$値が$${\mathcal{U}(0, 1)}$$に従う理由は本質的に同じなのですが、例えば$${t}$$検定などでは$${p}$$値が上記の定義の倍になるなど、変数変換が加わります)。
今、ある片側の仮説検定において検定統計量を$${T}$$、その実現値を$${T=t}$$とします。$${T}$$が帰無仮説下で従う分布の累積分布関数を$${F_T(t)}$$とします。【定義1】において、「実際にデータから算出された検定統計量の実現値『以上』の値をとる確率」としたとき、$${p}$$値は$${1-F_T(t)}$$に相当します。これは特定の実現値の場合の$${p}$$値となりますが、「$${p}$$値が従う分布」を考える際には確率変数$${T}$$の変数変換として$${1-F_T(T)}$$の従う分布が$${p}$$値の従う分布となります。【定理1】より$${F_T(T)}$$は$${\mathcal{U}(0, 1)}$$に従うので、$${1-F_T(T)}$$も$${\mathcal{U}(0, 1)}$$に従います。以上より、$${p}$$値が帰無仮説下において、$${[0,1]}$$の範囲の連続一様分布に従うことが示されました。
まとめ
前編後編と通して、「$${p}$$値が従う分布」という切り口から仮説検定において従わなければならないルールについて議論しました。特に後編では数理の色が濃く、分かりにくい説明があったかもしれませんが、前編でのシミュレーションから仮説検定の原理を理解しようとする姿勢が、意識外の研究不正の防止につながるというマインドが芽生えて頂けたのなら本記事を書き、読んで頂いたことに意味があったと思えます。読んで下さった方々、ありがとうございました。
次記事ではパラメトリックvsノンパラメトリックといったようにどの検定がどういった性質を持っているのかについて、今回の記事をふまえてご紹介する予定です。是非次回も読んで頂けると嬉しいです!それではまた!
【更新履歴】
2023/12/17 初稿投稿
この記事が気に入ったらサポートをしてみませんか?
