ｔ検定を掘り下げる～中編～

こんにちは、ゆるです。前回ｔ検定に関する記事を書きましたが、「ｔ分布出てこないじゃないか！」という感想で終わってしまった方も多いかもしれません。本記事では１群の平均値の検定（分散未知）について扱い、いよいよｔ分布が出てきます。
もしまだ前編を読まれていない場合は、前編から読んでいただいた方が理解が深まると思います！

本記事を作成する上でｔ検定やｔ分布の枠組みに関しては以下の2つの書籍を参考にしました。

増訂版　日本統計学会公式認定　統計検定１級対応　統計学

現代数理統計学の基礎 (共立講座 数学の魅力 11)

また、本記事では乱数を使用したシミュレーションを扱いますが、モンテカルロシミュレーションの枠組みについては以下の書籍を参考にしました（言語が本記事のpythonと違い、Ｒである点注意してください）。

Rによるモンテカルロ法入門

前編のおさらい

ｔ検定におけるｔとはｔ分布のｔであることに触れ、ｔ分布の導入として数理統計学の教科書では

標準正規分布に従う確率変数$${Z}$$と自由度$${p}$$の$${\chi^2}$$分布に従う確率変数$${W}$$があり、それら二つが独立であるとき、$${Z/\sqrt{W/p}}$$は自由度$${p}$$の$${t}$$分布に従う

という説明がされることを述べました。さらに、ｔ検定を学ぶ前段階として「１群の平均の検定（分散既知）」について扱い、

母集団分布が分散$${\sigma^2}$$と分かっている正規分布に従っているが、その平均が分からないとする。この時、その分布から得られた標本$${X_1, X_2, …, X_n }$$を用いて、母集団分布の平均が$${\mu}$$に等しいかを検定せよ。

という形式の検定において、検定統計量を

$$
{T(X_1, X_2, …, X_n) = (\overline{X}-\mu)/{\sqrt{\sigma^2/n}}}
$$

とし、$${T(X_1, X_2, …, X_n)}$$が帰無仮説$${H_0}$$下で標準正規分布$${\mathcal{N}(0, 1)}$$に従うことから$${p}$$値を算出できました。また、$${\mathcal{N}(0, 1)}$$はZ分布と呼ばれることから、検定統計量がZ分布に従う本検定はZ検定とも呼べると述べました。
本記事では同じく１群の平均値の検定ですが、分散が未知の場合について考えていきましょう。

１群の平均値の検定（分散未知）

１群の平均値の検定（分散既知）と同様、まず問題設定をしてみましょう。以下のような問いを考えてみてください。

母集団分布が正規分布に従っているとするとき、その分布から得られた標本$${X_1, X_2,…  X_n}$$を用いて母集団分布の平均が$${\mu}$$に等しいか検定せよ。

【問題１】

今回もより具体的なシチュエーションとして、

A国の男性の身長は正規分布に従っていると仮定する。いま、A国の男性を$${6}$$人連れてきたところ、身長が$${182, 177, 171, 175, 180, 183\text{ cm}}$$であった。このとき、A国の男性の平均身長が$${173\text{ cm}}$$か否か検定せよ。

【問題２】

という問題を例に挙げてみます。分散既知の場合と比べて問題自体はよりシンプルかつ現実的ではないでしょうか笑。Z検定で使用した検定統計量

$$
{T(X_1, X_2, …, X_n) = \frac{\overline{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}}}
$$

には$${\sigma^2}$$という既知の値が含まれますが、これが分散未知の場合には変える必要があります。おそらく

$$
{T(X_1, X_2, …, X_n) = \frac{\overline{X}-\mu}{\sqrt{\frac{?}{n}}}}
$$

という何となくのイメージを持たれる方が多いのではないでしょうか。この「？」は未知の分散を推定した値$${\tilde{\sigma^2}}$$になります。そこで、分散の推定値について考えてみましょう。母集団分布の分散の推定値には複数種類あり、最尤推定量

$$
{\tilde{\sigma^2}^{ML} = \frac{1}{n}\sum_{i=1}^n{(X_i-\overline{X})^2}}
$$

もしくは不偏推定量

$$
{\tilde{\sigma^2}^{U} = \frac{1}{n-1}\sum_{i=1}^n{(X_i-\overline{X})^2}}
$$

が知られています。最尤推定量の$${ML}$$は「最尤」を意味する"maximum likelihood"の略として、不偏推定量の$${U}$$は「不偏」を意味する"unbiased"の略として慣例的につけました。ここで、これらの分散の推定量を先ほどの検定統計量の式

$$
{T(X_1, X_2, …, X_n) = \frac{\overline{X}-\mu}{\sqrt{\frac{\tilde{\sigma^2}}{n}}}}
$$

の$${\tilde{\sigma^2}}$$に代入したとき、それぞれ

$$
{T_{ML}(X_1, X_2, …, X_n) = \frac{\overline{X}-\mu}{\sqrt{\frac{\tilde{\sigma^2}^{ML}}{n}}}}
$$

または

$$
{T_{U}(X_1, X_2, …, X_n) = \frac{\overline{X}-\mu}{\sqrt{\frac{\tilde{\sigma^2}^{U}}{n}}}}
$$

となります。前編で仮説検定の構成法について触れましたが、それに習うと、これらの検定統計量が帰無仮説$${H_0}$$下で従う分布を考えればよさそうです。一方で$${T_{ML}(X_1, X_2, …, X_n)}$$や$${T_{U}(X_1, X_2, …, X_n)}$$の分布の導出は一筋縄ではいかなそうです。そこで注目して頂きたい性質が以下になります。

確率変数$${X_1, X_2,…, X_n}$$が独立に正規分布$${\mathcal{N}(\mu, \sigma^2)}$$に従うとき、$${Z = \frac{\overline{X} - \mu}{{\sqrt{\frac{\sigma^2}{n}}}}}$$は$${\mathcal{N}(0, 1)}$$
に従う。また不偏分散$${V = \frac{1}{n-1}\sum_{i=1}^n{(X_i-\overline{X})^2}}$$について、$${W = (n-1)V/\sigma^2}$$は自由度$${n-1}$$の$${\chi^2}$$分布に従う。さらにこのとき、$${Z}$$と$${W}$$は独立となる。

自由度$${n-1}$$の$${\chi^2}$$分布とは？となる方が多いかもしれませんが、この$${\chi^2}$$分布についても説明をするのは本筋から外れすぎるかと思うので、今後の記事で扱いたいと思います。ただ生物統計学などで、

といった2x2の分割表（この表の数字は適当であり、何かしらの研究事実に基づくものではありません）を見かけた際に喫煙と肺がんの関連を調べる目的で$${\chi^2}$$検定をかけたことがある方も多いのではないでしょうか？この$${\chi^2}$$検定の$${\chi^2}$$は$${\chi^2}$$分布の$${\chi^2}$$なので、実は皆さんにも馴染み深い分布の一つかもしれません。
さて話を戻しますが、

$$
{Z = \frac{\overline{X} - \mu}{{\sqrt{\frac{\sigma^2}{n}}}}}
$$

が$${\mathcal{N}(0, 1)}$$に従うことについては前編で扱ったのでそちらをご参照ください。一方で不偏分散$${V}$$について、

$$
{W = \frac{(n-1)V}{\sigma^2}}
$$

が自由度$${n-1}$$の$${\chi^2}$$分布に従うのはイメージしにくいかと思われます。そこで【問題２】を例にとり、pythonを使ったシミュレーションにより確認してみましょう。今回、帰無仮説$${H_0}$$下における$${W}$$の分布を考えるので、母集団分布は$${\mathcal{N}(173, 25)}$$に従い、そこから$${n=6}$$の標本を抽出する場合を考えます。以下のコードで$${W}$$が自由度$${n-1=5}$$の$${\chi^2}$$分布に従うかを確認することができます。今回、【問題２】においては母集団分布の分散は未知ですが、$${W}$$を計算する過程で分散の値が必要であるため、便宜上$${\sigma^2=25}$$として計算します。

#モジュールのインポート
import numpy as np
import scipy.stats as sts
import matplotlib.pyplot as plt
import math

#10万回シミュレーションする
mu = 173 #平均
sigma2 = 25 #分散
n = 6 #標本数
W_list = [] #Wを格納するリスト
for i in range(100000):
X_list = np.random.normal(loc=mu, scale= math.sqrt(sigma2), size=n) #正規分布から6つの標本を得る
X_mean = X_list.mean() #平均
V = ((X_list-X_mean)**2).sum()/(n-1) #不偏分散V
W_list.append((n-1)*V/sigma2) #VをWに変換しリストに格納

#可視化
pdf_x = np.linspace(0, 25, 10000) #密度関数を描画するためのx座標
plt.hist(W_list, bins=50, density=True) #上記シミュレーションのヒストグラム
plt.plot(pdf_x, sts.chi2.pdf(pdf_x, df=n-1)) #自由度n-1のX^2分布の密度関数表示
plt.xlim(0, 25)
plt.show()

実行すると以下のような図が生成されるのではないでしょうか。

これはシミュレーションにより生成した$${W}$$のヒストグラム（青）と自由度$${5}$$の$${\chi^2}$$分布の密度関数（オレンジ）になります。「密度関数」という言葉を聞きなれない方もいるかもしれませんが、密度関数とは「連続分布において、確率変数$${X}$$の特定の範囲の値をとりうる確率」を与えるための関数です。上記のオレンジの線を表す関数を$${f(x)}$$とすると、$${X}$$が$${a}$$から$${b}$$の範囲の値をとる確率は

$$
{\int_{a}^{b}{f(x) dx}}
$$

となります。そして実際に得られたデータについて、ヒストグラムを全体の比率として表示した場合、密度関数と同様の形となります。
以上より不偏分散$${V}$$について、$${W = (n-1)V/\sigma^2}$$が自由度$${n-1}$$の$${\chi^2}$$分布に従うというイメージがついたと思います。
次に先ほどの$${Z}$$と$${W}$$についてはそれぞれが従う分布に加えてもう一つ重要な性質がありました。それは、$${Z}$$と$${W}$$が独立であるということです。こちらに関してはほとんどの方が疑問に思われると思います。おそらくそれは、$${Z = \frac{\overline{X} - \mu}{{\sqrt{\sigma^2/n}}}}$$にも$${W = \frac{(n-1)V}{\sigma^2}}$$内の$${V = \frac{1}{n-1}\sum_{i=1}^n{(X_i-\overline{X})^2}}$$にも$${\overline{X}}$$が含まれることからくる感覚なのではないでしょうか。その感覚については非常に強く同意できるところではあります。しかしその直観とは裏腹に、標本$${X_1, X_2,…, X_n}$$を抽出した母集団が正規分布に従うのであれば、これら$${Z}$$と$${W}$$は独立となります。この独立性の証明は、ゆるふわnoteの範囲を大きく逸脱すると判断し、記事冒頭に挙げた参考図書に委ねたいと思います。一方でシミュレーションによりこの独立性を可視化することはできます。一般に確率変数$${X}$$と$${Y}$$が独立であるとき、それらは無相関（相関係数$${\rho=0}$$）であることが知られています。但し$${X}$$と$${Y}$$について$${\rho=0}$$だからといってそれら二つの確率変数が独立とは限らないことには注意が必要です。今回、シミュレーションするのは$${Z}$$と$${W}$$の相関についてなので、あくまで証明というわけではなく独立っぽさの雰囲気を表すものになります。以下のコードで$${Z}$$と$${W}$$の相関係数をシミュレーションできます。また、先ほど同様、【問題２】においては母集団分布の分散は未知ですが、$${Z}$$と$${W}$$を各々計算する過程で分散の値が必要であるため、便宜上$${\sigma^2=25}$$として計算します。

#モジュールのインポート
import numpy as np
import scipy.stats as sts
import matplotlib.pyplot as plt
import math
#帰無仮説下での正規分布のパラメータ
mu = 173 #平均
sigma2 = 25 #分散
n = 6 #標本数
Z_list = [] #Zを格納するリスト
W_list = [] #Wを格納するリスト
#1万回シミュレーションする
for i in range(10000):
    X_list = np.random.normal(loc=mu, scale= math.sqrt(sigma2), size=n) #正規分布から6つの標本を得る
    X_mean = X_list.mean() #平均
    Z = (X_mean-mu)/math.sqrt(sigma2/n) #Zの計算
    V = ((X_list-X_mean)**2).sum()/(n-1)  #不偏分散     W = (n-1)*V/sigma2
    Z_list.append(Z)
    W_list.append(W)
rho = np.corrcoef(Z_list, W_list)[0,1] #相関係数
print(rho)

実行すると、おおよそ$${10^{-3}}$$オーダーあたりの数字が表示されるのではないでしょうか（今ゆるが実行したところ$${0.0038877…}$$となりました）。これはつまり、$${Z}$$と$${W}$$の相関係数が$${0}$$であると言って差し支えないかと思います。さらに、上記に続けて以下のコード

#平均と不偏分散の同時分布の散布図
plt.scatter(Z_list, W_list, s=1, c="black")
plt.xlabel("Z")
plt.ylabel("W")
plt.show()

を実行すると$${Z}$$と$${W}$$を平面上にプロットでき、

といったような図が描画されかと思われます。ぱっと見ても相関なさそうですよね！！以上より$${Z}$$と$${W}$$は独立ということまでは言えずとも$${\overline{X}}$$という共通構成要素を持ちながらも相関がなさそうだというイメージを持っていただけたかと思います。少し話が長くなりましたが、ここで改めてｔ分布に従う確率変数の構成法と、正規分布に従う標本が持つ性質を並べてみたいと思います。

標準正規分布に従う確率変数$${Z}$$と自由度$${p}$$の$${\chi^2}$$分布に従う確率変数$${W}$$があり、それら二つが独立であるとき、$${\frac {Z}{\sqrt{W/p}}}$$は自由度$${p}$$の$${t}$$分布に従う

確率変数$${X_1, X_2,…, X_n}$$が独立に正規分布$${\mathcal{N}(\mu, \sigma^2)}$$に従うとき、$${Z = \frac{\overline{X} - \mu}{{\sqrt{\frac{\sigma^2}{n}}}}}$$は$${\mathcal{N}(0, 1)}$$
に従う。また不偏分散$${V = \frac{1}{n-1}\sum_{i=1}^n{(X_i-\overline{X})^2}}$$について、$${W = \frac{(n-1)V}{\sigma^2}}$$は自由度$${n-1}$$の$${\chi^2}$$分布に従う。さらにこのとき、$${Z}$$と$${W}$$は独立となる。

見比べてみると次に何をするかが見えてくるかと思います。ｔ分布に従う確率変数の構成法においては標準正規分布$${\mathcal{N}(0, 1)}$$に従う確率変数に加えそれと独立に$${\chi^2}$$分布に従う確率変数が必要ですが、正規分布に従う標本から構成される確率変数$${Z}$$と$${W}$$はまさにこの要件を満たすのです！以上より次の式が導出されます。

確率変数$${X_1, X_2,…, X_n}$$が独立に正規分布$${\mathcal{N}(\mu, \sigma^2)}$$に従うとき、$${Z = \frac{\overline{X} - \mu}{{\sqrt{\frac{\sigma^2}{n}}}}}$$、$${V = \frac{1}{n-1}\sum_{i=1}^n{(X_i-\overline{X})^2}}$$、$${W = (n-1)V/\sigma^2}$$とすると、$${\frac{Z}{\sqrt{\frac{W}{(n-1)}}}}$$は自由度$${n-1}$$の$${t}$$分布に従う

ここで出てきた値をさらに整理すると以下のようになります。

$$
{\frac{Z}{\sqrt{\frac{W}{(n-1)}}} = \frac{\overline{X}-\mu}{\sqrt{\frac{V}{n}}}}
$$

これを検定統計量$${T(X_1, X_2, …, X_n)}$$とすることで、自由度$${n-1}$$のｔ分布に従う統計量として$${p}$$値が計算できるようになります。そしてこの形式の検定こそが「１群の平均値の検定（分散未知）」となります！さらに重要なこととして先ほどシミュレーションまでは分散未知と言いつつ便宜上分散の値を決めていましたが、整理した$${Z/\sqrt{W/(n-1)}}$$には母集団分布の真の分散$${\sigma^2}$$が含まれておらず分散の値が未知でもこの統計量を計算することが可能です！以上より、構成した$${T(X_1, X_2, …, X_n)}$$に得られたデータを実際に代入して得られた値を$${T}$$としたとき、自由度$${n-1}$$のｔ分布において、$${T}$$以上（or 以下）の値をとる確率の倍の値が$${p}$$値となります（この手順については前編をご参照ください）。
ｔ分布に従う検定統計量を構成するまで前編からかなり長い道のりを辿りましたね…。ここまでついて来てくださった方々ありがとうございます！ただここで終わりではなくさらに考察を続けようと思います。
この統計量$${T(X_1, X_2, …, X_n)}$$が従うｔ分布についても【問題２】の状況で分布の密度関数の概形を確認していきます。以下のコードで確認が可能です。

#モジュールのインポート
import numpy as np
import scipy.stats as sts
import matplotlib.pyplot as plt
import math
#帰無仮説下での正規分布のパラメータ
mu = 173 #平均
sigma2 = 25 #分散
n = 6 #標本数
T_list = [] #Tを格納するリスト
#10万回シミュレーションする
for i in range(100000):
X_list = np.random.normal(loc=mu, scale= math.sqrt(sigma2), size=n) #正規分布から6つの標本を得る
X_mean = X_list.mean() #平均
Z = (X_mean-mu)/math.sqrt(sigma2/n) #Zの計算
V = ((X_list-X_mean)**2).sum()/(n-1)  #不偏分散 W = (n-1)*V/sigma2
T = Z/math.sqrt(W/(n-1))
T_list.append(T)

#可視化
pdf_x = np.linspace(-10, 10, 10000) #密度関数を描画するためのx座標
plt.hist(T_list, bins=200, density=True) #上記シミュレーションのヒストグラム
plt.plot(pdf_x, sts.t.pdf(pdf_x, df=n-1), label="Chi square (df=5)") #自由度5のX^2分布の密度関数表示
plt.plot(pdf_x, sts.norm.pdf(pdf_x), label="Standard normal") #標準正規分布の密度関数表示
plt.plot(pdf_x, sts.cauchy.pdf(pdf_x), label="Cauchy") #コーシー分布の密度関数表示
plt.xlim(-10, 10)
plt.legend()
plt.show()

このコードを実行すると以下のような図が描画されると思います。

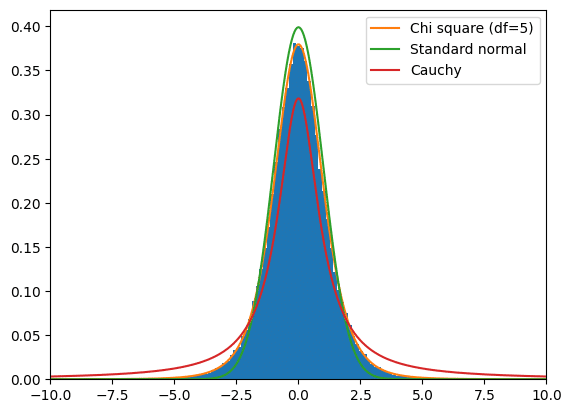
少々追加情報も入れたので追って説明させていただきます。帰無仮説$${H_0}$$下においては母集団分布から$${6}$$つの標本$${X_1, X_2,…, X_6}$$を抽出するとそれらは$${\mathcal{N}(173, 25)}$$に従います。そこから上記の要領で構成される検定統計量$${T(X_1, X_2, …, X_n)}$$をシミュレーションにより10万回生成してヒストグラムにしたのが青のグラフです。ここで$${T(X_1, X_2, …, X_n)}$$は自由度$${6-1=5}$$のｔ分布に従うと上記で述べましたが、実際にヒストグラムは自由度$${5}$$のｔ分布の密度関数（オレンジ）に高精度で一致します。ここで標準正規分布（緑）とコーシー分布（赤）の密度関数も表示してみましたがこれら二つは近しい形をしつつも青のヒストグラムとピッタシ一致するというわけではなさそうです。ｔ分布は自由度という概念があることからわかるように、密度関数内にも自由度を代入するパラメータが存在します（具体的な関数系を書くのは変数変換やベータ関数という少々発展的な内容を含むので今後の解説に回したいと思います）。このｔ分布について自由度に相当するパラメータに$${1}$$を代入するとコーシー分布と呼ばれる裾野が広い分布になり、逆に自由度のパラメータを$${+\infty}$$に飛ばすと関数形が標準正規分布$${\mathcal{N}(0, 1)}$$に収束します。これは上図からも分かるように、ｔ分布の自由度が大きくなるにつれ分布の形が鋭くなり、裾野が狭くなっていきます。
ここで考察を深めていきます。前編における分散既知のＺ検定では、検定統計量が

$$
{T(X_1, X_2, …, X_n) = \frac{(\overline{X}-\mu)}{\sqrt{\frac{\sigma^2}{n}}}}
$$

というように既知の分散の値を使っていましたが、今回は

$$
{T(X_1, X_2, …, X_n) = \frac{\overline{X}-\mu}{\sqrt{\frac{V}{n}}}}
$$

$$
{V = \frac{1}{n-1}\sum_{i=1}^n{(X_i-\overline{X})^2}}
$$

として分散に相当する部分に不偏分散を代入した形になっています。ここで検定統計量が従う分布は分散が既知の場合の$${\mathcal{N}(0, 1)}$$と比較して、分散が未知の場合ではｔ分布となり裾野が広く、ばらつきが大きくなっています。つまり検定統計量に既知の値ではなく推定量を使用したことで検定統計量の不確実性があがったと言えます。

さてようやくですが、【問題２】を実際に解いてみましょう。【問題２】を以下に再掲します。

A国の男性の身長は正規分布に従っていると仮定する。いま、A国の男性を$${6}$$人連れてきたところ、身長が$${182, 177, 171, 175, 180, 183\text{ cm}}$$であった。このとき、A国の男性の平均身長が$${173\text{ cm}}$$か否か検定せよ。

【問題２】

Pythonのscipy.statsには１標本ｔ検定を行う関数が備わっていますが、ひとまずここは原理に従ってベタ打ちしていきたいと思います。以下のコードで分散未知の１標本ｔ検定を行うことができます。

#モジュールのインポート
import numpy as np
import scipy.stats as sts
import matplotlib.pyplot as plt
import math
#帰無仮説下での正規分布のパラメータ
mu = 173 #平均
#データ
X_array = np.array([182, 177, 171, 175, 180, 183])
n = len(X_array)
#検定統計量
X_mean = X_array.mean() #平均
V = ((X_array-X_mean)**2).sum()/(n-1)  #不偏分散 Tx = (X_mean-mu)/math.sqrt(V/n) #Zの計算

#p値の計算
p = (1-sts.t(df=n-1).cdf(Tx))*2
print(p)

実行すると$${0.043536…}$$と表示されるかと思います。つまり今回、平均身長が$${173\text{ cm}}$$であるという帰無仮説$${H_0}$$は棄却されました！ただ先ほども書きましたが、このｔ検定は以下のようにscipy.statsで非常に簡単に行うこともできます笑。

#モジュールのインポート
import scipy.stats as sts
#帰無仮説下での正規分布のパラメータ
mu = 173 #平均
#データ
X_list = [182, 177, 171, 175, 180, 183]
p = sts.ttest_1samp(X_list, mu)[1]
print(p)

実行すると$${0.043536…}$$と表示され、先ほどと同様になります。今まで何となく使用していたｔ検定の中身が少しわかるようになってきたのではないでしょうか？
さて、ここで【問題１】の一般的な例における解答を示していきたいと思います。

母集団分布が正規分布に従っているとするとき、その分布から得られた標本$${X_1, X_2,…  X_n}$$を用いて母集団分布の平均が$${\mu}$$に等しいか検定せよ。

【問題１】

という状況においては、

不偏分散$${V = \frac{1}{n-1}\sum_{i=1}^n{(X_i-\overline{X})^2}}$$としたとき検定統計量$${T(X_1, X_2, …, X_n) = \frac{\overline{X}-\mu}{\sqrt{\frac{V}{n}}}}$$は自由度$${n-1}$$の$${t}$$分布に従う。よって$${T(X_1, X_2, …, X_n)}$$にデータから得られた値を代入して得られた値を$${T}$$としたとき、自由度$${n-1}$$の$${t}$$分布において$${T}$$以上（or 以下）の値をとる確率の倍を$${p}$$値とし有意判定をする。

が解答例になります。１標本の平均の検定（分散未知）だけでかなりの分量になってしまったので、最も皆さんが使用するかもしれない２標本のｔ検定は後編に回したいと思います。ここまで読んでくださりありがとうございました！

次回後編もよろしくお願いします！

（2023/08/03 追記）後編は以下になります！

【更新履歴】
2023/07/23 初稿
2023/08/03 後編追加