平均と標準偏差の話

Makersideブログの方で、「原子力発電の必要性について考える」という記事を執筆しました。

昨今言われている原発再稼動については賛否あると思いますが、いずれにせよ、自ら１次情報にあたって、調べた上で事実に基づいて考えることの大切についてお伝えしたかったというのが主旨です。

さて、１次情報にあたるとどうしても、数値データと向き合う機会が増えます。

数値データから正しく情報を読み解くには、データの”調理方法”を知っておく必要があります。

平均と標準偏差というのは、データの調理方法として最も基本的なものの１つですので、今回はこれらについてみていきましょう。

平均

平均はよく知られている統計データなので、説明するまでもないかもしれません。

たとえばボーリングで点数を競い合ったとします。もし「総得点」で競うとした場合、チームAが3人、チームBが4人だと、完全にチームBの方が有利になってしまいますね。

そこで、平均が意味をなしてきます。
平均というのは、データ値を全て合計し、データ数で割ることで求められます。式にすれば

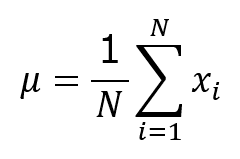
ということになります。
数学記号になれていない人は、いきなりこれを見るとひるんでしまうかもしれませんが、逆にこの式が平均を表すものだとわかれば、記号の意味を理解しやすいかもしれません。

Σというのは、「合計する」という意味を表す記号です。
xiというのは、あるデータを代表した記号で、iというのも、自然数（1,2,3…）を代表させた記号です。
ですから、1/N以外の部分というのは、「iに1からNまでを入れて合計する」という意味で、x1+x2+・・・+xNということになります。
1/Nというのは、1/Nを掛けるとも言いますし、Nで割るとも言えますね。
つまり、データ値を全て合計し（x1+x2+・・・+xN）、データ数で割っているわけです（x1/N）。

先ほどのボーリングの例では、チームAの得点が120、131、92であれば、x1=120、x2=131、x3=92（順番はどうでもいいですが）、N=3なので、平均は（120＋131＋92）÷3＝114.3点　ということになります。

標準偏差

標準偏差という言葉自体、数学アレルギーのある人からすると目をそむけたくなるものかもしれませんが、あまり難しく考える必要はありません。

標準偏差は、「データのばらつき」を表す統計量です。

たとえば先ほどのボーリングの例で、今度はチームBの得点が115、72、81、215だったとします。

この時、平均を計算すると（115+72+81+215)÷4=120.75点　となり、チームAの114.3点を上回ったので、チームBの勝ちということになります。

でも、1人1人の得点を見ると、チームBには72点だったり81点だったり、明らかにチームAのメンバーより得点が悪く足を引っ張っている人がいます。
それにも関わらずチームBが勝利しているのは、チームBの215点の貢献が大きかったからに他なりません。

チーム戦はチーム戦ですが、チームAの皆さんからすれば面白くないですね。

こんな時、単に平均値で比較するのはフェアではなさそうです。そこで、標準偏差の出番です。

標準偏差というのは、各データが、平均からどれだけばらついているかを数値化した統計量です。

どういうことか、次は違う例でみてみましょう。

A君とB君は同じ陸上競技部に所属していて、二人とも100m走の選手です。

あるシーズンで、A君のタイムは試合ごとに10.57秒、10.98秒、10.77秒、10.60秒だったとします。一方のB君は、10.02秒、10.98秒、11.32秒、10.40秒だったとします。

さて、どちらのパフォーマンスが良いでしょうか？ということです。

まず平均を出すと、A君は(10.57 + 10.98 + 10.77 + 10.60)÷4 = 10.73秒、B君は(10.02 + 10.98 + 11.32 + 10.40)÷4 =  10.68秒で、B君の方が成績がよさそうです。

ただ、”パフォーマンス”という意味ではどうでしょう。

B君は9秒台に迫るときもあれば、11秒を切れないときもあり、タイムが安定していなさそうです。

たしかにベストの記録はB君の方が上ですが、全体を見ると、A君の方が安定して10秒台で走れており、パフォーマンスは安定してそうです。

こんなときに、標準偏差の出番です。

A君の個々のタイムが平均とどれだけ差があるかというと
10.57 - 10.73 = - 0.15秒、10.98 - 10.73 = 0.25秒、10.77 - 10.73 = 0.04秒、10.60 - 10.73 = - 0.13秒

B君の個々のタイムが平均とどれだけ差があるかというと
10.02 - 10.68 = - 0.66秒、10.98 - 10.68 = 0.30秒、11.32 - 10.68 = 0.64秒、10.40 - 10.68 = - 0.28秒

では、Ａ君とＢ君、どちらがパフォーマンスが安定しているか、つまり、どちらの方がタイムのばらつきが小さいかは、どうやって見てみればよいでしょうか。

試しに、いま計算した平均からの差を、全部足し合わせてみます。
すると、Ａ君は{- 0.15 + 0.25 + 0.04 + (- 0.13)} = 0.01秒、Ｂ君は{- 0.66 + 0.30 + 0.64 + (- 0.28)}÷4 = 0秒となり、僅差ですが、この計算だとＢ君のタイムの方がばらつきが小さいように見えます。

これで良いのでしょうか。

もっとわかりやすい例で、たとえばC君とＤ君が100点満点のテストを4回受けて、Ｃ君が50点、50点、50点、50点だったのに対し、Ｄ君が0点、100点、0点、100点だったとします。

Ｄ君の方が点数のばらつきがあるのは明らかですね。

しかし、先ほどと同じように計算すると、Ｃ君もＤ君も平均点は50点なので、個々の点数の平均からの差分は

Ｃ君の場合、50 - 50 = 0、50 - 50 = 0、50 - 50 = 0、50 - 50 = 0なのに対し、Ｄ君の場合 0 - 50 = -50、50 - 50 = 0、0 - 50 = -50、50 - 50 = 0となり、それぞれ全部足し合わせるとＣ君は0点、Ｄ君も0点となります。

この計算では、ばらつきをちゃんと表現できていないことになります。

何がまずかったかというと、マイナスを許してしまったことです。

たとえば、Ｄ君の点数で平均からの差を計算するときに、0 - 50 = -50としたことです。

平均からの差を表現するのにマイナスを許していると、先ほどのＤ君の例のとおり、平均からいくらばらついていても、プラスとマイナスを足し合わせることで打ち消し合ってしまいます。

なので、マイナスを使わずに平均からの差を表現する必要があります。

単に平均からの差の絶対値を取る（たとえばD君の例では、|0 - 50| = 50点とする）という方法も考えられますが、結論からすると、ばらつきは次のように定義されます。 

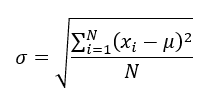
せっかくいい感じについてこれたのに、この式を見て突き放された感を覚えた方もいるでしょう。

でも冷静に見ると、先ほど平均の定義式で確認した記号の応用です。

xiは個々のデータ値、μはデータ全体の平均、Nはデータ数なので、A君の例でいうと、次のような計算をしています。

√[{(-0.15)^2 + 0.25^2 + 0.04^2 + (-0.13)^2}/4] = 0.161

B君も同じように

√[{(-0.66)^2 + 0.30^2 + 0.64^2 + (-0.28)^2}/4] = 0.503

と計算できます。今度は、B君の方が大きい値になっていますね。

このように計算されたσを、標準偏差と呼びます。

(xi - μ)^2というのは、個々のデータの平均からの差を2乗していることになります。2乗する理由は、マイナスをなくすためです。

Σ(xi-μ)^2で、(xi-μ)^2をi=1 ~ Nとして足し合わせています。つまり
(x1-μ)^2 + (x2-μ)^2 + ・・・ + (xN-μ)^2です。

それをデータ数Nで割るということは、個々のデータの平均からの差の2乗和を平均していることになります。

言葉で書くとわかりづらいですね。

最後にその値に対して平方根（√）を取っています。
これは、単位を元通りにするためです。

どういうことかというと、たとえばA君について

{(-0.15)^2 + 0.25^2 + 0.04^2 + (-0.13)^2}/4

を計算すると0.0259となりますが、-0.15や0.25といった値の単位は「秒」なので、それを2乗して足し合わせたものの単位は「秒の2乗」になります。

タイムは「秒」なので、ばらつきも「秒」で表しておいた方が同じ土俵で扱えて都合が良いのです。なので、「秒の2乗」の平方根を取って、「秒」に直しています。

まとめ

以上、データ調理法の基本として、平均と標準偏差についてみてみました。

• 平均は、データ値の代表値を表す指標の1つ。データ値を全て足し合わせた後、データ数で割ることで求められる

• 標準偏差は、データのばらつきを表す指標の1つ。個々のデータの平均からの差の2乗和を平均したのち、平方根を取ることで求められる。