
二乗の和の公式 〈証明〉
二乗の和(Σk^2)の公式とは、このような式である。
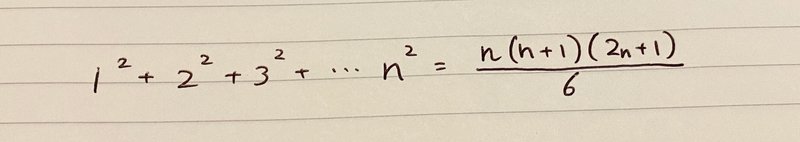
〈証明〉
一辺の長さが1の立方体を積み上げることを考える。
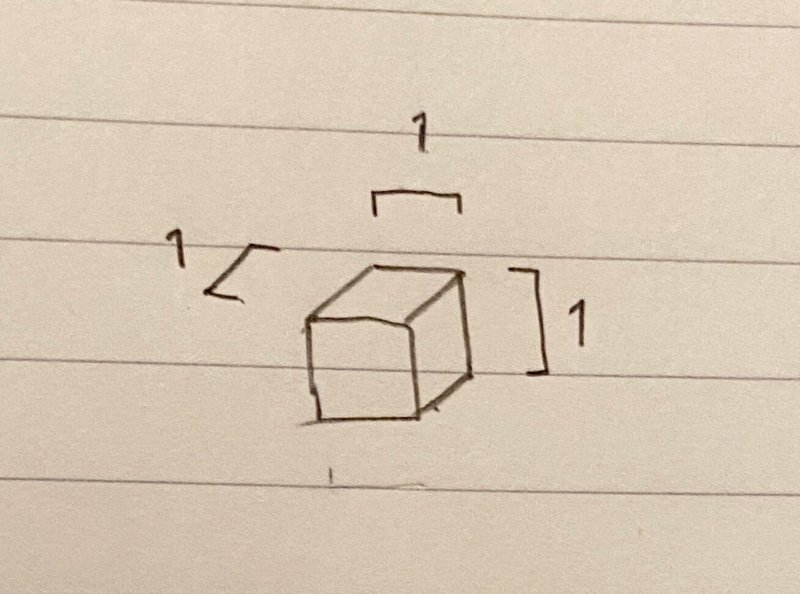
下の絵のように高さがn段のピラミッド状に積み上げる。
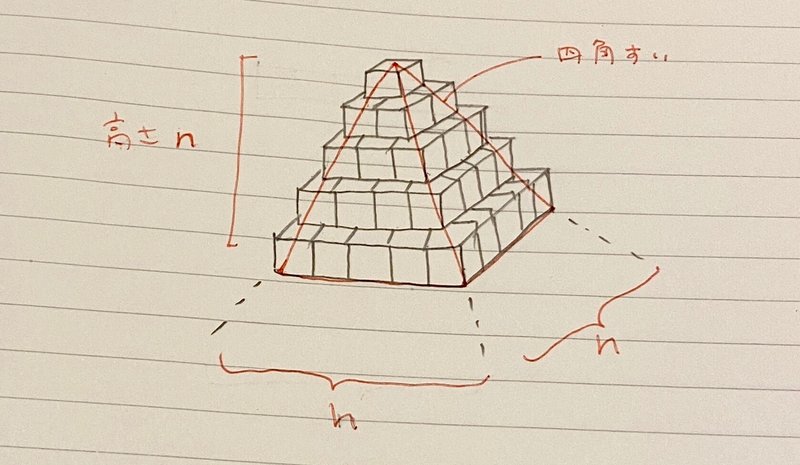
このn段積み上げたピラミッドは、一段目が1つ、二段目が4つ、三段目が9つというようになって、n段目では(nの二乗)個となる。
つまりこのピラミッドに使われる立方体の個数が二乗の和(Σk^2)になることは自明である。
ここで私は、そのピラミッドにすっぽりおさまる「四角すい」を考え、その四角すいに余りの部分を足し合わせることによってピラミッドの体積を求めようとする。
すぐには意味が分からないかもしれないが、
ピラミッドの体積=四角すい+1段目の余り分+隅の余り分+辺の余り分
という式が成り立つ。繰り返すが、ここでこの式の意味がわかる必要はない。ざっくりと読み進めてほしい。
ここからは、右辺の一つ一つを足し合わせることによりピラミッドの体積を求めることが目標である。
①四角すいの体積
n段目まで積み上げたピラミッドにすっぽりおさまる四角すいの体積を求める。これは簡単である。
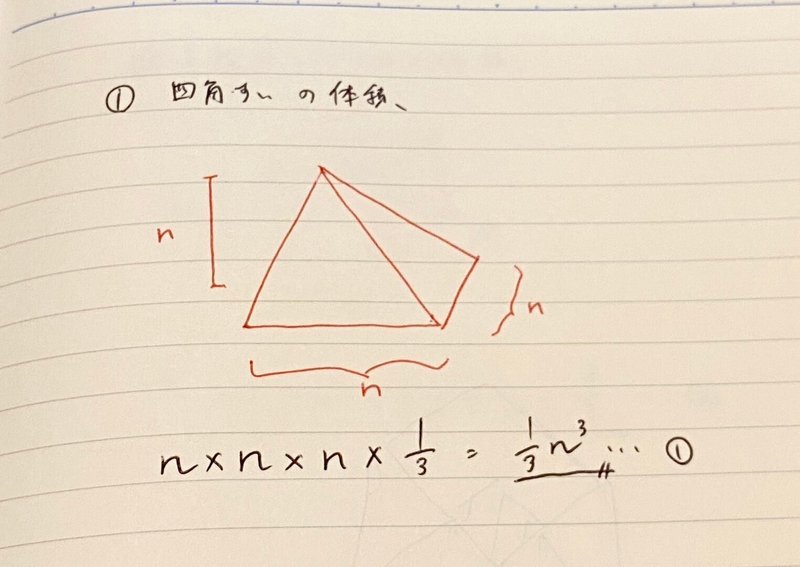
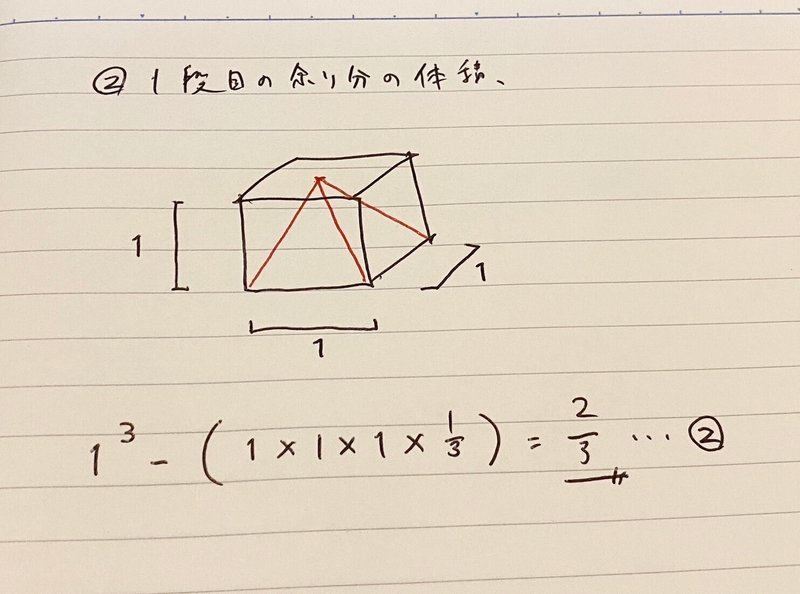
②1段目の余り分の体積
1段目の余り分(四角すいからはみ出している部分)の体積を求める。これも簡単である。
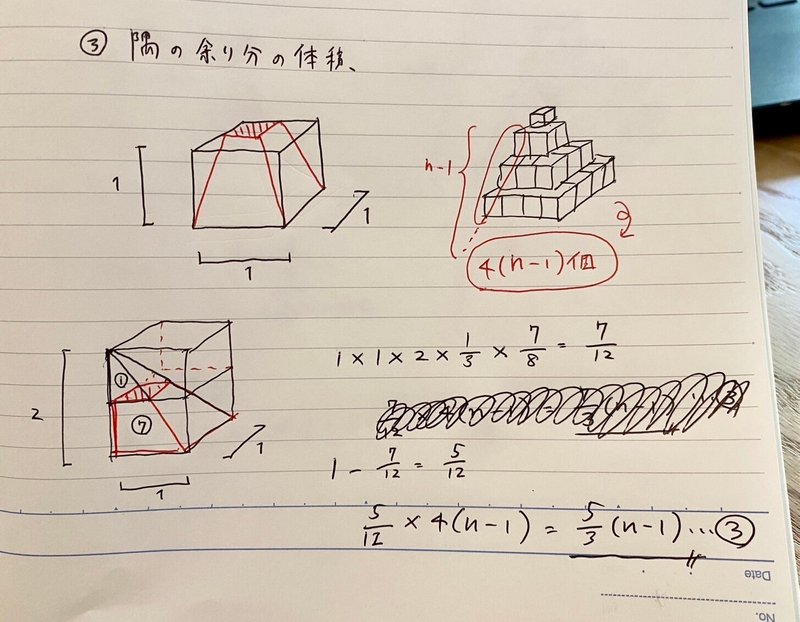
③隅の余り分の体積
次に、隅の余り分(四角すいからはみ出している部分)の体積を求める。
これは少し難しいが、上に伸ばして「四角すい」の形にしてから、相似の性質(1:2の相似な立体は体積が1:8になるという性質)を利用してもとの体積を求めている。
※ピラミッドからはみ出した部分の体積を求めているので1から7/12を引いている。
また、隅のパーツがいくつあるかどうかにも注意する必要がある。隅のパーツは4(n-1)個ある。
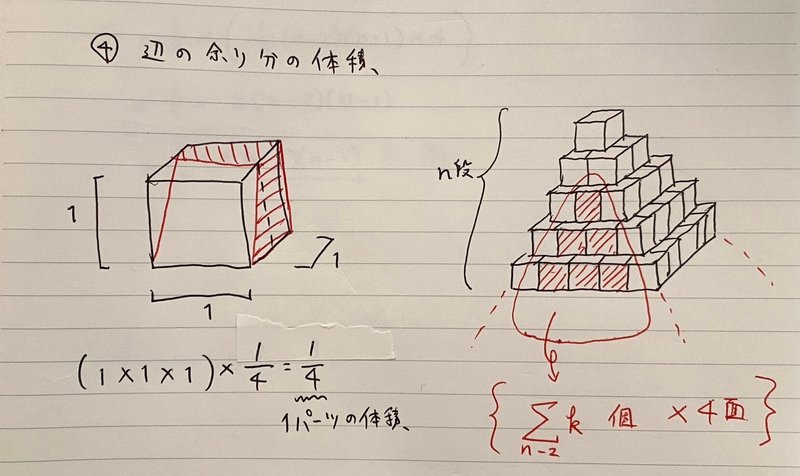
④辺の余り分の体積
最後に、辺の余り分(四角すいからはみ出している部分)の体積を求める。
これも少し難しい。
※ピラミッドからはみ出した部分の体積を求めているということに注意する。
個数を求める際には、和の公式(Σkの公式)を用いる。
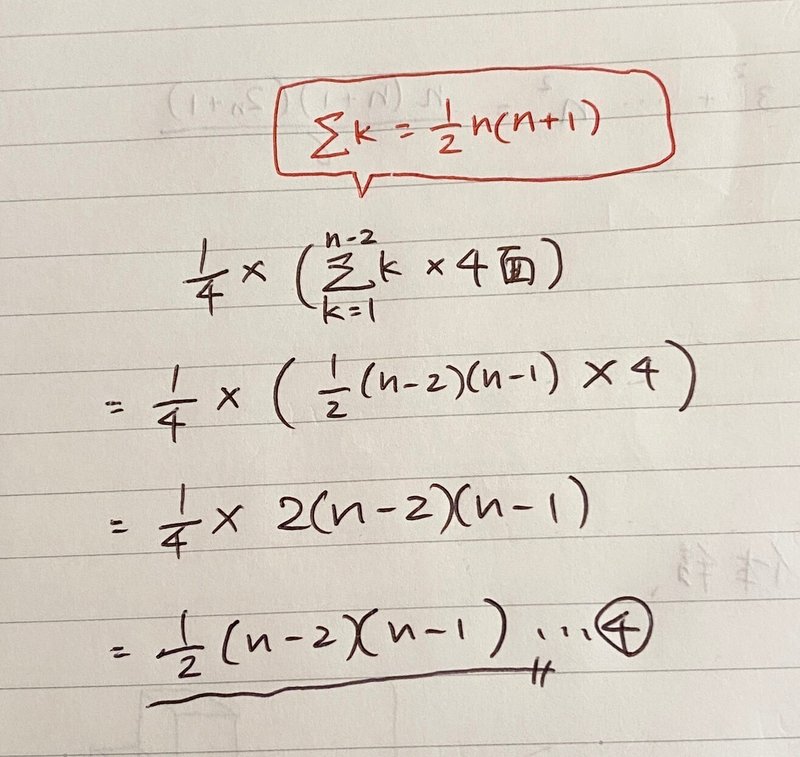
改めて最初に示した式を載せる。
ピラミッドの体積=四角すい+1段目の余り分+隅の余り分+辺の余り分
これまでに求めた①~④で、上式の右辺がすべて求まったのでそれらを足し合わせる。
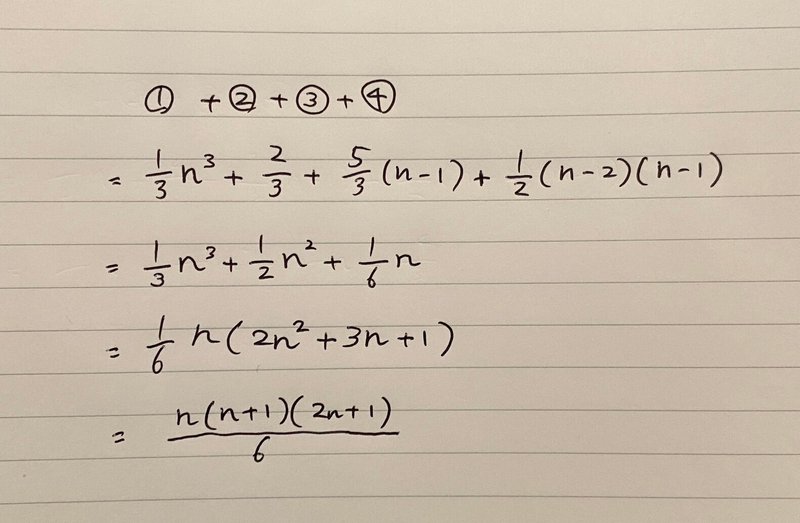
このようにして、n段目まで積み上げたピラミッドの体積を求めることができた。そして、ピラミッドの体積が「二乗の和」になることは自明なので、これにて証明終わりである。
この記事が気に入ったらサポートをしてみませんか?
