[R,Onyx]共分散構造分析①
共分散構造分析は、観測された変数や、それらによって構成される概念の関係を扱う分析手法です。最大の特徴はその柔軟性で、因子分析、主成分分析、重回帰分析といった多変量解析を拡張することができます。
また、構造が複雑になっても、パス図によって視覚的に分かりやすく示すことができるというのも大きな特徴です。
因子分析や重回帰分析などをあわせて記述することも可能です。
1.モデル表現
記号を使って書き表すのですが、そこには決まりがあります。
■矢印の種類
矢印には、大きく分けて一方向の矢印(→)と双方向の矢印(↔)があります。前者は因果関係、後者は相関関係を示しています。ここでは書かれていませんが、分析結果を示すパス図の場合、矢印にはパス係数と呼ばれる数字がふられます。パス係数は、因果関係の場合には回帰係数、相関関係の場合には相関係数となります。

■変数の種類
変数の種類には、大きく3つの観点で6種類があります。
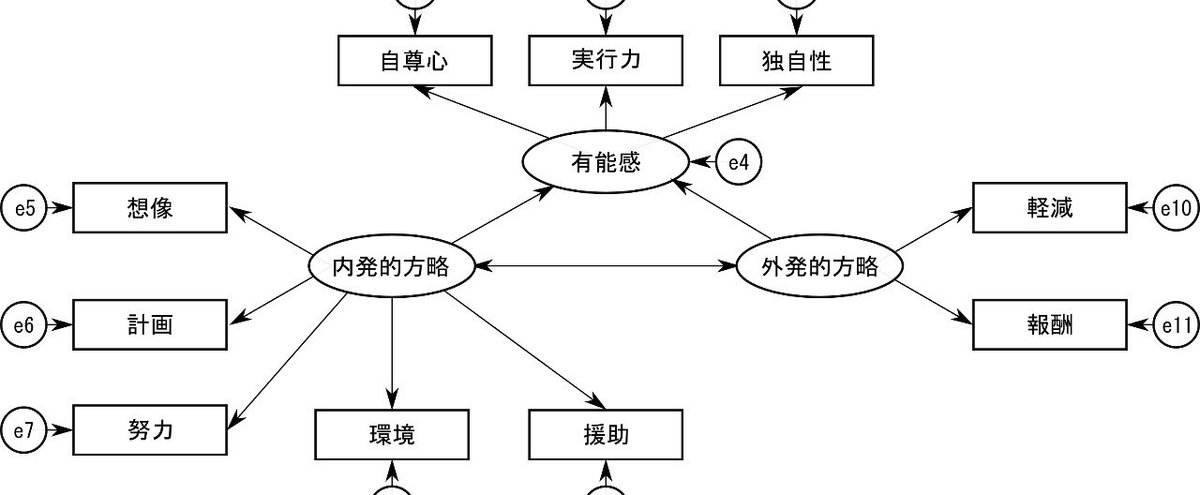
・観測変数と潜在変数:観測変数は、直接測定できる変数で、質問紙の質問項目つまり因子分析での項目などがこれにあたります。潜在変数は、直接測定できない想定上の変数です。因子分析の因子、主成分分析の主成分などがこれに当たります。パス図では、観測変数は四角、潜在変数は楕円または円で表します。先の図であれば、「同一化動機」「内発的動機」は観測変数、「自律的動機」は潜在変数です。
・構造変数と誤差変数:構造変数は、直接考察の対象となっている変数で、観測変数と潜在変数がこれに当たります。誤差変数は、分析に用いた構造変数以外で変動の原因となっていると想定される要因です。直接測定されているわけではないので、誤差変数は潜在変数となります。パス図では、誤差変数は小さな円で描かれることが多いです。先の図では「e1」から「e13」が誤差変数です。
・外生変数と内生変数:外生変数は、モデルの中で一度も他の変数の結果とならない、つまりパス図で一度も単方向の矢印を受けない変数です。モデル上で他の変数の影響によって変動しないので、その変動がモデルの外部にある要因によるところから外生変数と呼ばれます。内生変数は、モデルの中で少なくとも一度は他の変数の結果となっている、つまりパス図で少なくとも一度は矢印を受ける変数です。モデルの内部でその変動が説明されるので内生変数と呼ばれます。内生変数には必ず誤差変数をつけなければいけません。先の図では「自律的動機」と「他律的動機」は単方向の矢印を受けていないので外生変数となり、他はすべて内生変数です。
■測定方程式と構造方程式
測定方程式と構造方程式は、変数間の関係を示します。これらは内生変数ごとに立てられます。
・測定方程式:潜在変数が複数の観測変数に影響を与えている様子を表すための方程式です。先のパス図の①の部分「同一化動機」「内発的動機」「自律的動機」の関係は、測定方程式で記述されます。測定変数である「同一化動機」「内発的動機」への「自律的動機」からの影響にはパス係数として回帰係数が存在しますから、
・構造方程式:変数間の因果関係を表すための方程式です。「潜在変数が他の潜在変数の原因となる」「観測変数が他の観測変数の原因となる」「観測変数が潜在変数の原因となる」という3つの関係が存在します。先の図では、「有能感」と「自律的動機」「他律的動機」の関係は「潜在変数が他の潜在変数の原因となる」関係で、②の部分は「観測変数が他の観測変数の原因となる」関係です。「有能感」と「自律的動機」の関係を式で表すと、
自律的動機=係数3×有能感+誤差3
となります。
2.観測変数を用いたモデル
質問紙で文系、理系、外国語のセンスを問い、その結果と数学のテスト成績の関係をモデルに表してみると、各センスから数学のテスト成績への影響がある一方で、センス間には相関関係が想定されるでしょう(外国語も文系科目も文章理解の点では共通点があるし、文の構造などを理解する力は理系の論理的な考え方と通じるところがある、など)。
影響関係は回帰分析で、相関関係は相関係数を求めることで、それぞれ分析することができますが、パス解析ではその2つの関係を同時に見ることができます。
それをパス図に表してみると、次のようになるでしょう。

ここでは、Ωnyx(以下、Onyx)というソフトウェアとRのlavaanパッケージを用いて分析を行います。
■パス図の作画
Onyxを起動すると、空っぽのウインドウが開くので、
・[Ωnyx]→[Create Empty Model]を選択。
そうすると、空のシートが現れます。ここのシートは、右クリックメニューの[Customize Model]から、
[Change Grid Propaties]→[Display Grid]で、グリッド表示に切り替えています。
また、[Change Grid Propaties]→[Lock to Grid]で変数をグリッドに合わせて移動させることができます。

[Ωnyx]→[Load Model or Data]を選択し、データファイルを選択します。

・データのヘッダが一覧で表示されます。

このデータでは「x1」から「x3」が、順に文系、理系、外国語になっています。また、数学のテストの成績が「M」に入っています。
・「x1」「x2」「x3」「M」をシート上にドロップし、位置を整えます。

ここでは、元のパス図を90度回転させた状態で作図しています。変数についている双方向の曲がった矢印は、分散や誤差分散です。
・原因となる変数上で右クリックをし、そのまま影響を受ける変数までドラッグして、パスを引く。
・原因となる変数上で右クリック・メニューを表示し、[Add Path]を選択、影響を受ける変数上で左クリックでも同様にパスを引くことができる。

・パス上で右クリック・メニューを表示し、[Toggle Rath Heads]を選択すると、矢印の向きが反転する。もう一度同じ操作をすると、双方向の矢印になる。
・双方向矢印は、選択状態にすると緑のガイドが表示されるので、先端の○をドラッグして動かすことで、パスを変形させることができる。
・パス上で右クリック・メニューを表示し、[Free Parameter]を選択する。係数が自由母数であるパスはすべてこの操作を行う。

実はこの時点で一応推定は行われていて、パスには非標準化係数が表示されています。パス上で右クリック・メニューを表示し、[Customize Path]→[Show Standardized Estimates]を選択すると、標準化係数を表示することができます。
また、右クリック・メニューを表示し、[Show Estimate Summary]を選択すると、推定結果の詳細を見ることができます。
さらに、他のソフトウェアで詳細な処理するためのスクリプトを書き出すことができます。ここでは、Rのlavaanパッケージ用のスクリプトを書き出してみます。
・シート上で右クリックメニューを表示し、[File]→[Export Script]→[lavaan]を選択。

・適当な名前をつけてスクリプトを保存する。
このパス図の場合、下のようなスクリプトが保存されます。
ただ、このままでは使用できないので、書き換える必要があります。

■Rでの分析
書き出されたスクリプトを、必要に応じて書き換えて分析に使用します。ここでは、以下のように書き換えました。太字にした部分が変更箇所です。
1 #
2 # This model specification was automatically generated by Onyx
3 #
4 Library(lavaan);
5 modelData <- as.data.frame(scale(read.csv("E:/PSPP_DEMO/SEM/sense1.csv", header = TRUE)))
6 model<-"
7 ! regressions
8 M ~ x1__M*x1
9 M ~ x2__M*x2
10 M ~ x3__M*x3
11 ! residuals, variances and covariances
12 x1 ~~ VAR_x1*x1
13 x2 ~~ VAR_x2*x2
14 x3 ~~ VAR_x3*x3
15 M ~~ VAR_M*M
16 x2 ~~ COV_x2_x1*x1
17 x3 ~~ COV_x3_x2*x2
18 x3 ~~ COV_x3_x1*x1
19 ! observed means
20 x1~1;
21 x2~1;
22 x3~1;
23 M~1;
24 ";
25 result<-lavaan(model, data=modelData, fixed.x=FALSE, missing="FIML",estimator = "ML",fixed.x = FALSE);
26 summary(result, fit.measures=TRUE,rsquare=TRUE);
27 standardizedSolution(result)
5行目は、データの読み込みです。read.csvで、ローカル上のファイルを指定し、scale関数でデータを標準化、as.data.frame関数で、データフレーム形式に変更しています。
25行目では、「estimator = "ML"」で推定方法として最尤推定法を指定しいています。「fixed.x = FALSE」で、変数の平均、分散、共分散を自由パラメータとして指定しています。このモデルの場合、指定をしなくても分析はできますが、「fixed.x = FALSE」とするよう警告がでます。また、ここでlavaan()関数の変わりにsem()関数を使うことも可能です。
26行目は、結果の表示ですが、「rsquare=TRUE」とすることで重相関係数の平方(決定係数R2)を表示するように指定しています。
27行目で、結果を標準化して表示しています。
■出力の見方
見るべきところはたくさんありますが、まず標準化した結果から確認しておきます。

1行目から3行目が、数学の成績(M)に対する文系(x1)、理系(x2)、外国語(x3)の影響で、[est.std]が標準化された係数です。[se]は標準誤差、[z]はz値、[pvalue]はp値です。
7行目が数学の誤差変数です。
8行目から10行目が、文系、理系、外国語の相関関係を示しています。
summary関数で表示される内容は次のようになります。長くて見難いですがお付き合いください。

観測対象数つまりデータのケース数(Number of observations)が1160件、推定方法(Estimator)が最尤推定法(ML)です。
以下、χ2値(Minimum Function Test Statistic)912.448、自由度(Degrees of freedom)6、p値(P-Value)0.00などと示されています。
それ以下の部分には、適合度指標が続きます。
Comparative Fit Index (CFI)比較適合度指標 は、0から1の間の値を取り、数値が大きい方が適合度が高いと考えます。0.95以上あればよいモデルだと判断されます。
Tucker-Lewis Index (TLI) Tucker–Lewis 指標もCFI同様に、1に近い方がよいと判断できる数値ですが、1以上の値をとる場合もあります。
Akaike (AIC)は赤池情報量基準で、モデルを比較する場合の相対的評価基準です。比較した中で数値が小さい方がよいモデルと判断します。
Bayesian (BIC) ベイジアン情報量基準、Sample-size adjusted Bayesian (BIC) サンプルサイズ調整済みベイジアン情報量基準も、AIC同様、相対的な比較基準で、最も値の小さなモデルがよいモデルと判断されます。
RMSEA(Root Mean Square Error of Approximation)平均二乗誤差平方根は、一般に0.05以下であればあてはまりがよく、0.1を超えるとあてはまりが悪いと判断されます。
SRMR(Standardized Root Mean Square Residual)標準化残差平均平方は、下限が0で、0に近いほどあてはまりがよいと判断します。
Regressionsの部分は構造方程式の係数をしめしています。先ほどの標準化した結果の1行目から3行目に相当します。
Covariancesは、共分散に関する推定結果で、先の標準化した結果の8行目から9行目に相当します。
Interceptsは、切片パラメータです。先の標準化した結果の11行目から14行目に相当します。
Variancesは分散の推定結果です。先の標準化した結果の4行目から7行目に相当します。
R-Squareは、重相関係数の平方(決定係数R2)です。
以上の結果を、パス図に書き込むと次のようになります。

上の図は、RのsemPlotパッケージに含まれているsemPaths関数を用いて作図したものを、SVGで書き出し、ドローソフトinkscapeで微調整しています。
ここでは、以下のような設定で出力しています。
semPaths(result2, whatLabels = "stand", #標準化
layout = "tree", #レイアウトの指定
style="lisrel", # LISREL型の図
sizeMan = 10, #観測変数の大きさ
rotation = 2,#回転
edge.label.cex=1,#フォントの大きさ
edge.color = rgb(red = 0,green = 0,blue = 0,maxColorValue = 255),#白黒
nodeLabels = c("数学","文系","理系","外国語"),
fade = F, #パスを薄くしない
intercepts = FALSE)#最低限の表示
この結果を見ると、3つのセンスは互いに高い相関関係があることが分かります。特に外国語と文系の相関が高くなっています。センスと成績の関係では、外国語と文系は数学の成績に対してほとんど何の影響も与えていないことが示されています。それに対して、理系は影響していると言えます。
ただし、誤差からの係数が0.90あるので、他の要因からの影響の方が遥かに大きいと言えます。しかし、テスト成績は、学習の仕方や時間、出題範囲、体調など様々な要因が影響していると考えられますから、それは当然と言えるでしょう。
※ここでは、lavaanパッケージとsemPlotパッケージを用いていますので、「R」に両パッケージをインストールし、分析前に読み込んでおく必要があります。
インストールされていない場合は、
install.packages("lavaan")
install.packages("semPlot")
の2つのコマンドを実行しておきます。これは一度行うだけでよく、分析のたびに行う必要はありません。
ただし、「R」にパッケージを読み込む、
Library(lavaan)
Library(semPlot)
は、「R」起動後の分析前に1度は行っておく必要があります。1度読み込むと、「R」を閉じるまでは有効です。
