人材選抜にかかわる人の基礎知識（統計編２）

前回に引き続き、人材選抜や人事・試験等にかかわる人が、知っておくと便利な統計的基礎知識をわかりやすく説明していきます。

標準得点

試験の得点は、一般的に、中央くらいの数値に一番人数が集まり、その点数より、高い受験者や、低い受験者は、その中心から離れるほど人数が少なくなる傾向が見られます。こうした分布をうまくモデル化したものが「正規分布」です。
正規分布とは理論的に導かれた分布で、これを曲線のグラフで表すと中央の部分が最も高い左右対象の形になります。実際の選抜試験の得点分布が、この正規分布に完全に重なるわけでは無いのですが、統計的にこの特徴を利用すると次のようなことがわかります。

（特に選抜試験との関係でいえば、）平均点と平均点から１標準偏差離れたところに受験者全体の34.1%が含まれるので、平均点から点数の高い方及び低い方にそれぞれ１標準偏差離れた部分に68.3%の受験者が含まれることになります。
さらに、高い方及び低い方に２標準偏差離れた部分に95.4%の受験者が、３標準偏差離れた部分に99.7%の受験者が含まれることになります。

例えば、数学と英語からなる選抜試験を行った結果が、次のようになったとします。

受験者Aは難しい数学のテスト（受験者全体の平均点は30点、標準偏差は10点）で60点、比較的易しかった英語のテスト（受験者全体の平均点は60点、標準偏差は28点）で平均点と同じ60点をとったとします。
一方、受験者Bは同様のテストで数学は32点（平均点は30点）、英語は88点（平均点は60点）でした。
　           数学  英語  合計点
A(素点）  60　 60 　120
B(素点）  32　 88　 120
平均　     30     60 　
標準偏差 10     28 　

このとき単純に数学と英語の得点の合計では、受験者AもBも、120点ですので、素点の合計だと同じ評価になります。

しかし、Aは難しい数学のテストで平均の二倍の点数をとり、標準偏差が10ですから、2標準偏差分上位になっています。これは、正規分布で考えると、上位5％に入っている可能性があります。他方、英語は平均点です。

Bは、数学は平均点に近い点数ですが、英語は平均より28点高く、これは(英語の点でみると)1標準偏差高い点数です。

このような場合の考え方として、「標準得点」という考え方があります。それぞれの試験の平均と標準偏差が分かっている場合は、これらの数値を用いて、平均を50点、標準偏差を10点に変換するもので、次の式で示されます。

このように、標準得点を求めると、Aの数学は80点に、英語は50点に換
算され、Bの数学は52点、英語は60点に換算されるので、それぞれの合
計点は130点と112点と違いがはっきりしてきます。

　　　　　　　数学　 英語　 合計
Ａ(標準得点） 　80        50      130
Ｂ(標準得点）     52        60      112

素点で見ると同じ点数でも、それぞれの選抜試験の平均点や標準偏差の
異なりを考慮して「標準得点」を算出すると、結果は異なってくるのです。
そのため、特に異なる種類の選抜試験を行って、それらの合計を算出する際には、単に素点の合計ではなく、「標準得点」に換算して合計することが大切です。

これらの標準得点への換算のイメージ表したものが次の図になります。二つのテストＡとＢがあり、Ａはほぼ正規分布しているテスト、Ｂは（比較的易しいので）高い点数に偏った分布とします。もちろん両者の平均得点（平均点）と偏差は異なります。これを標準得点に換算したものが下の図になります。(両者とも平均は50点、標準偏差は10に変換されました。）

標準得点への変換は、このように、単に各試験の素点で点数を扱うよりも、より受験者の能力を正しく測定することに役立つのです。実際の選抜試験では次のようなことも考えられます。

例えば、第1次試験で、ある試験を標準得点化し、そのうち、一定の点数を取った者(点数の高かった者)のみが、第2次試験に進み、別の試験を受けたとしましょう。

その際、第1次試験と第2次試験の標準得点化について、一般に第1次試験は受験者全員が受けるので、標準偏差（分散）は大きくなる傾向があります。一方、第2次試験では特定の点数以上の者の少数が試験を受けるので、標準偏差が小さくなる傾向があります。
次の式で標準得点が算出されますので、第1次試験のように標準偏差が大きくなれば、相対的に(分母が大きくなるので)点数は低く見積もられます。他方、第2次試験のよう標準偏差が小さくなれば、相対的に(分母が小さくなるので)点数は高く見積もられます。

すなわち、第2次試験の(標準点化された)1点は（第1次試験のように全員が受験した時よりも）高く算出されることになるので、人数が絞り込まれた第2次試験の1点の差は大きく見積もられるのです。

そのため、厳格な試験では、「第1次試験を受けた全受験者のうち、第2次試験を受けた受験者の標準偏差を利用して」第2次試験の標準得点を新たに推定する方法もあるのです。

相関係数

相関とは、二つのデータの関連性を示す指標の一つです。例えばテストAとテストBがあり、テストAが出来た人ほどテストBの得点も高ければ、「正の相関がある」とされ、逆に、テストAが出来た人ほどテストBの得点が低ければ、「負の相関がある」とされます。
図表は、テストAとテストBの散布図と、テストAとテストCの散布図を示したものです。
テストAとテストBは、「正の相関がある」ケースで、テストAとテストCは「負の相関かある」ケースとなります。

一般的に相関係数は、アルファベットの ｒ で表し、
相関係数 ｒ は、必ず -1 ≦ ｒ ≦ 1 の範囲で、
1）正の相関があるとき、相関係数 ｒ は正の値をとります（ 0 ＜ ｒ ≦ 1 ）
2）相関が全くないとき、相関係数 ｒ は 0 となります
3）負の相関があるとき、相関係数 ｒ は負の値をとります（ -1 ≦ ｒ ＜ 0 ）
となります。
また、相関係数ｒ が 1 に近ければ近いほど、正の相関は強くなります。

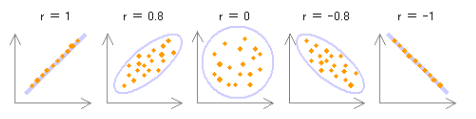
ｒ ＝ 1 となるとき、完全相関といい、プロットされたデータは一直線上に並びます。負の相関も同様に、 -1 に近いほど強くなります。ｒ ＝ -1 の場合も完全相関といいます。
相関係数を求める式は次のようになります。

相関係数の分子Ｓxyにあたるのは、変数x,yの共分散※ と呼ばれる値です。 

※共分散とは「テストAの点数」と「テストBの点数」のような「二組の対応するデータ」の間の関係を表す数値で、共分散を計算することで，「テストAの点数」が高いほど「テストＢの点数」が高い傾向にあるのか。あるいは「テストAの点数」と「テストＢの点数」は関係ないのかなどが分析できます。また、共分散は，「Xの偏差 × Yの偏差」の合計の平均で定義されます。※偏差は平均との差のこと。

（相関係数ｒの）分母は変数x、yのそれぞれの標準偏差を掛けたものです。
共分散はx、yの1組のデータについて、式にあるように、平均点からのズレをそれぞれ掛け算したものをすべて足して、データの個数で割った平均値を求めたものですから、一方が平均点よりも低くなったとき、他方が平均点よりも高くなれば負の値になります。

そして、それらを合算して平均を求めたものが共分散になります。
このときに分母の数値はそれぞれの試験の標準偏差ですから、必ず「正の値」なので、分子の値によって、相関の強さと正･負が数値化される訳です。

相関係数を扱うときには次のようなことに気をつける必要があります。

○直線的関係以外は捉え難い

相関係数は基本的には直線的な関係の強さを表すものであり、曲線的関係は表せません。そのため、相関係数が低いからといって、二つの試験に関連性がないと即断することはできません。

（図のようなケースの場合、相関係数は0（-0.091）に近いですが、散布図をよく見ると、何となくテストAの60点を境に関係がありそうな状況が見てとれます。（テストAの点数が低い者はテストBと正の相関が見られ、60点以上の点数をとる者はテストBと負の相関がみられる）

○相関係数が高いからといって、かならずしも因果関係があるとは限らない

ある「知識テスト」(例えば理科のテスト）とある「体力テスト」（例えば短距離走の速さのテスト）の相関係数が（たまたま）高いからといって、その知識が多い人は体力があると単純に判断することができないように、相関係数から因果関係を導く場合には、いろいろな情報を集めて慎重に判断する必要があります。

○相関係数を扱うときは異常値に注意すること

次の上図（散布図）に示したようなデータの場合、相関係数のみを見てテストDとテストEの相関関係を簡単に判断することは適当ではありません。
このように、それぞれの試験で極端な点数を取った受験者がいる場合は、その影響を受けて相関係数が大きく変化することがあるのです。
このケースの場合は、上のグラフのように（テストEが50点でテストD が25点だった）受験者10の点数が影響して相関係数がマイナス0.77で、高い負の相関があるように思われますが、この受験者の影響を排除すると相関係数はマイナス0.2と相関がないことがわかります。

○相関係数を扱うときは集団の範囲を気をつける必要があること

二つのテストの相関を考えるときに、(場合によっては）第1次試験のテストAと、第2次試験のテストBの関係を考える場合があります。

このときに考えなければならないのは、第1次試験の合格者のみが第2次試験を受けるため、集団の範囲が異なるということです。

次の図に示したように、第1次試験でテストAを行い、その合格者に第2次試験のテストBをするケースですが、上にあるように全員が両方の試験を受けることが出来れば、相関係数は0.87とかなり高いのですが、テストAの60点以上の第1次試験合格者のみでの相関係数は0.51と低くなってしまうのです。
この現象は、選抜試験の結果と採用後の成績の相関を算出する際にも同様の結果が生じ、一般に、選抜試験の結果と採用後の成績の相関が高くなることが予想されるのに関わらず、実際に両者の相関が高く出ない理由の一つでもあるのです。（このような現象は「選抜効果」ともいわれます）

なお、相関係数は、二つのテスト間の関係を示す指標であるため、次の下表にあるように、テストAとテストBの相関係数は、テストAの全ての得点に10点を加えても、全ての得点を二倍にしても、（テストAとテストBの）相関係数は0.78で変化ありません。

今回は、標準得点と相関係数について中心に説明しました。次回も人材選抜・試験にかかわる「あなた」に役立つ知識をお届けしたいと思います。 　　　　　　　　　　　　　　　　　　　　Mr.モグ