31までというと…日にちを数えるのに便利かも？

片手でいくつまで数えられる？

――10！
そう答える人は多いだろう。
親指から順に折りたたみ、全部折れたら小指から順に元に戻す。

――5！
そう答える人は慎重派だ。
数え方は上の10と同じだが、4と6が同じだ！3と7がいっしょだ！との主張。
ごもっとも。

――31！
はい？　なんですと？
上で10すら怪しいという話をしたばかりなのに、31ってあんた。

いや、31も正解！

そのからくりはこうだ。
指をすべて折りたたんだ状態を0として、親指だけ立てて1、次は人差指だけ立てて2、次は親指と人差指を立てて3…と続く。

指をフルに使って数えているのは分かるが、動きが複雑すぎる。
指を立てている状態を「○」、折っている状態を「×」で単純化してみるとこうなる。

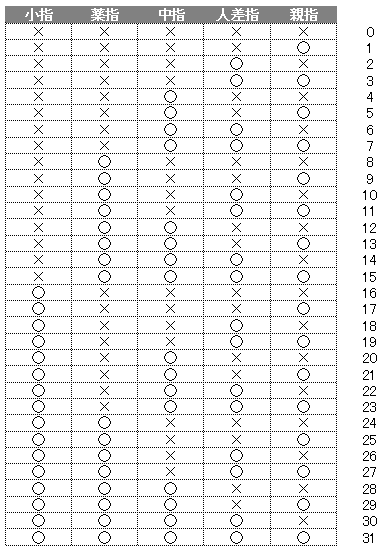
リズムのようなものが見えてきた。
表を縦に見ると、親指は「×○」の繰り返し、人差指は「××○○」の繰り返し、中指は「××××○○○○」の…
うぅむ、これはいったい何だ？

さらに「○」を「1」に、「×」を「0」に書き直してみる。

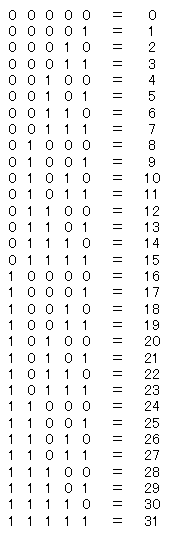
お？　これはもしかして？　そう、2進数だ！

2進数と聞いて頭がズキズキしはじめた方、丁寧に説明するのでもう少しだけおつきあいを。
原理さえ分かればそんなに難しい概念ではない。

10進数がひとつの位で9までしか表記できず、その次となると上の（左の）位に繰り上がるのは誰でも知っている。
つまり「08」「09」と来てその次は、上の位に繰り上がって「10」だ。

2進数と10進数の違いは、ひとつの位で表記できる最大値の違い。
10進数が9までOKだったのに対し、2進数は1まで。
つまり「00」「01」と来てその次は、上の位に繰り上がって「10」となる。
同様に60進数は59までなので「59分」の次は繰り上がって「1時」になる。

たとえば「256」って、10進数ならこういう意味。

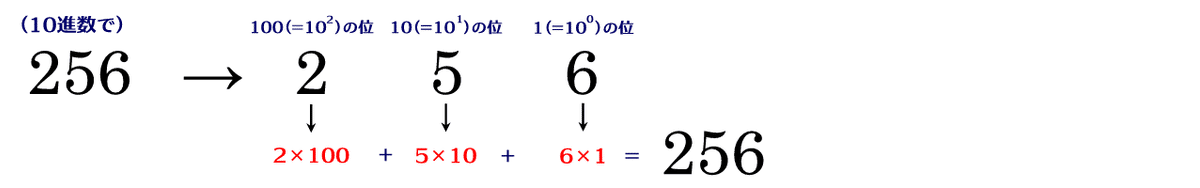
この3桁、左から100の位、10の位、1の位だから、$${(2\times100)+(5\times10)+(6\times1)=256}$$となるのだ。

10進数で「10101」は、同様に$${(1\times10000)+(0\times1000)+(1\times100)+(0\times10)+(1\times1)=10101}$$。

では同じ「10101」でも、2進数なら？
右から16の位、8の位、4の位、2の位、1の位だから、$${(1\times16)+(0\times8)+(1\times4)+(0\times2)+(1\times1)=21}$$となる。

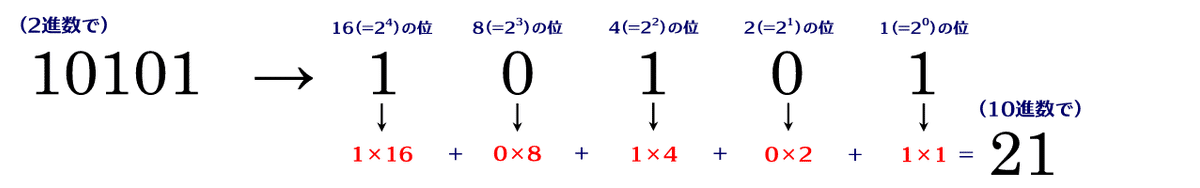
上の表で恐るおそる「10101」を見てみると、おぉ！「21」正解！

同じように計算すれば、5桁の2進数は最大「11111」、つまり$${(1\times16)+(1\times8)+(1\times4)+(1\times2)+(1\times1)=31}$$まで数えられる。
片手5本指で31まで数えたのは、2進数だったわけだ。

片手だと10までしか数えられない、いや5までだ…とお嘆きの方は、ぜひこの2進数を習得して31まで数えられるようになっておこう。
何の役に立つ？
そうだな、31までというと…日にちを数えるのに便利かも？

（2021/12/29記）