左確率行列の固有値問題

Introduction

左確率行列は、各列の要素の和が1になるような非負値正方行列のことです。例えばwebページの閲覧遷移を表現するために用いられています。この場合、i行j列の要素の値はページjからページiへのユーザーの遷移確率です。こうすることで、右から現時点で各ページが閲覧される確率を表すベクトルをかけることで、次の時点で各ページが閲覧される確率を求めることが出来ます。

さて、初期時点で各ページが等しい確率で閲覧されるとしましょう。

もし時点が進むにつれてページが閲覧される確率がある確率ベクトルに収束するのであれば、そのベクトルの各要素の値は各ページの重要度と思うことが出来るではないでしょうか。

このようなアイディアはGoogle PageRank algorithmなどに用いられています。

今回のテーマは、「特定の形をした左確率行列によって閲覧遷移が表現される場合には、このような確率ベクトルが存在する」ことを問題形式で触れ、証明することです。問題の出典は、東京大学大学院, 情報理工学系研究科, 数理情報学専攻の修士課程入試問題（平成30年8月実施）より専門科目第1問です。

問題

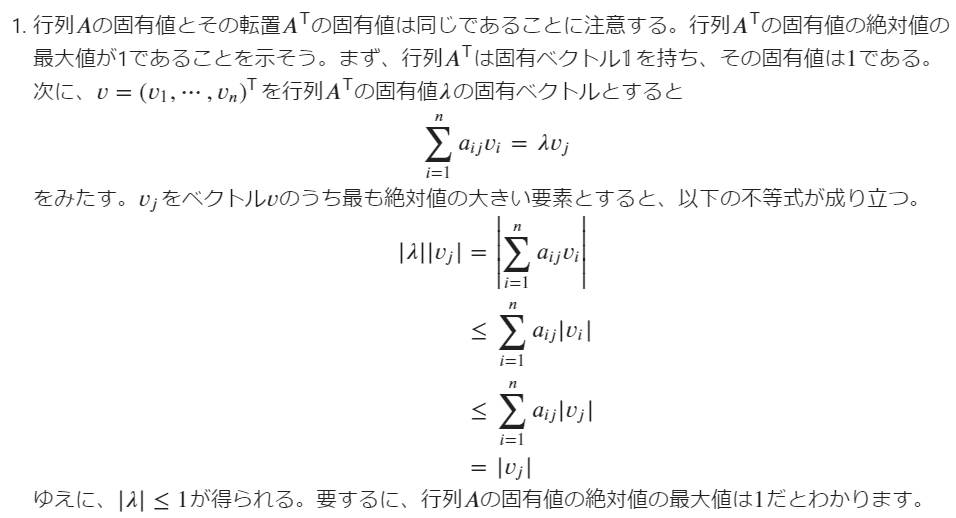
解答

Acknowledgement

すうがくぶんかの社内slackにて、梅崎先生から質問に答えて頂き、小問2で犯していた誤解（およびいくつかの誤字）を親切にご指摘頂きました。心よりお礼申し上げます。