
【勉強法】情報Ⅰ 大学入学共通テスト 試作問題 第4問データ分析解説 (大学入試センター 2022/11/9発表)
テクニック解説動画(第4問)
書籍出版します!
問題のダウンロード
問題の出典:大学入試センター
動画制作
文字おこし
大学入学共通テスト 情報Ⅰ 試作問題解説
今回は第4問のデータ分析に関する問題を解説していきます。
この第4問を解く上で四分位数と箱ひげ図および外れ値に関する事前知識が必要になりますので、先に数分以前の授業動画をご覧ください。
第4問 問1
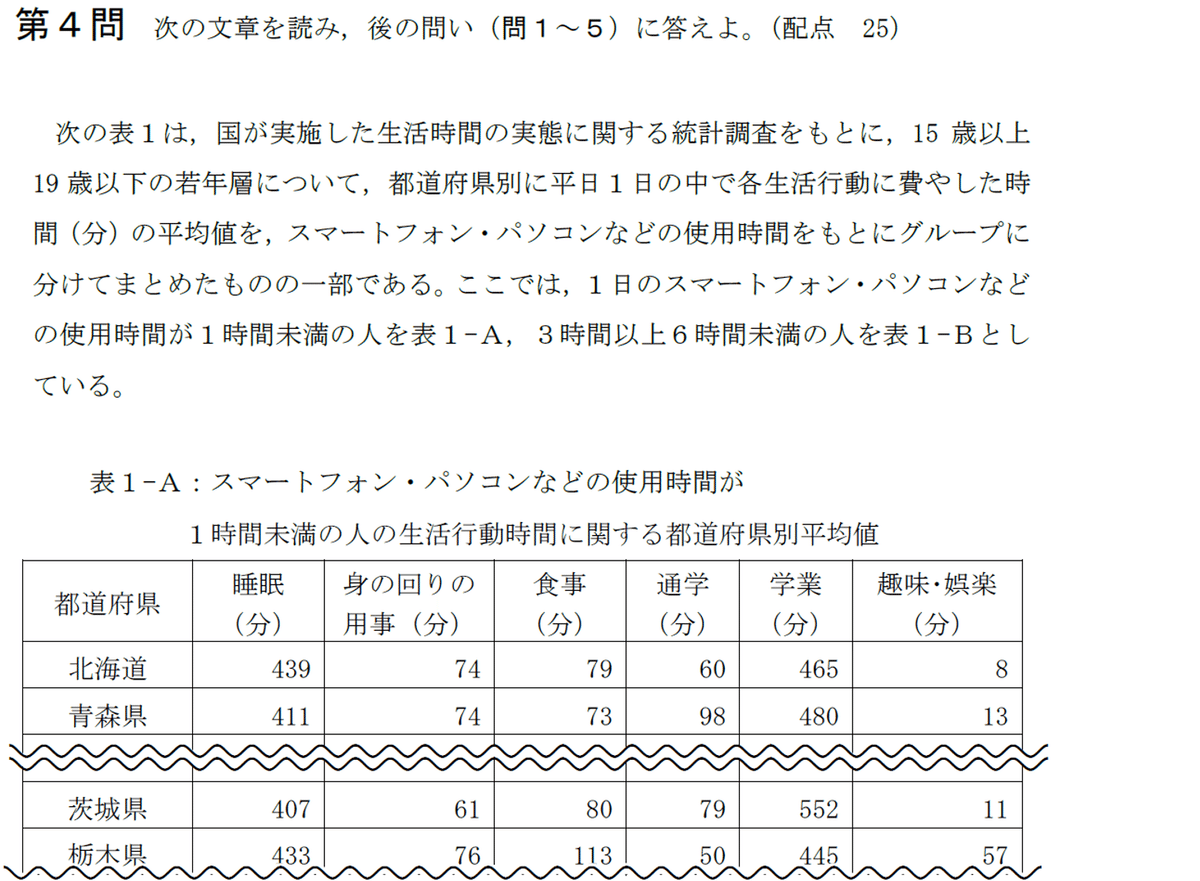

それでは問1から解説していきます。
「花子さんたちは,これらのデータから次のような仮説を考えた。表1-A,表1-Bのデータだけからは分析できない仮説を,次の⓪~③ のうちから一つ選べ。 」
選択肢を1つずつ見ていきます。

0番の「若年層でスマートフォン・パソコンなどの使用時間が長いグループは,使用時間が短いグループよりも食事の時間が短くなる傾向があるのではないか。」については、それぞれの表の食事時間を比較すれば分析できる仮説になります。

1番の「若年層でスマートフォン・パソコンなどの使用時間が長いグループに注目すると,スマートフォン・パソコンなどを朝よりも夜に長く使っている傾向があるのではないか。」については、スマートフォン・パソコンの使用時間が長い表1-Bに着目しても、朝と夜を明確に分ける項目がないので分析は出来ません。よって、1番が正解になります。
他の選択肢も見ていきます。

2番の「若年層でスマートフォン・パソコンなどの使用時間が長いグループに注目すると,学業の時間が長い都道府県は趣味・娯楽の時間が短くなる傾向があるのではないか。」については、それぞれの「学業」と「趣味・娯楽」の項目を比較すれば分析できる仮説になります。
※動画内の説明で一部誤りがありました(このブログは訂正済)

3番の「若年層でスマートフォン・パソコンなどの使用時間と通学の時間の長さは関係ないのではないか。」については、「通学」の項目を比較すれば分析できる仮説になります。
問2

次に問2の解説をしていきます。
先程冒頭で説明した、箱ひげ図の読取り問題になります。
「花子さんたちは表1-A,表1-Bのデータから睡眠の時間と学業の時間に注目し,それぞれを図1と図2の箱ひげ図(外れ値は〇で表記)にまとめた。これらから読み取ることができる最も適当なものを,後の 0~3 のうちから一つ選べ。」について順番に選択肢を確認していきます。

0番の「睡眠の時間が420分以上である都道府県の数をみたとき,表1-Aの方が表1-Bよりも多い。」については、図1の睡眠の時間の分布に着目すると420分は、この赤色点線あたりになります。
先程説明したように、箱ひげ図の箱の左側の線は第1四分位数なのでデータ全体個数の25%に位置する値になります。
表1-Aの第一四分位数の位置は、420分を超えていません。表1―Bの第一四分位数の位置は、420分を超えています。つまり、1-Aの方が420分を超えている都道府県が少ないということが分かります。よって、0番の選択肢は不正解になります。

1番の「学業の時間が550分以上の都道府県は,表1-Aにおいては全体の半数以上あり,表1-Bにおいては一つもない。」については、図2の学業時間の分布に着目します。
550分は、この赤色点線の線になります。
半分以上とあるので、箱の中にあるまん中の線の第2四分位数(中央値)に注目します。
表1―Aの第2四分位数の線が550分以上の領域に入っていないので、550分以上の都道府県は、半分以上とは言えません。
表1-Bについては、一番右の最大値が550分の領域に入っていないので、550分は1つもないと言えます。前半部分の1-Aの説明が誤っているので不正解となります。

2番の「学業の時間が450分未満の都道府県は,表1-Bにおいては全体の75%以上であり,表1-Aにおいては50%未満である。」については、図2の学業の時間の分布に着目します。
450分の線は赤色点線部分で分かりやすくするために領域を塗りつぶしておきます。
表1-Bについて、全体の75%は、第3四分位数なので箱の右側の線が対応しています。
第3四分位数の線が、450分未満領域に入っているので学業の時間が450分未満の都道府県は75%以上であると言えます。
後半文章について表1-Aの50%の位置にある第2四分位数の線に注目すると、450分未満の領域に入っていないので、450分未満の都道府県は50%未満であると言えます。
よって、2番が正解になります。

3番の「都道府県別の睡眠の時間と学業の時間を比較したとき,表1-Aと表1-Bの中央値の差の絶対値が大きいのは睡眠の時間の方である。」については、中央値の比較なので第2四分位数である箱の中の線の差になります。図2の方が範囲が広いので学業の方が差の絶対値が大きいので誤りになります。
―――――――――――
問3

次に問3の解説をしていきます。
「花子さんたちは,スマートフォン・パソコンなどの使用時間の長さの違いが,睡眠の時間と学業の時間のどちらに大きく影響しているかについて調べることにした。そのために,都道府県ごとに睡眠の時間と学業の時間のそれぞれにおいて,表1-Aの値から表1-Bの値を引いた差について考え,その結果を次の図3の箱ひげ図(外れ値は〇で表記)で表した。図3について述べたこととしてA~Eの中から正しいものはどれか。当てはまるものの組合せとして最も適当なものを,後の⓪ ~⑤ のうちから一つ選べ。」
選択肢を1つ1つ確認していきます。

Aの「学業の時間の差が正の値になっている都道府県の若年層は,スマートフォン・パソコンなどの使用時間が短いグループの方が,学業の時間が長い傾向にある。」については、これは箱ひげ図を見なくても解ける問題になります。例えば極端ですが、使用時間の短いグループAの学業時間を5分、使用時間の長いグループBの学業時間を2分とした場合、その差を求めて3分と正の値になるので、使用時間の短いグループAの方が学業時間が長いことになります。
つまり、Aは正しいです。

Bの「睡眠の時間の差が正の値になっている都道府県の若年層は,スマートフォン・パソコンなどの使用時間が短いグループの方が,睡眠の時間が短い傾向にある。」については、これもAと同じ考え方になります。
例えば極端ですが、使用時間の短いグループAの睡眠の時間を5分、使用時間の長いグループBの睡眠の時間を2分とした場合、その差を求めて3分と正の値になるので、使用時間の短いグループAの方が睡眠の時間が長いことになります。
つまり、差が正の場合「睡眠の時間が短い」というのは誤りになります。

Cの「スマートフォン・パソコンなどの使用時間による生活行動時間の差は,睡眠の時間よりも学業の時間の方に顕著に表れている。」については、それぞれの箱ひげ図の高さのことになります。
睡眠の時間よりも学業の時間の方の大きいつまり顕著に表れているので正解となります。
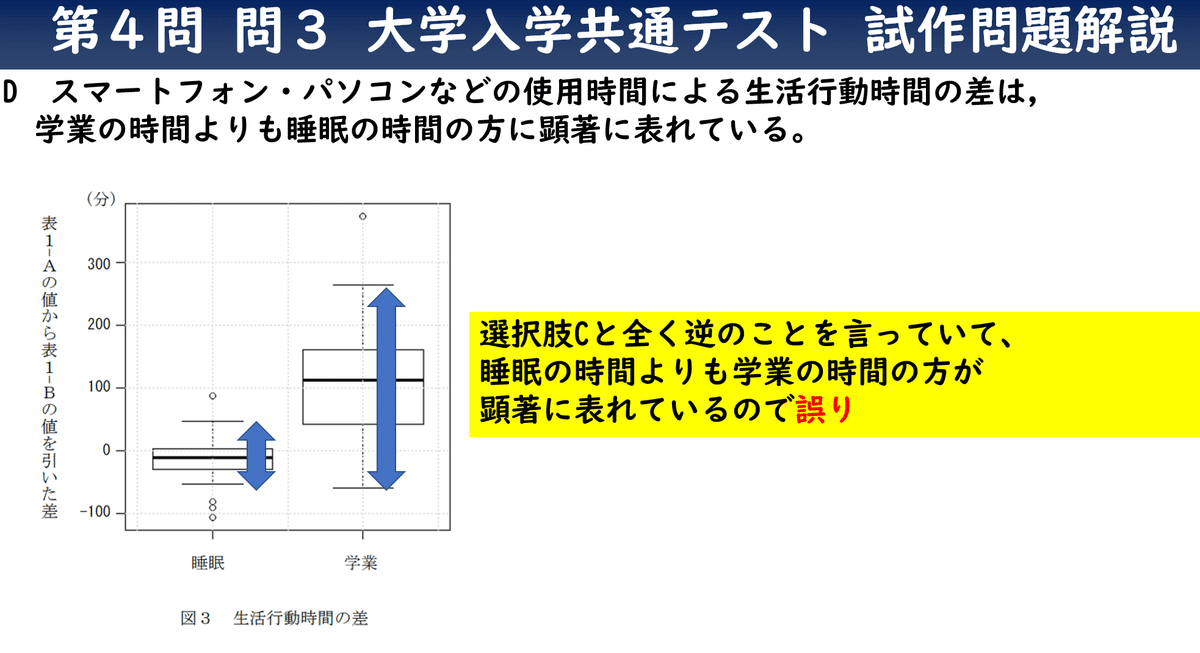
Dの「スマートフォン・パソコンなどの使用時間による生活行動時間の差は,学業の時間よりも睡眠の時間の方に顕著に表れている。」については、選択肢Cと全く逆のことを言っていて、睡眠の時間よりも学業の時間の方が顕著に表れているので誤りになります。

Eの「スマートフォン・パソコンなどの使用時間による生活行動時間の差は,学業の時間と睡眠の時間の両方に同程度に表れている。」については
先ほどの選択肢C、Dの話より同程度とは言えませんので、誤った選択肢になります。

よって、AとCが正なので0番が正解になります。
問4

次に、問4について見ていきます。
「花子さんたちは,表1-Aについて,睡眠の時間と学業の時間の関連を調べることとした。次の図4は,表1-Aについて学業の時間と睡眠の時間を散布図で表したものである。ただし,2個の点が重なって区別できない場合は □ で示している。」
都道府県単位でみたとき,学業の時間と睡眠の時間の間には,全体的には弱い負の相関があることが分かった。この場合の負の相関の解釈として最も適当なものを,次の ⓪~③ のうちから一つ選べ。なお,ここでは,データの範囲を散らばりの度合いとして考えることとする。
この問題については、図表からどの程度のばらつきや相関関係があるかの読取りが難しいです。問題文の中にある「学業の時間と睡眠の時間の間には,全体的には弱い負の相関があることが分かった」というのが大きなヒントとなります。
負の相関は、「一方が増加すると、もう一方は減少する傾向がある」というものです。
つまり、「学業の時間が増加すると、睡眠の時間が減少する」逆に「学業の時間が減少すると、睡眠の時間が増加する」という意味です。
このことから最も妥当な選択肢は2番の「学業の時間が長い都道府県ほど睡眠の時間が短くなる傾向がみられる」になります。
問5

次に問5を確認していきます。
「花子さんたちは都道府県別にみたときの睡眠の時間を学業の時間で説明する回帰直線を求め,図4の散布図にかき加えた(図5)。すると回帰直線から大きく離れている県が多いことが分かったため,自分たちの住むP県がどの程度外れているのかを調べようと考え,実際の睡眠の時間から回帰直線により推定される睡眠の時間を引いた差(残差)の程度を考えることとした。そのために,残差を比較しやすいように,回帰直線の式をもとに学業の時間から推定される睡眠の時間(推定値)を横軸に,残差を平均値0,標準偏差1に変換した値(変換値)を縦軸にしてグラフ図6を作成した。参考にQ県がそれぞれの図でどこに配置されているかを示している。また,図5の □ で示した点については,問題の都合上黒丸で示している。」

空欄オの部分から図と突き合わせて確認していきます。空欄オは、外れ値となる都道府県の数が問われてています。
ヒントとしては、「平均値から標準偏差の2 倍以上離れた値を外れ値とする基準」とあります。
また、「図5の残差を平均値0,標準偏差1に変換した値(変換値)を縦軸にしてグラフ図6を作成した。」とあります。
つまり、「平均値0から標準偏差の1の2倍である、2以上離れているものが外れ値」と言い換えられます。平均値から2以上離れている領域は、ピンク色の網掛け部分で、0と2が該当するので2個になります。

次の空欄カは図5中のP県について、図6の0~3どれが対応しているかが問われています。
ヒントとして既にそれぞれの図で明示されている。Q県の場合、回帰直線の睡眠の時間が406.8 、残差は正の値でこの青色矢印の様な対応関係があります。
P県を見てみると、回帰直線の睡眠の時間は約430分、残差は赤色下矢印の部分となり、残差は負の値であることが分かります。
図6で置き換えると、睡眠の時間430前後のゾーンで残差が負であるものは1番だけが該当するので答えは1番になります。
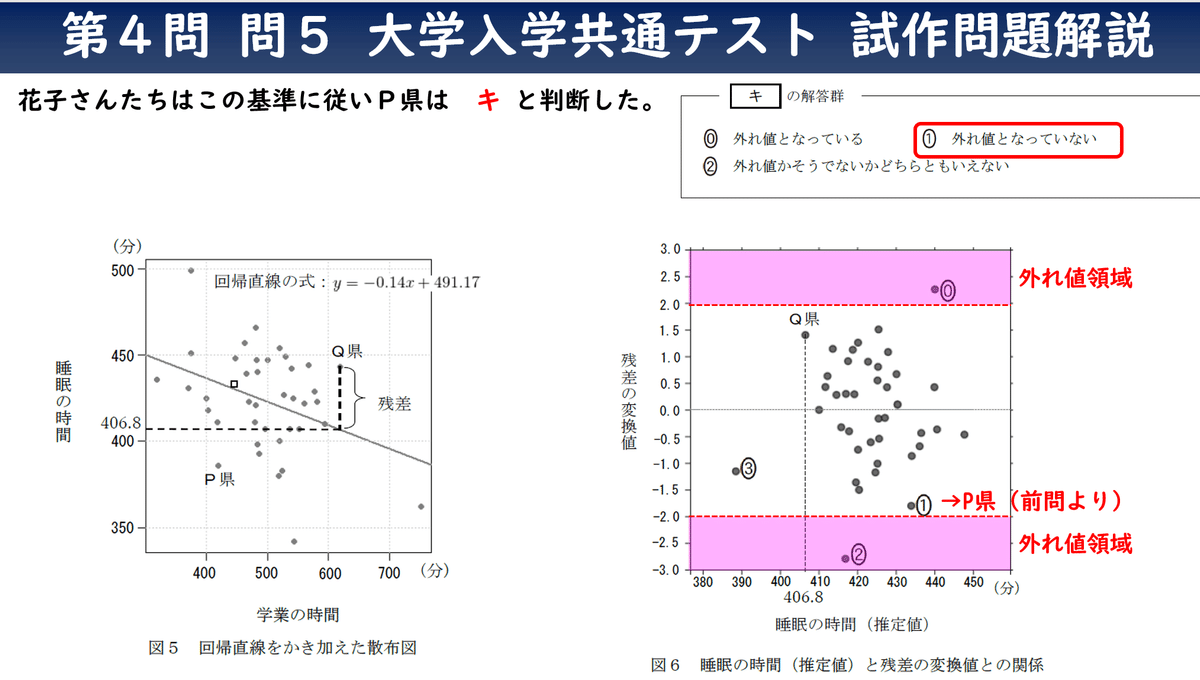
空欄キはP県の外れ値への近さが問われています。
今までの問を理解していないと解けない問題になります。
図6より先程の空欄キの答えよりP県は1番の位置に該当し、外れ値は2以上、―2以下のゾーンが該当します。つまり、―2のゾーンに入っていないので①の「外れ値となっていない」が正解になります。
情報科の先生へ(入試過去問・オリジナル問題など情報共有サイト)
実は、この共通テスト試作問題 情報Ⅰ 第4問で使用されている元データはオープンデータ提供サイトのe-Statから実際にダウンロードすることが可能です。
何と元のデータは34万行以上データ行があります。
それがExcelなど分析ツールを使うことで、このようなシンプルな形で分析できます。
https://t.co/VrAWMjQz7F
そしてなんと、情報科教諭のMatsushima先生が、この試験問題をエクセルでシミュレーションして再現してくれました。
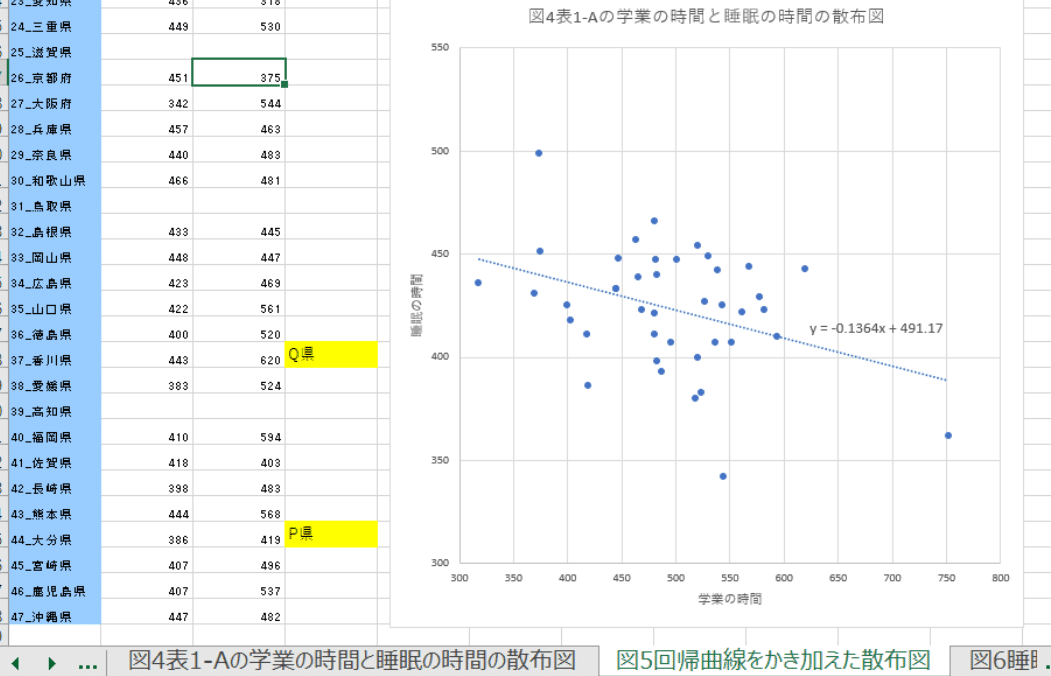
試験で問われているP県がありますが、なんと実際は私の故郷の大分県の様です。
Matsushima先生は、私が大変尊敬している情報科の先生ですが、現在の共通テスト科目「情報関係基礎」などの解説サイトを独自に構築され、情報処理学会の電子図書館などでも、その内容が公開されています。
情報科の先生は、授業単位数の関係で、ほとんどの学校では 1 校に 1 人 多くても2人しか配置されていません。
2025年の共通テストから情報Ⅰは共通テストの入試科目になります。情報Ⅰは2単位、つまり、最大でも70コマしかない中で、特に進学校の先生は入試に対して結果を出すことも求められてくる可能性もあります。しかし、1 人で相談できる相手もおらず,入試に入ることでさらに不安になっている情報科の先生も多いと思います。
【教科「情報」問題データベース】
そんな中、最近Matsushima先生は、情報科の先生、または情報科の先生を目指す学生向けに、学校で扱ったオリジナルの定期試験の問題、すでに情報入試を行っている大学の過去問題などお互いに情報交換できるサイトを立ちあげてくださいました。
Matsushima先生が提供されているサイトのリンクを概要欄に貼っていますので、是非 情報科の先生は登録して、お互いの情報を交換して頂けると嬉しいです。
https://note.com/tkmium/n/nc2ca7ce40273
第4問の解説は以上になります。
最後までご視聴ありがとうございました。
