ストロークのコースとショット到達時間
こんにちは、トモヒトです。
今回は、ストロークのコースが、ショット到達時間にどのような影響を及ぼすかを考えてみます。
検証方法
今回は、プログラムを用いて、ショット到達時間を算出していきます。
条件は、次のようになります。
定数(物理定数、用具)
重力加速度=9.81m/s^2
空気密度=1.21kg/m^3
反発係数=0.75
摩擦係数=0.72
ボール半径=0.033m
ボールの質量=0.0577kg
変数
球速:90km/h~160km/hの範囲で5km/h刻み
ショットの打ち出し角度:1~19.8度の範囲で0.2度刻み
回転量:900~2550回転の範囲で50回転刻み
座標:アドサイドのシングルスサイドラインとベースラインの交点を、(0, 0)として、xに関してはデュースサイド方向を正、yに関してはネット方向を正とする
打点の高さ=1m

ショット到達時間に関しては、ベースライン後方2mのラインを越えるか、2バウンドしたときの時間とし、球速ごとに最短の到達時間を算出します。
ショットの軌道を求める式は、以下のサイトを参考にし、次のように設定しました。
$$
v=ショット速度 w=spin ×\frac{\pi}{30} spin=回転量\\
抗力係数\\
Cd = 0.508 × \frac{1}{22.503 +4.196((\frac{v}{0.033×w})^{2.5})^{0.4}} \\
揚力係数\\
Cl = \frac{1}{2.02+0.981(\frac{v}{0.033×w})} \\
水平方向の加速度\\
\frac{0.033^2×\pi×1.21×v}{2×0.0577}(-Cd×v_x + Cl×v_y)\\
垂直方向の加速度\\
\frac{0.033^2×\pi×1.21×v}{2×0.0577}(-Cd×v_y - Cl×v_x) - 9.81
$$
水平方向・垂直方向の加速度の式を、連立微分方程式として解いてボールの軌道を求めます。
これらの処理を行うコードは、以下になります。
import pandas as pd
import numpy as np
def search_shot(sv, shot_angle, spin, net_height, shot_distance):
ball_radius = 0.033 # ボールの半径 (メートル)
A = np.pi * (ball_radius**2) # ボールの断面積 (m^2)
m = 0.0577 # ボールの質量 (kg)
shot_v = sv / 3.6
w = spin * (np.pi / 30)
net_length = shot_distance[0]
net_height += ball_radius
shot_length = shot_distance[1]
bound_length = shot_distance[2]
hitting_point_distance = shot_length + bound_length
# 物理定数
g = 9.81 # 重力加速度 (m/s^2)
rho = 1.21 # 空気密度 (kg/m^3)
e = 0.75 # 反発係数
myu = 0.72 # 摩擦係数
v0 = np.zeros(4)
v0[1] = 1 # 打点の高さ (m)
v0[2] = shot_v * math.cos(math.radians(shot_angle))
v0[3] = shot_v * math.sin(math.radians(shot_angle))
t_min = 0
t_max = 5
dt = 0.001
t = np.arange(t_min, t_max, dt)
t_span = (t_min,t_max)
solved_data = solve_ivp(f, t_span, v0, t_eval=t, args=(ball_radius, w, rho, m, g, A))
flag = True
for i in range(len(solved_data.t)):
if solved_data.y[0, i] >= net_length - 0.02 and solved_data.y[0, i] <= net_length + 0.02 and solved_data.y[1, i] <= net_height:
return np.nan, np.nan, np.nan
if solved_data.y[1, i] <= ball_radius:
if solved_data.y[0, i] <= net_length:
return np.nan, np.nan, np.nan
elif solved_data.y[0, i] <= shot_length:
shot_time = solved_data.t[i]
reach_time = solved_data.t[i]
y2 = np.zeros(4)
y2[0] = solved_data.y[0, i]
y2[1] = solved_data.y[1, i]
y2[2] = solved_data.y[2, i] * e - myu * g
y2[3] = - solved_data.y[3, i] * e
if solved_data.y[2, i] - w > 0:
w = w - myu * g
elif solved_data.y[2, i] - w < 0:
w = w + myu * g
break
else:
return np.nan, np.nan, np.nan
solved_data = solve_ivp(f, t_span, y2, t_eval=t, args=(ball_radius, w, rho, m, g, A))
flag = False
for i in range(len(solved_data.t)):
if len(solved_data.t) == i - 1:
break
if solved_data.y[1, i+1] - solved_data.y[1, i]:
flag = True
if solved_data.y[0, i] >= hitting_point_distance or (flag and solved_data.y[1, i] <= ball_radius):
bound_time = solved_data.t[i] + 0.004
reach_time += solved_data.t[i] + 0.004
return shot_time, bound_time, reach_time
def f(t, y, ball_radius, w, rho, m, g, A):
u, udot = y[:2], y[2:]
v = np.sqrt(udot[0]**2 + udot[1]**2)
# 抗力係数
Cd = 0.508 + (1 / ((22.503 + 4.196 * (v / (ball_radius * w)) ** 2.5) ** 0.4) )
# 揚力係数
Cl = 1 / (2.02 + 0.981 * (v / (ball_radius * w)))
udotdot_x = ((A * rho * v) / (2 * m)) * (- Cd * udot[0] + Cl * udot[1])
udotdot_y = ((A * rho * v) / (2 * m)) * (- Cd * udot[1] - Cl * udot[0]) - g
dydt = np.hstack([udot, udotdot_x, udotdot_y])
return dydtimport itertools
columns = ["shot velocity", "shot angle", "spin rate"]
df = pd.DataFrame(columns=columns)
v = [x for x in range(90, 165, 5)]
a = [x for x in np.arange(1, 20, 0.2)]
s = [x for x in range(900, 2600, 50)]
for i, comb in enumerate(itertools.product(v, a, s)):
df.loc[i, columns] = list(comb)
x = 0 "左右の位置"
y = 0 "前後の位置"
for i, l in enumerate([23.77/2+6.4, 23.77/2+6.4+((23.77/2-6.4)/2), 23.77]):
print(l)
# Near Side
if x == 0:
bound_l = l - y
net_l = 23.77/2 - y
shot_l = 23.77 - y + 2
net_height = 1.042
else:
bound_l = np.sqrt((l - y) ** 2 + x ** 2)
net_l = bound_l * (((23.77/2) - y) / (l - y))
shot_l = bound_l * ((23.77 - y + 2) / (l - y))
net_height = min(1.07, 0.914 + (0.156 * (((8.23 / 2) - x + (np.sqrt((net_l ** 2 - ((23.77/2) - y) ** 2)))) / 5.029)))
result_columns = [f"shot time near{i}", f"bound time near{i}", f"reach time near{i}"]
df[result_columns] = df[columns].apply(
lambda x: search_shot(x[0], x[1], x[2], net_height, [net_l, bound_l, (shot_l - bound_l)]),
axis=1,
result_type="expand"
)
# Far Side
bound_l = np.sqrt((l - y) ** 2 + (8.23 - x) ** 2)
net_l = bound_l * (((23.77/2) - y) / (l - y))
shot_l = bound_l * ((23.77 - y + 2) / (l - y))
net_height = min(1.07, 0.914 + (0.156 * (abs(((np.sqrt((net_l ** 2 - ((23.77 / 2) - y) ** 2) + x)) - (8.23 / 2))) / 5.029)))
print(bound_l, net_l, shot_l, net_height)
result_columns = [f"shot time far{i}", f"bound time far{i}", f"reach time far{i}"]
df[result_columns] = df[columns].apply(
lambda x: search_shot(x[0], x[1], x[2], net_height, [net_l, bound_l, (shot_l - bound_l)]),
axis=1,
result_type="expand"
)
結果
シングルスサイドラインから
まずは、x=0, y=0のときのコース別のショット到達時間を見てみます。
これは、シングルスサイドラインとベースラインの交点にあたります。
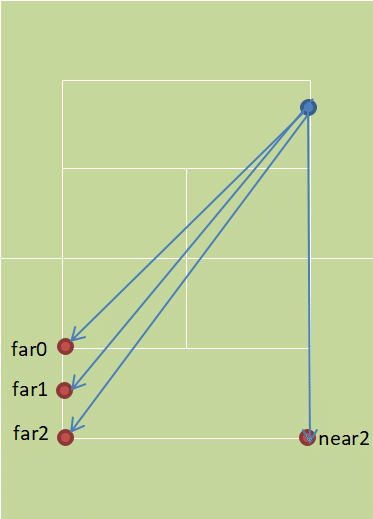
near2:ストレート方向のベースライン
far0:クロス方向のサービスライン
far1:クロス方向のサービスラインとベースラインの中間
far2:クロス方向のベースライン
対象のショットのイメージは、以下の図に表しています。

コースごとのショット到達時間は、下の表のとおりです。
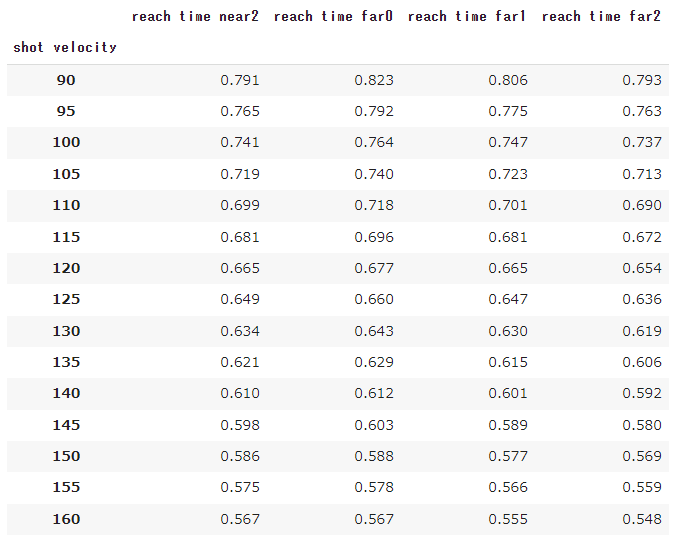
ショット到達時間をみると、コース間で大きな差がないことがわかります。
near2を1としたときのクロス方向のショットの到達時間との比は次のようになります。

シングルスサイドライン・コート内のポジション
まずは、x=0, y=1のときのコース別のショット到達時間を見てみます。
これは、先ほどのポジションから1mコート内に入ったポジションにあたります。

シングルスサイドラインとベースラインの交点のポジション時と同様、コース間で大きな差がないことがわかります。

センター寄りのポジションから
次は、x=3, y=0のときのコース別のショット到達時間を見てみます。
シングルスコートの半面の横幅は4.115mほどなので、これはセンターから約1m外側のポジションになります。


ポジションがセンター寄りとなっても、コース間で大きな差がないことがわかります。

考察
今回は、3ポジションからのコース間でのショット到達時間の差を見てきました。
コース間で比較すると、ほとんど差が見られないという結果でした。
ストレートとクロスでの差をみると、0.01秒前後、多くても0.02秒前後となっており、プレーヤーが20km/h(5.56m/s)で走るとすると、0.01秒は5cmの違いとなっています。
この結果から考えると、ショットの返球可能範囲の二等分線に構える「合理的待機位置」は妥当だと考えられます。
ただし、今回はショットの球速を一定値に固定した状態で、回転量とショットの打ち出し角度を変化させて、各コースで最短の到達時間を割り出している点に、注意が必要です。
仮に、プレーヤーがコースごとにショットの球速を変えていれば、今回の結果をそのまま当てはめることができません。
あくまでも、物理学的な検証であり、今後現実との比較を行う必要があると考えられます。
まとめ
今回は、コース別のショット到達時間を物理的に算出して比較しました。
コースごとに到達時間を把握する試みは、テニスの戦術を考えるうえでもカギになると考えています。
物理的にショットの到達時間を算出する方法論と、実際のデータを組み合わせることで、戦術の考察が深まるのでは?と感じます。
最後までお読みいただきありがとうございました。
ご意見ご感想あれば、コメントにお願いします。
この記事が気に入ったらサポートをしてみませんか?
