【動画あり】第7回問い立てスクール「教科横断型授業」~俳句・短歌・川柳をよもう~
オープニング ~教科横断型授業とは~
問い立てラボ代表の山﨑の持論だが,学校の授業に大きく足りないものがあります。それは学んだことを使う場面です。経済産業省の未来の教室ではこのような図を使っています。
第17回問い立てラボで浅野大介氏が言われていたのは,経産省では「創る⇄知る」の授業が「主体的・対話的・深い学び」になる。つまり,教科横断型授業をしたいのではないくて,知れば創りたくなる,創ろうとすれば知りたくなる,「創る⇄知る」のワクワクする授業をしたいのです。この「創る⇄知る」の授業をすれば,必然的に教科を横断してしまうのだと思います。
(動画は記事の最後にあります)
1時間目:国語(15分)~短歌,俳句は「すごい,芸術だ」ではない!!
子供たちがポケモンの名前をいえる,カープファンが背番号で選手が分かる,平安人にとっても歌をつくることは,本人たちにとってはすごいことではない。
感動したら歌にしていた。そう,それは現代の・・・
短歌・俳句を作るコツ
どちらがみなさんにとっていい感じですか?
みなさん,満場一致で「b」でした。さてなぜでしょう??それは,「アイス」と「こたつ」の組み合わせがポイントなんです。
二つ組み合わせるといい感じになる。
↑うえの赤字が「とりあわせ(二句一章)」という俳句の技の例である。
「見えているもの(鐘)」と「場所(上野・浅草)」,「匂うもの(味噌豆)と見えるもの(おぼろ月)と,聞こえるもの(けいこ笛)と見えるもの(田)」と思った人もいるかもしれませんが,それでもOKです。こうすることで俳句がいい感じに聞こえるそうです。
不思議ですね,なんででしょうね。日本語がわかる海外の人も「いい感じに」聞こえるんですかね?(山﨑の独り語)
とりあわせ(二句一章)がない,一物仕立てもあるが,一物仕立ての方が難易度は高いらしい。
俳句といえば・・・
あ,これは「バイク」でしたね(笑)
俳句といえば・・・十六茶ではなく「おおいお茶」
以下,多いお茶の俳句の大賞作品の紹介です。
「猫」と「ヘルスメーター」がとりあわせになってますよね。情景が浮かびますよね。
駅を出て街のかけらとなっていく(高校生の作品)
十五夜に飛ぶ蝙蝠よまぶしいか(中学生の作品)
たんぽぽがおそれを知らずに旅に出る(小学生の作品)
2時間目 理科(15分)科学の目で見る情景分析
理科も俳句も「観察」だ!!では昔の歌を詠んだ人は,どのように観察していたのか?
みなさんは,↓↓どんな風景が浮かびますか?
日が沈んで,月が東に見えるから夕暮かな??
理科的に考察すると,↓↓下の図の3人いる中で,「下の人」の立ち位置になる。つまり,満月で夕方ということが分かる。
恐竜の肌が虹色ってどういうこと??
次にこの歌はどんなことが分かりますか?↓↓
実は,恐竜って,骨格はわかるけど,色は分からないらしい。もしかしたら虹色の恐竜がいたのかも?
さらに,恐竜は色も分からなければ,羽毛が生えていたかどうかも分かっていない。素風(秋にふくそよ風のこと)が吹くことで,生えてたかもしれない羽毛がなびく情景を歌にしたようです。恐竜の不思議や科学のこれからの期待を表した歌のようです。
銃弾を惑星の地面に打ち込んで,浮き立った砂をキャッチして持って帰った「はやぶさ」を,「ホウセンカ」の種のようだと歌った歌。「はやぶさ」と「ホウセンカ」が「とりあわせ(二句一章)」にもみえます。
これは,講師の花ノ木先生が読んだ歌です。
日の出,月の出はいうけど,「地球の出」が出てきた情景を,「荒涼」で寒々しい月の表面を表し,「宙をのぼりし」で宇宙を走っている様子,「生命の青」で,月から見る青々とした地球をみた感動を表している。まさに感動したら歌を詠む,そんな気持ちで作ったようです。
3時間目 数学(15分)フィボナッチ数列と5・7・5
ふと疑問に思うのです,なぜ5・7・5なのか?5・7・5じゃなくてもいいんじゃないの??それを数学的に読み解いていきます。
次に入る数字は何か分かりますか?↓
正解は,↓
フィボナッチ数列と「黄金比」
では,これは分かりますか?これがフィボナッチ数列です。↓↓
正解は「8」です。二つ前と一つ前を足したら次の数になる数列,これをフィボナッチ数列といいます。そして,このフィボナッチ数列の数が増えていけばいくほど,隣どうしの数がある比率になります。そのある比率こそが,「黄金比(1:(1+√5)÷2)」です。黄金比は紀元前から使われており,西欧では見た目が美しく見えるとされ,建物,芸術作品などにも多く疲れています。
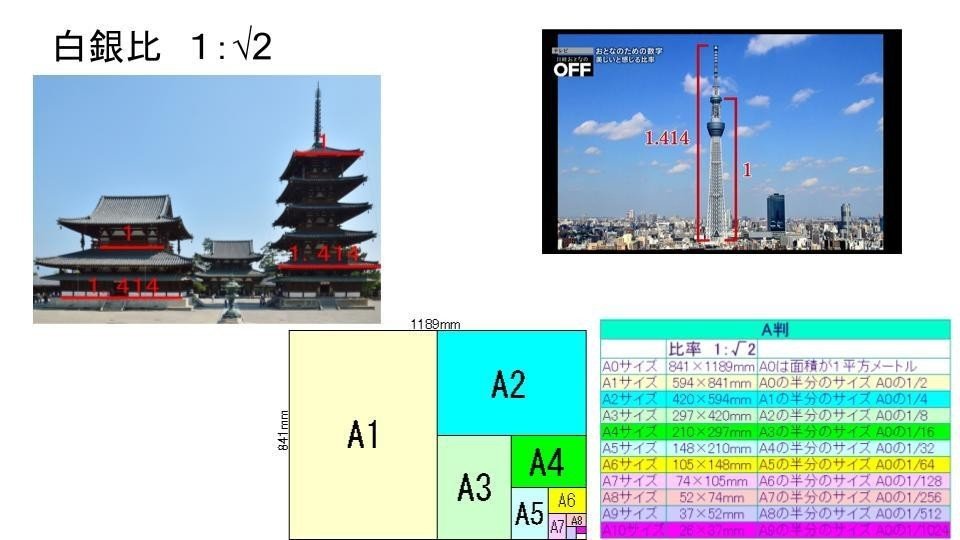
日本人好みの「白銀比」
日本人には黄金比よりも「白銀比(1:√2)」がなじみやすく,美しいとされて日本の建造物,キャラクターなどにも多く使用されています。
ちなみに,黄金比は「正五角形の辺と対角線」の比率で,白銀比は「正方形の辺と対角線」の比率です。
もしかして「正六角形の辺と対角線」の比率も美しいのかな??(山﨑の独り言)
私(数学)の仮説
日本人が5・7・5が好きなのは,「白銀比」が整数で「約5:7」だからなのではないか。だったら,「黄金比」の整数比「約5:8」あるいはフィボナッチ数列の数「3,5,8,13…」で作っても美しく聞こえるのはないか。(なぜなら,フィボナッチ数列の隣どうしの比率は「黄金比」だから)
ここで私も一句,なんか3,5,8でもきれいに聞こえませんか↓↓?
ちなみに,理科の目線でいうと,蚊がとまるのは子供の方が体温が高いからではないかと,花ノ木先生は言う。なるほど,私にはそういう目線はなかった。
最後に,教科横断型授業とは
俳句って本当に国語の教科なんでしょうか?理科の見方考え方を使えば,はやぶさがホウセンカにもみえるし,数学の見方考え方を使えば,3・5・8でも美しくなる可能性がある。もはや俳句はどの教科でもあるのではないか,それが教科横断型授業なのではないか。私がオープニングで行った「創ろうとすれば知りたくなる,知れば創りたくなる」そんな教科の授業を学校で実践できれば,きっとワクワクする授業になるのではないか,その一例としてこの実践をみてもらえれば幸いです。
いいなと思ったら応援しよう!