
【解説】情報関係基礎 平成31年度 センター試験 2019

第1問(必答)
問1
a
ア : ⑨暗号化
イ : ⓪Webサーバ
ウ : ④ファイル名
エ : ①国名
オ : ②大学や企業のような組織種別
カ : ⓪DNSサーバ
H30年でも似た問題が出題されていましたね。

HTTP(Hyper Text Transfer Protocol)とは、サーバとクライアント間でデータをやり取りする際に使うプロトコル(通信規約)です。
HTTPSとは、Hyper Text Transfer Protocol 「Secure」のことで、HTTPの通信をセキュア(暗号化して)やり取りするよというものです。(なので、https自体は厳密にはプロトコルではありません。)
HTTPSではSSL(Secure Socket Layer)/TLS(Transport Layer Security)というプロトコルが使われています。SSLがSSL3.0バージョンアップを重ねた後、TLS1.0に名称変更されたのでいまだにSSLと言われたり、SSL/TLSと併記されたりしています。
近年世界的にSSL/TLS通信化が進んでいます。
2018年7月からGoogle Chrome(webブラウザ)で、httpsではないサイトで「保護されていない通信」と表示されるようになりました。
トップレベルの.jpなどが国名、第2レベルが組織などです。
DNS(Domain Name System)等は基本中の基本ですね。
b
キ : ③パケット
クケコ : 255
サ : ④28
32ビットIPアドレスは8ビットずつ区切って表示します。
28は256なので、0から開始すると255まで表示できます。
ビット数を32から40に増やすと232から240に増えるので表示できるIPアドレスの個数は28倍になります。
c
シ : ④復号
ス : ③受信者の公開鍵
暗号化と復号の問題です。
選択肢の量子化や標本化などは暗号化するときの言葉ですね。
H30でも第1問の問2で出題されていました。
問2
セ : ⓪
ソ : ⓪
タ : ①
チ : ①
ツ : ②
テ : ③Aの状態が1かつCの状態が1
ト : ①SW1・SW2・SW2・SW1
セ~ツ
地道に当てはめて解いていきます。(かなり面倒だなと思いました…)
まず回路1の時を考えます。

全ての状態の時の出力の様子を表にしました。

回路2の時は、

以下のようになります。

テ
Bが1の時だけ抜き出すと、次の表のようになります。

XOR回路ですね。
ト
⓪のSW1・SW2・SW2・SW1 を表にしてみました。これが正解ですね。

XOR回路であればOKです。
この問題は問題文にヒントがありますね。
「テ : ③Aの状態が1かつCの状態が1」の時の出力2が、AとCの論理和の結果と異なることがわかった」
この文章です。
SW1・SW2・SW1にSW2が追加されてもXORであることには変わりないのです。
そもそも、SW2は0でも1でも回路は交差しているだけでどちらも繋がっています。
SW2が追加されても出力結果が逆になるだけなので問題ありません。今回は階を一つ増やしたので、SW2が一つ増えている①が正解でしたが、SW2が2つであれば正解です。
なので、SW1・SW2・SW1・SW2などでも正解です。
階をどれだけ増やしても今後はSW2を追加していけば良いというわけですね。
第2問(必答)
情報というより数学みたいな問題でした。
問題文をきちんと読んでいけば解答できます。
問1
アイ : 40
ウエ : 50
オ : ⓪a×s+p
カ : ④b×t+q
キ : ②a×(s+p)
ク : ⑥b×(t+q)
ケ : ③-t
コ : ⓪s
サ : ⑦h
シ : ⑥w
ア~エ
描画したい長方形は以下
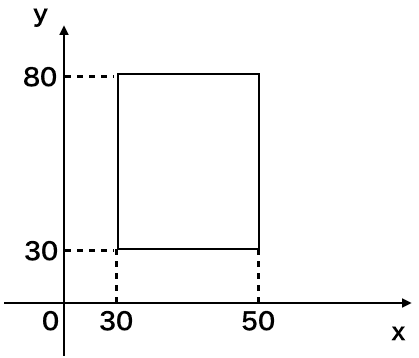
幅が20、高さが50です。また、中心点は((30+50)/2, (30+80)/2)で(40, 55)です。
よって、命令は 長方形(20, 55, 20, 50)となります。
オ~ク
原点中心倍率(a, b)は4つの頂点それぞれのx座標をa倍、y座標をb倍するので
中心(s, t)は(a×s, b×t)となり、幅と高さもそれぞれa倍、b倍されるので
長方形(s, t, w, h)→原点中心倍率(a,b)を実行すると
長方形(a×s, b×t, a×w, b×h)となります。
その後、移動(p, q)をするので中心の座標がx軸方向にp、y軸方向にq移動します。
よって、長方形(s, t, w, h)→原点中心倍率(a,b)→移動(p, q)を実行すると
長方形(a×s+p, b×t+q, a×w, b×h)となります。
また、移動(p, q)を先に実行すると、
長方形(s+p, t+q, w, h)を原点中心倍率(a,b)することになります。
よって長方形(a×(s+p), b×(t+q), a×w, b×h)となります。
ケ~シ
原点中心回転(Θ)は、長方形を回転移動するとあります。
図にすると以下のようになります。

注意するところは、中心(s, t)が中心(-t, s)となるところでしょうか。
幅と高さが入れ替わるところにも注意が必要です。
よって、長方形(s, t, w, h)→原点中心回転(Θ)は長方形(-t, s, h, w)となります。
問2
ス : ②-s
セ : ③-t
ソ : ⓪Θ
タ : ⓪s
チ : ①t
ツ : ⓪a
テ : ①b
トナ : 10
ニヌ : 70
ネノ : 40
ハヒ : 60
ス~テ
問題文通りに進めていきます。
(1)長方形の中心が原点になるように移動命令を用いる。
(2)原点中心回転命令を用いて回転移動する、または、原点中心倍率命令を用いて大きさを変える(3)長方形の中心が元の位置になるように移動命令を用いる
これを図にすると以下のようになります。

一旦原点に戻して、回転したりサイズを変更したりして、元の位置に戻すということですね。
<長方形(s, t, w, h)→長方形中心回転(Θ)>
長方形(s, t, w, h)を原点に移動したいので、移動(-s, -t)を行います。
これで長方形(0, 0, w, h)となります。
次に回転させるので、原点中心回転(Θ)を行います。
これで長方形(0, 0, h, w)となります。
元の位置に戻したいので、移動(s, t)を行います。
これで長方形(s, t, h, w)となります。
<長方形(s, t, w, h)→長方形中心倍率(a, b)>
長方形(s, t, w, h)を原点に移動したいので、移動(-s, -t)を行います。
これで長方形(0, 0, w, h)となります。
x軸にa倍、y軸にb倍したいので、原点中心倍率(a, b)を行います。
これで長方形(0, 0, a×w, b×h)となります。
最後に元の位置に戻したいので移動(s, t)を行います。
これで、長方形(s, t, a×w, b×h)となります。
ト~ヒ
命令文①
長方形(60, 20, 40, 20)→長方形中心回転(90)を行うと
長方形(60, 20, 20, 40)となります。
長方形(50, 30, 20, 40)と一致するためには、x軸方向に-10、y軸方向に+10移動する必要があるので
長方形(60, 20, 40, 20)→長方形中心回転(90)→移動(-10, 10)となります。
命令文②
長方形(60, 20, 40, 20)→原点中心回転(90)を行うと
長方形(-20, 60, 20, 40)となります。
長方形(50, 30, 20, 40)と一致するためには、x軸方向に+70、y軸方向に-30移動する必要があるので
長方形(60, 20, 40, 20)→原点中心回転(90)→移動(70, -30)となります。
命令文③
長方形(?, 10, 40, 20)→長方形中心倍率(0.5, 2)を行うと
長方形(?, 10, 20, 40)となります。
その後、移動(10, 20)を行なっているため長方形(?+10, 30, 20, 40)となります。
長方形(50, 30, 20, 40)と一致するので
(?+10)=50
?=40となります。
よって長方形(40, 10, 40, 20)→長方形中心倍率(0.5, 2)→移動(10, 20)となります。
命令文④
長方形(?, 25, 40, 20)→原点中心倍率(0.5, 2)を行うと
長方形(0.5×?, 2×25, 0.5×40, 2×20)すなわち長方形(0.5×?, 50, 20, 40)となります。
その後、移動(20, -20)を行なっているため長方形((0.5×?)+20, 30, 20, 40)となります。
長方形(50, 30, 20, 40)と一致するので
(0.5×?)+20=50
?=60となります。
よって長方形(60, 25, 40, 20)→原点中心倍率(0.5, 2)→移動(20, -20)となります。
第3問(選択)
問1
ア : 2
イ : 3
ウ : ③D
エ : ⑧I
オ : 4
カ : ⓪春
キ : ②秋
ク : ⑥G
アイ
クラスの生徒数が4の倍数でない場合には、生徒数を4で割った時の余りと同じ数のグループに生徒を1名多く振り分ける。
とあります。今回クラスの生徒数は10名なので
10÷4=2あまり2
より、2グループの人数が1人多いことになります。
よって2人のグループが2つ、3人のグループが2つできます。
ウエオ
図にしてみました。
方法1では、1名多いグループが先に決まるので、春・夏が3人のグループ、秋・冬が2人のグループとなります。

カキク
方法2では、第一希望の多いグループに振り分けるとあるので、春・秋が3人、夏・冬が2人のグループとなります。

よってGが方法1と違うグループになります。
問2
変数や配列が多すぎて頭が混乱してきますね。どこで何をしているのかをしっかり判断できないと少し難しい問題でした。問3も同様です。
第3問のプログラムは、for文やif文ごとに区切って考えるのがいいでしょう。
今回の問題だと以下のようになります。

トレースしながら合うものを見つけるのがおすすめです。
本番では途中までのトレースで構いませんが、勉強のときは全てやってみるといいです。
今回のプログラムをトレースしたものを以下に示します。赤文字のところで数字が変わります。
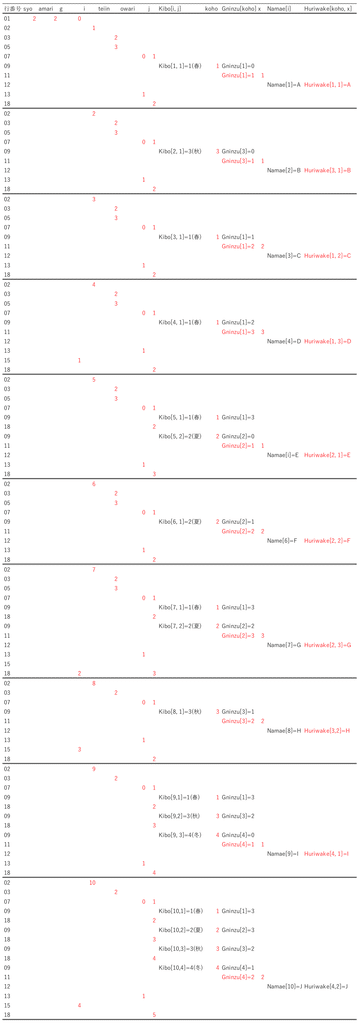
図1のプログラムの行と照らし合わせながら確認してみてください。
画質が落ちて見辛いと思いますので、エクセルファイルをダウンロードしてお使いください。
問3
問2同様にトレースしながら確認してみてください。
実際にPython等の言語でプログラミングしてみると一層理解は深まるかと思います。

第3問はかなり難易度は高めでしたね。もう少し使う変数や配列が少ないと良かったのですが…
第3問を選んだ方の平均点は低いのではないでしょうか。
第4問(選択)
難易度は優しめでした。
今回の問題では第3問を選ぶよりは第4問を選んだ方がいいかと思います。(試験中にはなかなか判断できませんが…)
平成30年の問題のように、エクセルで再現しようかとも思ったのですが、流石に600人分の架空のデータを作って辻褄を合わせるのは途方もない作業になりそうだったので断念しました。すみません。
問1
ア : ②AVG(D2~F2)
イ : ③SUM(G2~I2)
ウ : ②$B$2~$B$601
エ : ①$A2
オ : ⑦J$2~J$601
カ : ⑤$C$2~$C$601
ア~イ
3日間の平均睡眠時間とあるので、シート1生活習慣調査のD, E, F列の3日間の睡眠時間の平均をとるのでAVG関数を使います。
AVG関数はエクセルだとAVERAGE(数値1, 数値2, …)と入力しないといけませんが、情報関係基礎ではAVGと略してあります。
また、範囲の指定もエクセルだと「D2:F2」のように表すところを情報関係基礎では「D2~F2」のように表すのも若干の注意が必要です。
アの正解はAVG(D2~F2)です。複写しますがJ3~J601に複写とあるので行が変わります。
同じ行にあるD2, E2, F2の平均値が欲しいので「$」は必要ありません。
J2がAVG(D2~F2)で、J3に複写するとAVG(D3~F3)のように数字が変化します。
イでは、三日間の朝食回数を計算とあります。平均ではないので注意。
朝食を食べた回数の合計を求めるので、SUM(G2~I2)が正解となります。
COUNTでは、セルに数字が入っている個数を返すので、1でも0でも同じ(この場合3)が返ってくるので、朝食を食べた回数の合計が求められません。
ウ~オ
次に求めるのは学年別の平均です。
セルB2は1年生の平均睡眠時間なので、
AVGIF(生活習慣調査!$B$2~$B$601, A2, 生活習慣調査!J$2~J$601)が正解です。
AVGIF(セル範囲1, 式, セル範囲2)はセル範囲1のなかで、式と等しい値をもつセルに対応するセル範囲2の中の平均値を返します。
今回は、生活習慣調査のシート1の列B(学年)がA2のセル(1)と等しいものを見つけて、同じ行のJ列(個人平均睡眠時間)の値の平均値を返します。
B3, B4に複写とあるので、範囲(行)が動かないようにB$2~B$601とし、
さらにC2~C4にも複写とあるので、範囲(列)も動かないよう$B$2~$B$601となります。
カ
シート3では距離別の平均を作成します。ここでも先ほどと同様AVGIFが登場します。
AVGIF(生活習慣調査!$C$2~$C$601, A2, 生活習慣調査!J$2~J$601)が正解です。
今回も、複写するのですが範囲が動いてしまっては困るので範囲指定は$C$2~$C$601となります。
問2
キ : ③MEDIAN
ク : ③7.0
ケ : ④A2
コ : ②2
サ : ③COUNTIF(3年生!$B2~$B201, B1)
シ : ③睡眠時間が7.0以上の生徒については、睡眠時間が増えるにつれて睡眠時間ごとの生徒数が減少する。
ス : ①6.5以下
キ・ク
これらは関数知ってる?という問題でした。しかし、情報関係基礎の場合後ろに関数の説明はバッチリ載っているのでこれを問題にする必要はあるのでしょうか…。

キは選択肢のINT, COUNT, MODE, MEDIANから中央値を求めるMEDIANを選べばOKです。
最頻値をもとめるのはMODEなので、シート5のB4にはMODE(3年生!A2~A201)が入力されているはずです。そこで求められた値が7.0となっているので3年生で一番多い睡眠時間は7.0時間だったということですね。
絶対に落とせない点取り問題でした。
ケ・コ
0.5時間単位で小数部分を切り捨てた値を求めます。
INT(式)は式の値を超えない最大の整数を返す関数です。例をあげればINT(6.5)などの場合6になるということですね。
しかし、そのままINT(A2)などにしてしまうとかなり値に誤差が生まれてしまいます。
どういうことかというと、今回A2の値は6.7ですが、INT(A2)とすると6になってしまいます。極端な話、6.1も6になりますし、6.9も6になってしまうわけです。
これでは統計として信頼のできる結果とは言い難いです。
そのため、一旦値を2倍にして、2倍された値をINT()して、また2で割るということをします。これをすることで、誤差を少なくすることができます。
B2の場合、INT(6.7*2)/2で6.5となります。
実際にエクセルで統計を出すときはROUND関数等を用いて四捨五入することが多いかと思いますが、情報関係基礎や情報処理技術者試験では今回のような方法を取られることが時々あるので覚えておくといいかと思います。
サ~ス
サ~スは表とグラフを見ながら答える問題でした。
シート6セルB2には、睡眠時間がB1(5.0時間)と一致する生徒の人数を数えるため、COUNTIF関数が入ります。
SUMIFだと条件に合う中に入っている数値の合計が返されてしまいます。
しかも、A列から5.0時間と合致するのを見つけるというのはおかしな話ですよね。
②と③で迷うかと思いますが、今回はC2~L2に複写するとあるので、複写した時に列がずれてしまわないよう$B2~$B201とする必要があります。
$がないと、複写した時C2~C201のように存在しない列を参照してエラーが出てしまいます。
問3
セ : ⑥F$2
ソ : ⓪A2
タ : ②24
チ : ③D2~D601
ツ : ⓪睡眠時間と朝食の間に正の相関がある。
テ : ④経過時間は、睡眠時間との間に負の相関があり、朝食との間にも負の相関がある。
セ~タ
経過時間を求めます。
正解はA2*60+B2-F$2*60+IF(F$2>A2, 24*60, 0)となります。
まず経過時間を分単位で表すために、A2*60+B2で就寝時刻(時)を分にします。
21時からの経過時間(分)を求めるので、基準となる21が記載されているF2*60を引きます。(-F$2*60)
23時台まではここまでのA2*60+B2-F$2*60の式で大丈夫なのですが、0時以降はこの式だとマイナスの値になってしまいます。
なので、IF(F$2>A2, 24*60, 0)で、21時より小さい値(0時以降)の場合に24*60分をプラスするようにします。
600行目を使って考えてみましょう。

A2*60+B2-F$2*60+IF(F$2>A2, 24*60, 0)
就寝時刻(時)が0なので、0*60+25-21*60=-1235です。経過時間を知りたいのにマイナスだと困ります。
0は21より小さいので、IF文が真の時に実行される24*60がプラスされ、セルC600には205が入ります。
チ
相関関係を求めるのにCRREL関数を用いています。
CRREL関数を実行すると相関係数を求めることができます。
相関係数=Correlation coefficient(コリレーション コフェシエイト)から来ています。
経過時間と睡眠時間の相関関係を調べ、経過時間と朝食の相関関係も調べるためにB2に複写したとあるので、
CORREL(再調査集計!$C2~$C601, 再調査集計!D2~D601)が正解です。
$D2~$D601としてしまうと、複写しても範囲が変わらず経過時間と睡眠時間の相関関係が表示されてしまいます。
<おまけ>
C2にはCORREL(再調査集計!D2~D601, 再調査集計!E2~E601)が入力されています。
ツ・テ
ツ・テは一つ一つ内容をみて合っているか合っていないか確認していけば解ける問題でした。

参考文献等
※本記事は2019.01.21にtkmium.techで公開したものを移行したものです。
「情報関係基礎」の問題は(独)大学入試センターから掲載許可を得て解説を作成しています。問題および解答の著作権は大学入試 センターに帰属します。
解説の文章および画像等を無断で転載することはお控えください。
質問や誤植のお知らせ、その他連絡につきましてはコメント欄またはTwitterからお願いいたします。
ブログで公開していた時にいただいていたコメント
ゆひぐまさん より: 2022年4月7日
質問失礼します。
第一問 問2 テの回答が③になるのはなぜですか?
論理演算の問題に不慣れで、用語の解説などを調べたのですがわかりませんでした>_<
「AとCの論理和になる」というのがどういうことなのかいまいち理解できません泣
私の理解↓
XOR回路
・2つの入力が等しい場合は0を、異なっている場合は1を出力する)になっている。
論理和
・2つのうちどちらか、あるいは両方が真であれば真。
この記事が気に入ったらサポートをしてみませんか?
