
【解説】情報関係基礎 令和3年度 共通テスト 2021 1次日程

第1問(必答)
問1
ア(正解:6)
62種類の文字を全て区別して符号化するには何ビット必要かという問題です。
このような問題の時は、以下の表を書くのでしたね。

26が64なので、6ビットあれば62種類の文字を符号化できます。
イウエオ(正解:1440)
計算式は、800 × 600 × 24 ÷ 8 ÷ 1000 = 1440となります。
この場合、800 × 600個の画素があり、それぞれが24ビットフルカラーで表現されます。
8ビット = 1バイトなので、8で割ってバイトにして、
1kB = 1000バイトという条件があるので、また1000で割ります。
カキクケ(正解:1800)
動画のデータ量に関する問題です。
30fpsとあるので、1秒間に30フレーム(30枚の画像)分のデータ量です。
よって、1分間の動画の場合は、30(フレーム) × 60(秒) = 1800。
1440kB × 1800のデータ量となります。
コサ(正解:32)、シ(正解:1)
IPv4と呼ばれる規格のIPアドレスは、インターネット上の住所であるIPアドレスを、32ビットの2進数で表現します。0と1の羅列では、人間が理解できないため、これを10進数に変換し、8桁ずつ4つに区切った「ドットアドレス」で表記することがほとんどです。
また、このIPv4アドレスは、32ビットなので、つまり2の32乗個=約43億個しか使うことができません(実際にはテスト用など使えないものもあるのでもっと少ない)。現在の世界人口が77億人ほどとされているので、1人1IPアドレスでも全然足りない計算になります。
そこで登場したのが128ビットで表現する IPv6です。
2の128乗は約340澗個。これは地球上のチリやホコリにまでIPアドレスを振ることができるとさえ言われています。
IPv6は、IPv4の4倍の長さを持つので、IPv4のような10進表記ではなく、16進数で表現し、「:(コロン)」で区切ります。
スセ(正解:58)
著作者人格権には、公表権・氏名表示権・同一性保持権があり、著作財産権には、複製権・上映権・演奏権・上演権・公衆送信権・口述権・展示権・頒布権・譲渡権・貸与権・翻訳権などがあります。
財産権については全て覚えておく必要はありませんが、人格権については必ず押さえておきたいですね。
問2
ソ(正解:5)、タ(正解:0)
ラスタ画像とベクタ画像に関する問題でした。説明は問題文にある通りです。
平成28年にも出題がありました。

チ(正解:2)
これは間違いようがない問題でした。
“バックアップ”なので、今データを保存している媒体とは別のものにデータを保存します。
問3
ツ(正解:2)
6等が当たるには下1桁さえ当たれば良いです。
そのため、最低でも10人(0~9までをそれぞれ送る)に送れば誰かは当たります。
テ(正解:4)
5等は下二桁だそうです。
2桁の10進数は00から99まで、102=100通り表されます。よって100人に送れば良いです。
ト(正解:7)
ツ、テより、6等が当たる確率(前回)は1/10、5等が当たる確率(今回)は1/100ということがわかりましたので、その両方が当たる確率は1/10×1/100=1/1000となります。
よって最低でも1000人に送れば1人は当たる計算になります。
ナ(正解:1)
フィルタリングに関する問題でした。
ホワイトリスト、ブラックリストなど、フィルタリングに関する用語も合わせて押さえておきましょう。
ニヌネ(正解:482)
公開鍵暗号方式、デジタル署名に関する問題でした。
公開鍵暗号方式は、送信者が受信者の公開鍵でメッセージを暗号化し、受信者は受信者の秘密鍵で受け取った暗号メッセージを復号します。
逆に、送信する際に、秘密鍵で暗号化して送信し、公開鍵で復号してもらうことによって改ざんされていない本人が送ったメッセージであることを証明する手法をデジタル署名と言います。
公開鍵で暗号化するのか秘密鍵で暗号化するのかわからなくなってしまわないように注意が必要です。南京錠をイメージするとわかりやすいと思います。
第2問(必答)
問1
アイ(正解:20)
30枚比較した時点で10分とあるので、10×60/30=20ですね。
ウ(正解:3)
比較の作業にT時間かかるそうですが、工夫1をすることで、1回の比較の時間が1/4になるそうです。よって工夫1をすれば、T/4時間で比較できます。
これに、メモを貼る時間の1時間を足すので、1 + ( T /4 )時間が正解となります。
エ
工夫2では、工夫1で作成したメモに書かれた4個の数字を4桁の数とみなして、数の小さい順に絵を並び替えます。
ここで、前提条件を復習しておきます。
色は9色ある
それぞれの子供は4本ずつもらった
子供がもらった4色は全て組み合わせが異なる
子供は60人、絵は全部で200枚
それぞれの子供は少なくとも3枚の塗り絵をした
ここでは、同じ色の組み合わせで塗られた絵は同じ子が塗ったとして扱います。
実際に並べ替えてみると、同じ色の組み合わせの絵が、連続して(隣り合って)現れることが考えられます。
塗った絵は、少なくとも3枚なので、4枚以上現れることも考えられますし、以降の問題で出てくる、使う色を減らして(2色や3色で)塗っている子も考えられるので3枚おきに現れるは間違いです。
オ(正解:1)
最初問題の意味がわからずに戸惑いました。途中いくつも、分類や比較という言葉が出てくるので、この場合の分類とはどの作業を指すのか…?となりました。
が、まず問1で、「色の組み合わせが同じである絵を探すために、試しに1枚の絵を手に取り、使われている色を他の絵と比較していくと…」とあるので、2枚目から200枚目までを、一つ一つ比較していくんだなというのがわかります。
まず1枚目をAさんが描いた絵(色の組み合わせ)としておいて、2枚目がAさんの色の組み合わせと同じであるのかを比較し、違うならばその色の組み合わせはBさんとする。3枚目以降も同様に、Bさんと同じ色の組み合わせならばBさんの絵に分類し、違うならCさんとする…という風に比較・分類していくということですね。
同じ色の組み合わせが連続して(隣り合って)出現するはずなので、つまり、1つ前の絵との色の組み合わせを確認すれば良いということになります。
最初の絵は比較する絵がありませんので、残りの(200-1)枚分をその一つ前の絵と比較すれば良いということになります。
よって、1回の比較にかかる時間は、20/4秒とわかっているので、(200-1)×20/4秒が正解になります。
問2
カ(正解:2)
残り12枚で残り4人ですので、前提条件の「それぞれの子供は少なくとも3枚の塗り絵をした」という条件から、②が正解です。
キ(正解:3)
4人の子供で12枚、かつひとり3枚以上という条件から、4人全員が3枚ずつになります。
この場合は、子供WはAからFの絵の中から3枚を塗ったことになります。
クケコ(正解:1-4-5)、サ(正解:5)
子供Y、Zについても可能性のある絵を線で結ぶとこのようになります。
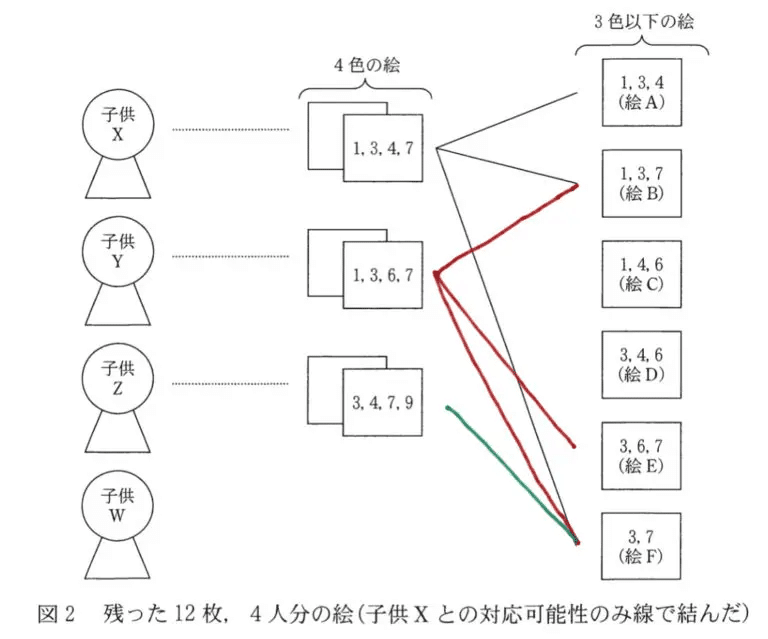
子供X、Y、Zは4色持っているので、その4色の中から表現可能な3色以下の絵を見つけます。
すると、子供Yが塗った可能性がある絵はB、E、Fであり、子供ZはFのみとなります。子供ZはFのみとなりましたので、ひとり3枚という条件から、絵Fは子供Zの描いた絵と断定できます。
シ(正解:2)、スセソタ(正解:1-3-4-6)
先程の図から、子供X、Y、Zが塗った可能性がない絵が2枚見つかります。絵Cと絵Dです。
これに使われているのは、1、3、4、6の4色です。
チ(正解:0)
1、3、4、6の4色で子供Wに塗られた可能性があるのは、絵Aしかないので、子供Wの絵は、A、C、Dであるとわかります。
ツ(正解:1)、テ(正解:4)
子供Xの可能性がある絵は、A、B、Fでしたが、絵Aは子供W、絵Fは子供Zに決まってしまったので、必然的に子供Xの絵はBとなります。同様に、子供Yの絵はEと決まります。
第3問(選択)
この問題は簡単ですし、イメージもしやすかったですね。
問1
ア(正解:7)、イ(正解:6)、ウ(正解:5)
表2に値を入れいくとこのようになります。

崖、穴、沼それぞれ条件がありますので、間違いに注意して埋めていけば解ける問題でした。
エ(正解:4)
コマNはラウンド5の時点で、12(沼)にいるので、6を出せば、3進むことができて15(ゴール)にたどりつけましたが、4を出してしまったので、2進んで14崖についてしまっています。
問2
オ(正解:7)、カ(正解:1)、キ(正解:8)、ク(正解:9)
出た目から、移動さきのコマの位置を算出するプログラムです。
まず、(01)〜(04)で初期化を行っています。
(03)のKoma[i, r]←1 では、プレーヤー全員のラウンド0での位置を1(スタート地点)に設定していますね。
(05)からは実際の処理です。
(06)でラウンドを+1しています。
(09)では、1つ前のラウンドでのコマの位置をkに代入しています。
(10)では、(09)でkに代入したコマの位置を使って、そのマスの効果値をbairituに代入しています。この効果値は、道マスなら1、崖マスなら-1、沼マスなら0.5、穴マスなら0が入ります。
(11)〜(13)では、(10)の処理後、もしbairituに0が入っている、すなわち穴マスの場合に、出た目によってbairituを変える処理が入っています。穴マスは、出た目が4以上なら出た目の数だけ前進するので、bairituが0かつ、Saikoro[i, r]が4以上ならば、bairituに1を代入します。
(14)では移動するマス数を調べています。マスの効果値(bairitu)と出た目(Saikoro[i, r])の掛け算で求められます。ただし、小数点以下は切り捨てるそうです。
(15)では実際にコマを移動させます。一つ前のコマの位置であるkに、(14)で求めた実際に移動するマス数であるidouを足します。
(16)〜(19)は、スタート地点やゴール地点よりも前や後ろになってしまった時の処理が書かれています。

問3
オバケが可愛いですね笑
今回は、友人のSさんがスゴロクを面白くするためにオバケ👻を登場させたそうです。
「コマがゴール方向にオバケを追い抜こうとするとオバケに捕まる」という処理が追加されています。
問3は図3にプログラムが全て書いてあるので、トレースできれば正解できる問題でした。
ケ(正解:8)、コ(正解:7)、サ(正解:1)、シ(正解:6)、ス(正解:7)
表4を全て埋めると以下のようになります。

トレースしてみると、おばけは6〜8の間を行ったりきたりしていることがわかります。
コマの位置ですが、ラウンド4でオバケと同じマスになって、ラウンド5、6はオバケがゴール方向に動くので、毎度捕まります。そのため、ラウンド7でオバケがスタート方向に動くまではオバケと同じマスまでしか進めません。
第4問(選択)
問1
ア(正解:0)
重複する下位の回答を無効にする処理です。
セルG2は2位が1位と同じかどうかを判断します。
セルC2とD2が同じであれば「×」を表示するので、式は IF(C2 = D2, “×”, D2)となります。
イ(正解:7)、ウエ(正解:2-4)
セルH2に入れるのは、3位の回答が1位や2位と同じかどうかを判断する式ですね。
そのため、IF(OR(E2 = C2, E2 = D2), “×”, E2)となります。
E2に入っているのは3位の回答ですね。このE2がC2(1位)と同じか、または、E2がD2(2位)と同じであれば、「×」を表示して、そうでない場合はそのまま表示します。
オ(正解:0)、カ(正解:5)
満足度割合を出したいそうです。
例えば、シート2満足度別人数のB列に入っている、満足〜不満までの人数を全て足したもののうち、満足の割合を求めたいわけです。
ので、シート3のセルB2に入るのは、 満足度別人数!B2/SUM(満足度別人数!B2~B6)*100 となります。
これを複写するわけですが、右方向に複写する時(2018年度、2019年度…)は範囲もズレて複写してほしいですが、下方向に複写するとき(やや満足、普通…)は合計の範囲はズレて欲しくありません。
そのため、SUM(満足度別人数!B$2~B$6)と範囲を固定することになります。
セルB2~B6とあった場合、$B2~$B6とすれば列が固定され、B$2~B$6とすれば行が固定されます。これを相対参照と言いました。
よって正解は満足度別人数!B2/SUM(満足度別人数!B$2~B$6)*100 です。
問2
キ(正解:5)、クケ(正解:2-6)
高校生、中学生、小学生それぞれの満足、やや満足、普通、やや不満、不満の総数を求めるため、調査回答の回答者区分と満足度だけを取り出しています。
相対参照の$の位置を考えるのがやや面倒ですが、難しくはありません。
正解は IF(AND($A3 = C$1, $B3 = C$2), 1, 0) です。
C3に入れた上記の式をC4〜C242とD3〜Q242に複写するわけですが、横方向に複写した時A列B列は変わって欲しくありません。また、縦方向に複写した時1行目2行目は変わって欲しくありません。
そのため、$A3、$B3、C$1、C$2となります。
コ(正解:0)
シート5はシート4の集計結果ですね。
シート5のB2には、高校生で満足した人数の総数が入ります。
高校生で満足の人数は、シート4のC列に入っているので、計算式はSUM(チェック用!C3〜C242)となりますね。
COUNTやCOUNTAを選んでしまった人がいるかもしれませんが、COUNTは範囲のうち数値のセルの個数を返して、COUNTAは空白ではない数値の個数を返す関数です。
例えば、今回の場合はCOUNTIF関数であれば同じような処理をすることが可能ですね。
COUNTIF(チェック用!C3〜C242, 1)
サ(正解:1)
高校生全体の人数から、「満足」の人の割合を求めるためには、「満足」と回答した高校生の人数を、高校生全体の人数で割ればいいですね。
よって、①の「満足」と回答した高校生の人数を、シート5のセルG2で割ることにより求められるが正解です。
問3
シ(正解:2)
シート6には、それぞれの企画で1位、2位、3位を選んだ人数を表示します。
COUNTIF関数が使われていますね。セルB2に入れる式は COUNTIF(調査回答2020!F$2〜F$241, $A2)です。
COUNTIFの検索条件には、シート6の企画名が入るわけですが、これも、縦方向の複写はOKですが、横方向へは動いて欲しくないので、列を固定して、$A2となります。
スセソタ(正解:8, 5, 3, 2)
企画ごとの各順位の得点を求めたいようです。
例えば、シート8のセルB2には、カフェで1位を選んだ人数(47人)×1位の得点(30)=1410が入るようにします。
セルB2に入る計算式は、 順位人数!B2 * VLOOKUP( B$1, 得点表!$A$2〜$B$4, 2) です。
シート8とシート6はA1〜E8まで同じ並びなので、縦方向横方向どちらも固定する必要がありませんので、順位人数!B2。これにシート7で定めている各順位の得点が掛けるように設定すれば良いです。
シート8のセルB1, C1, D1に1位、2位、3位と入っているので、それを得点表から見つけてきます。
まず、見つけてくるセルB1, C1, D1は、縦方向に動いて欲しくないので、B$1と行を固定します。
得点表の方は、A2〜B4のセルは全く動いて欲しくないので縦方向横方向両方を固定する絶対参照にします。
チツ(正解:3, 7)
RANK関数についてでした。
各合計得点が範囲のうちの何位なのかを返す関数です。
F2に入る式はRANK(E2, E$2〜E$8)となります。
F3〜F8にしか複写しませんので、範囲の縦方向を固定するだけでOKです。
参考文献等
※本記事は2021.01.19にtkmium.techで公開したものを移行したものです。
「情報関係基礎」の問題は(独)大学入試センターから掲載許可を得て解説を作成しています。問題および解答の著作権は大学入試 センターに帰属します。
解説の文章および画像等を無断で転載することはお控えください。
質問や誤植のお知らせ、その他連絡につきましてはコメント欄またはTwitterからお願いいたします。
この記事が気に入ったらサポートをしてみませんか?
