
なぜ相対性理論により同時性が破綻するのか
ここでは、特殊相対性理論を知らない人向けに簡単にこの理論の概要を説明した後に、同時性の破綻という直感に反する現象を説明しようと思う。
1905年に発表されたアインシュタインの特殊相対性理論は現代物理学の基礎を成している。相対性理論といえば、特殊相対性理論と一般相対性理論がある。理系ではない人の考え方からしたら、「特殊相対性理論の方が一般相対性理論より難しのでは?」と思うかもしれない。これは実は逆で一般相対性理論の方がとても難しい。実際、一般相対性理論が発表されたのは1916年でこれは特殊相対性理論の発表より遅い。私もこれから一般相対性理論を勉強していこうという身である。一応簡単にこの二つの理論で何が違うのかを説明していくとすれば、一般相対性理論は特殊相対性理論にさらに重力の効果も含めて説明しようとした理論である。
特殊相対性理論によれば、さまざまな直観に反する結果が導かれる。その一つに同時性の破綻がある。同時性の破綻とは、ある観測者が同時だと観測した二つの事象が別の観測者には同時には観測されないことがあるということである(後で詳しく説明する)。これを特殊相対性理論の原理から考えていこうと思う。特に数学を使うわけではないので、内容的には中学生でも理解できるはずだが、とにかく直感に反してくるのでなかなか難しい。
まず、特殊相対性理論とは何かについて説明する。まず、いくつかの用語について説明する。正直、用語をきちんと理解しなくても相対性理論の気持ちは理解できると思うので、用語の説明が難しければ、飛ばしてしまっても構わない。
基準系とは、自然のなかで生じるいろいろな過程を記述するものであって、粒子の位置を指定するためのxyz座標系と、時刻を指示するためのその系に固定された時計とを合わせたものである。ここで基準系の定義に時計なるものが入っていることに注意してほしい。時計が入っていないものはイメージしやすいかと思う。xy座標系をイメージしてほしい。これを地面の上に置けば、地面を動く物体の位置を記述し(x座標とy座標を測定すればよい)、すなわち、物体の運動を記述することができる。さらに、一般に空間の中にxyz座標系を配置すれば、空間を飛び回る物体の運動の位置を記述することができる(x座標、y座標、z座標を測定する)。相対性理論はそのxyz座標系に時計を追加する。これは基準系を取り替えたときに二つの時計の進み方が変わるためであるが、これがまさに同時性の破綻と関係している。
次に慣性基準系について説明する。慣性基準系とは、慣性の法則が成り立つ基準系である。慣性の法則とは、力が働かない物体は静止するか、等速直線運動をするという法則である。この法則が成り立つ座標系を慣性基準系というのである。「慣性の法則はどんなときでも成り立つんじゃないの?」と思った人には、慣性の法則が成り立つ基準系(K系と呼ぼう)に対し、加速度運動する基準系(K'系と呼ぼう)を想像してほしい。そのK'系で力が働いていない物体の運動を観測すると、加速度運動して見える。なぜなら、K系では物体は等速直線運動しており、そのK系に対しK'系は加速運動をしているからである。
慣性基準系は無数に取ることができる。なぜなら、慣性基準系に対し等速直線運動している基準系では慣性の法則が成り立ち、すなわち、慣性基準系であるからである。
用語の説明ここで終わり
では、特殊相対性理論の原理について説明する。特殊相対性理論では次の二つの原理をおく(物理学における原理とは、それらを仮定すると、物理現象が説明することができる、というものである)。
すべての物理法則は、任意の慣性基準系で同じ形をとる。
光の速度は光源の運動によらず一定であり、さらにそれは、時・場所によらない普遍な値をとる。
この原理がなぜ成り立つかを問うのは、ひとまず置いておこう。なぜなら、物理における原理とはそれを仮定することにより、実際に物理現象が説明できるか、が重要であるからである。実際、この原理からスタートする特殊相対性理論はさまざまな物理現象を説明できることが知られており、さらに相対性理論をベースとして考案された技術が私たちの生活を支えているからである(例えば、原子力発電)。
一つ目の原理は慣性基準系といういい性質をもった基準系を考える限り、それら全ての上で物理法則は同じ形をとるということである。
二つ目の原理は、一つの慣性基準系のなかでどのように光が出されても、その速さは一定値を取るということを言っている。光速はそれが出てきた光源の運動によらず普遍な定数 c = 約2.998×10^8 m/s という値をとるということである。
一つ目の原理と二つ目の原理を合わせて考えてみよう。二つ目の原理によれば、ある慣性基準系では光速は普遍な値 c = 約2.998×10^8 m/s をとるという物理法則がある。ここで一つ目の原理から、この物理法則はどんな慣性基準系でも同じである。つまり、光速はどんな慣性基準系でも変わらない。
これはどういうことか。簡単に言えば、光速はどんな等速直線運動をしている人から見ても同じ値をとるということである。
これがとんでもないことを言っていることに注意してほしい。あなたが光速の半分の速さで動いていることを想像してほしい(これは大体1秒で地球を3周ちょっとする速さであるが想像力を膨らませてほしい)。そしてあなたが等速直線運動で光を追いかけているとしよう。素朴な考え方では、このとき光は c / 2 の速さで運動していると思うであろう。この素朴な考え方とは、時速60km で動く電車をあなたが時速20km で追いかけたら、あなたは電車が時速40km で動いているように見えるという考え方から来ている。特殊相対性理論はこの素朴な考え方を否定する。なぜなら、あなたは等速直線運動をしているのだから、あなたからみても光は一定値c の速さで遠のいていくのだ。
このように光速が観測者に応じて変わることがないのは、かなり直感に反する。しかし、実際のところ、光速の不変性は現在では高い精度で確かめられている実験事実である。さらに、先にも説明した通り、特殊相対性理論の原理から得られる帰結は、実際の物理現象を説明している。私たちはこの原理を認めるしかないであろう(個人的には認めるしかないというネガティブなものではなく、ぜひとも認めていきたい美しい理論である)。
では、さらにもう一つ直感に反する現象であり今回のテーマ、同時性の破綻を見ていこうと思う。この同時性の破綻は私自身が特殊相対性理論を学び始めた大学2年生の頃、それが成り立つことに気づかずに勉強を進めており、途中で成り立つことに気づき、一気に特殊相対性理論の一種の凄さを体感したものである。
同時性が破綻するとは、ある慣性基準系K系では同時(K系に置かれた時計で同じ時刻)に起きた事象が別の慣性基準系K'系では同時ではない(K'系に置かれた時計で同じ時刻ではない)ということが起きるということである。簡単にいえば、ある観測者が同時と観測した二つの事象が別の観測者は同時には観測されない、ということである。これはニュートンの時代から当たり前のものとされてきた時間の絶対性を否定するものである。つまり、異なる基準系では時間の流れ方は異なるということを端的に示すのである。簡単にいえば、動いている人と止まっている人では時間の流れ方が違う、ということである。
では、これが成り立つ理由を考えていこう。図1のようにそれぞれ座標軸xyz およびx'y'z' をもつ二つの慣性基準系K系とK'系を考える。K'はKに対してx軸(x'軸) に沿って運動しているとする。x'軸上の点Aから互いに反対方向に二つの光が出たと考えよう。
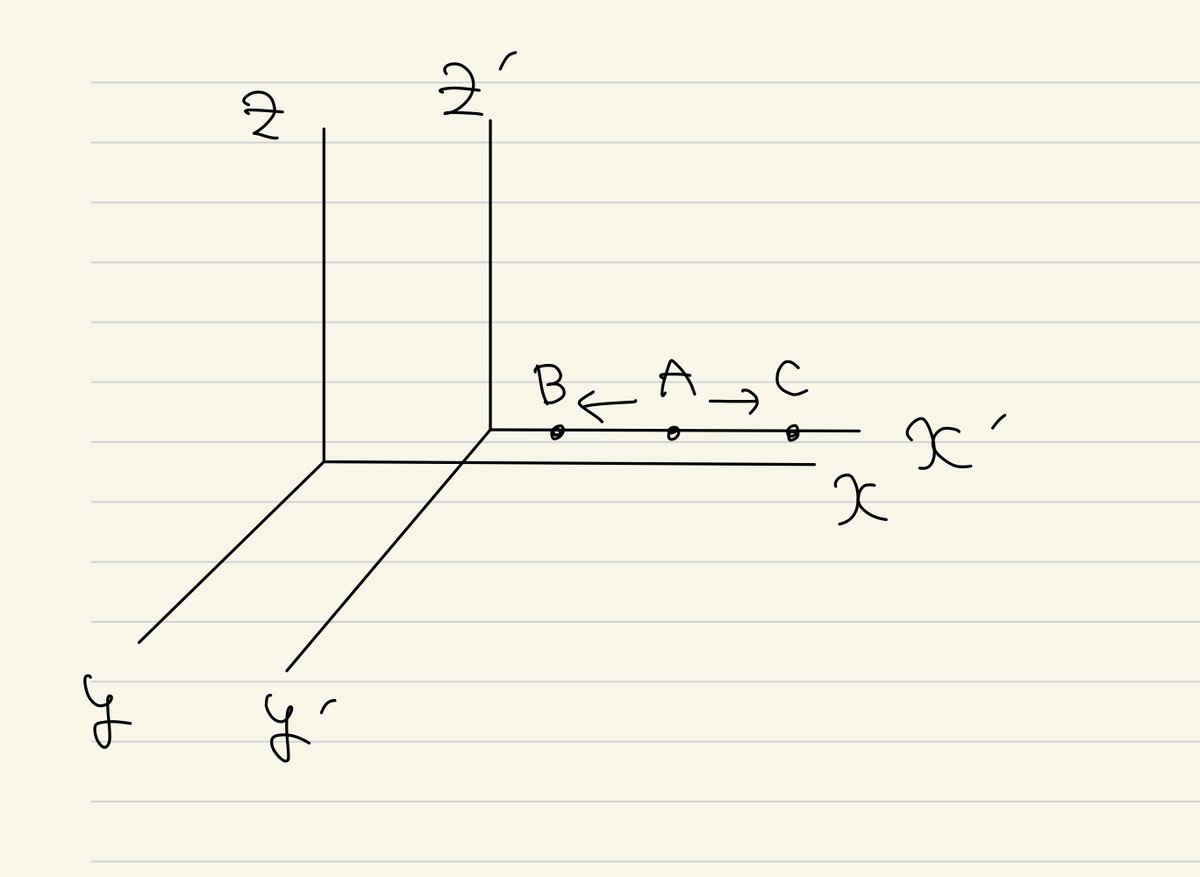
二つ目の原理から、光速はどんな方向にも一定値cだから、K'系においてAから等距離にある点Bと点Cには、同時に光は到達する(3点A、B、Cはx'軸に固定されていることに注意してほしい)。一方、同じ状況をK系で観測する。二つの原理から導かれた結論により、K系においても光速の値は一定値cである。しかし、K系において光がそれぞれBおよびCに到達する時刻は同時になり得ない。なぜなら、K系においてBはAが光を出した位置に向かって、CはAが光を出した位置から離れるように動くので、光は点Cに届くより早く点Bに到達するからである。
このようにK'系において同時に起きた事象がK系では同時でないことが分かった。このように特殊相対性理論は私たちが当たり前だと思っている日常的な認識に根本的な変更を強いるのである。
では最後に、なぜ私たちが日常生活で培った直感は、こうも相対性理論の帰結と矛盾するのだろうか。それは、光速が私たちの日常的に感じるスピードに対して非常に速いからである。例えば、同時性の破綻を考えた時の状況を考えてみよう。より日常に近づけるためにK系を地面の上で静止した観測者、K'系を電車に乗った観測者と考えてみよう。このとき、K系でBがAのいた位置に近づく速さ、CがAのいた位置から遠ざかる速さというのは、光速から比べると微々たるものである。実際例えば、電車の速さを時速100km としてみよう。これは約28m/s である。これに対して、光速は約3x10^8 m/s である。よって、K系でもK'系でもBとCに光はほぼ同時に到達し、日常的なスケールでは地面にいる人が電車に乗っている人との同時性の破れに気づくことはまずないのである。
参考文献
風間洋一 『相対性理論入門講義』 培風館(2022)
シュッツ(江里口良治・二間瀬敏史 共訳) 『シュッツ相対論入門』 丸善(2010)
ランダウ・リフシッツ(恒藤敏彦・広重徹 共訳) 『場の古典論』 東京図書(1987)
この記事が気に入ったらサポートをしてみませんか?
