カーネル関数をゆるふわに掴む(1/2)

tanuki

前々回と前回、「カーネル多変量解析」の第一章をコード書きながら理解しようとしました。まぁゆるふわに理解できた気がします。

今回は第二章です。主にカーネル関数とは何か？的な話です。

このシリーズの目次はこちら

第一章の復習

サンプルデータがn個あるとします。一つ一つのサンプルデータは、複数のパラメータ（特微量）を持つ$${x^{(i)}}$$と結果の$${y^{(i)}}$$からなります($${i=1,2,…,n}$$)。

そのサンプルデータを説明するような関数$${f(x)}$$を作れたら、未知のデータ$${x^{(new)}}$$に対応する$${y^{(new)}}$$も予想できるので嬉しいです。

例：n個のフルーツ$${x^{(1)}, x^{(2)}, …,x^{(n)}}$$を食べて、$${x^{(i)}}$$の「色」と「形」と「匂い」という特微量から$${y^{(i)}}$$「味」が予想できるようになると、未知のフルーツ$${x^{(new)}}$$の味$${y^{(new)}}$$が予想できるので食べるかどうか判断できて嬉しいです。

カーネル法は、以下の手順で簡単に関数$${f(x)}$$が作れちゃいました。

  1. どこかからやってきたカーネル関数$${k(x, x')}$$を使って、サンプルデータの全組み合わせに対してその値を全部計算、並べて行列$${K}$$を作る

  2. どのくらい汎用的な関数にしたいか係数の$${\lambda}$$を適当に決めて、$${K-\lambda I}$$を計算する（ただの引き算）

  3. サンプルデータの答え一覧である$${y}$$を使って、$${\alpha = (K-\lambda I)^Ty}$$を計算する（ただの内積）。これで$${f(x)}$$完成

  4. 未知の$${x^{(new)}}$$に対して、各サンプルデータ$${x^{(i)}}$$との$${k(x^{(i)}, x^{(new)})}$$を計算し、重み$${\alpha_i}$$を掛ける。それらを足し合わせると未知の$${y^{(new)}}$$に得られる

この記事のゴール

前回棚上げになったカーネル関数$${k(x, x')}$$＝近さの関数って何？を説明してみたいと思います（理解しようと試行錯誤した結果、本とだいぶ違う説明になっています）。

カーネル関数の「近さ」とは何か

第一章でお話しした式はこうでした。
$${y_{(pred)} = \sum \alpha_i k(x^{(i)}, x)}$$

カーネル関数$${k(x, x')}$$は$${x, x'}$$の「近さ」を示す関数でした。関数に$${x^{(new)}}$$を与えると、各$${x^{i}}$$との「近さ」から$${y^{(new)}}$$を求めました（「近さ」に対する重み付けが$${\alpha}$$で、それをサンプルデータから学習しました）。

この「近さ」とは何か？が最初の論点です。

例として、$${x = (x_1, x_2)}$$から$${y}$$を求めるモデルを考えてみます。$${x_1, x_2}$$は数値ですが、$${y}$$は黄色、青、緑のいずれかです。サンプルデータを散布図に書くとこんな感じだったとします。

x1, x2から色yが決まる

ここで、下の赤い点の$${x^{(new)} = (x^{(new)}_1, x^{(new)}_2)}$$が与えられたときに、$${y^{(new)}}$$は何色になるでしょうか？

それぞれ赤いバツの色を予想してみる

左右共、赤バツの色を予想するときは、$${x^{(new)}}$$と各$${x^{(i)}}$$との「近さ」を全て計算して、重み付け$${\alpha}$$を掛けて推定します。

左の図は、赤バツの周りに黄色点が多く、複数の黄色点との「近さ」が大きいため、（重みにもよりますが）青や緑の点との「近さ」の影響は相対的に小さくなり、予想値は黄色になるだろうと考えられます。

一方、右の図は、赤バツの周りに青も緑もあり、それぞれ「近さ」が大きいので、どちらになるか難しいところです。各点との重み付けによって結果が変わります。もしサンプルデータが増えると、結果も簡単に変わりそうです。

さてここで、この右の図を三次元に変えてみます。とはいえ変数は$${x_1, x_2}$$しかないので、それらから3次元目を作ります。ここでは$${sin(x_2\pi)}$$を3次元目とします。

3つ目の軸を追加

こうすると、赤バツの周りには緑点が多くなり、緑点との「近さ」が増えるのでおそらく赤バツは緑になるだろうと予想されます。

まぁ出来レースだったんですけど、元の特徴量から別の特微量を作ると綺麗に分離するのは面白いです。これを特微抽出というそうです。この変換を行う関数を$${\phi(x)}$$と置きます。
$${\phi(x)=(\phi_1(x), \phi_2(x), \phi_3(x)) = (x_1, x_2, sin(x_2\pi))}$$

この$${\phi(x)}$$は任意の数の$${\phi_i(x)}$$を持つことができます。どんな計算式で作ってもいいんですから。n個の$${\phi_i(x)}$$を持つ$${\phi(x)}$$による写像の結果はn次元になります。

例えば、$${x=(x_1, x_2)}$$の2次元だったとしても、それに$${\phi(x)=(x_1, x_1^2, x_1^3, x_1x_2, x_2)}$$を掛けると5次元になります。
$${(x_1,x_2)=(2,3)}$$なら、$${\phi(x)=(2,4,8,6,3)}$$という形で、$${x_1, x_2}$$の特微の性質が5個抽出されます

ということで特微抽出の話をしたのですけど、ここから「近さ」の話に入ります。

特微抽出後の複数次元ベクトル間の「近さ」は「類似度」と言い換えた方が個人的にイメージしやすいのでそう書きます。そして「類似度」はベクトル同士の内積で求められます。
$${\phi(x) \cdot \phi(x')=\phi_1(x) \cdot \phi_1(x') +\phi_2(x) \cdot \phi_2(x') +…+\phi_n(x) \cdot \phi_n(x')}$$

ここで、元のデータ$${x, x'}$$の類似度を比較するときは、$${x, x'}$$間の類似度よりも$${\phi(x), \phi(x')}$$の類似度を使う方が、データ間の比較に向いていそうです（さっきの三次元への写像でみたように）。

ここまでをまとめると、「近さ＝類似度」を定義するカーネル関数は、二つのデータをそれぞれ$${\phi(x)}$$で写像し、その内積を取ったものとおけます。式で言うと
$${k(x, x') = \phi(x) \cdot \phi(x')}$$

カーネル関数を適当に作ってみて射影関数について考える

長くなったので手を動かしてみます。

前回の「サンプルデータからそれを説明する関数をマッチする」作業を、天から降ってきた$${exp(-\beta(x^{(i)}-x)^2)}$$というゴツいガウスカーネルでなく、素朴な関数で実行してみます。

前回ガウスカーネルで計算した関数

素朴な関数はこんな感じ。
$${k(x, x') = \phi(x) \cdot \phi(x')}$$
$${ \phi(x) = x + x^2 + … + x^n}$$

コードはこうなる。

def simple_k_func(x1, x2, dim):
	return np.dot(np.array(phi(x1, dim)), np.array(phi(x2, dim)))

def phi(x, dim):
	return [x**(i+1) for i in range(dim)]

そして前回作ったKernelModelのfit関数の中で使うk_fincを書き換え。

def fit(self, x, y, l):
	self.x = x
	self.y = y
	self.k_func_ = lambda x1, x2: simple_k_func(x1, x2, dim=8) #here
	self.alpha_ = self._alpha(x, y, l)

で実行するとこんな感じになります。おぉ、ちゃんとフィットしている。

$${ \phi(x) = x + x^2 + … + x^n}$$のnを振ってみます。例えば$${dim=4}$$なら、$${\phi(x)=(x, x^2, x^3, x^4)}$$に射影した上でデータ間の類似度を$${k(x, x') = \phi(x)\phi(x') = xx'+x^2x'^2+x^3x'^3+x^4x'^4}$$と計算しています。

射影先の次元数をふってみた lambda=0.0001

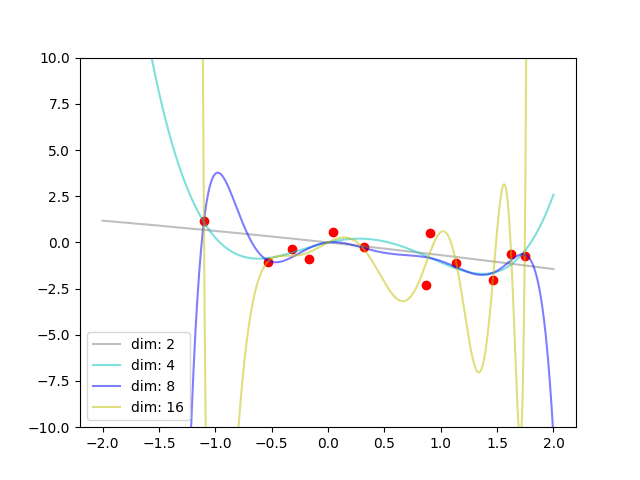
次元を増やすとフィット具合があがっています。これは考えてみれば当たり前な気がします。次元が増えると、よりうまくデータの違いを説明することが可能になるからです。特に、たまたま一番上の$${sin(x_2\pi)}$$のような切り分けの良い特徴抽出ができれば、各点との類似度を綺麗に定義できます。

ここまでをまとめると、「近さ＝類似度」を定義するカーネル関数は、二つのデータをそれぞれ$${\phi(x)}$$で写像し、その内積を取ったものとおけます。しかも$${\phi(x)}$$で射影する次元が多ければ多いほど正確に計算できる可能性があがりそうです。

射影関数の数を増やしたいけど・・・

んじゃ$${\phi(x)}$$で射影する次元を無限に増やせばいいね。と思うのですが、ここで問題があります。2つ(1)計算が大変。(2)どんな$${\phi(x)}$$がいいか分からない。

カーネル法の手順の最初には下記を計算する必要がありました。

$${K=\begin{pmatrix} k(x^{(1)},x^{(1)}) & k(x^{(2)},x^{(1)}) & ... & k(x^{(n)}, x^{(1)})\\k(x^{(1)},x^{(2)}) & k(x^{(2)},x^{(2)}) & ... & k(x^{(n)}, x^{(2)})\\ ... & ... & ... & ...\\k(x^{(1)},x^{(n)}) & k(x^{(2)},x^{(n)}) & ... & k(x^{(n)}, x^{(n)}) \end{pmatrix}}$$

ここで$${k(x^{(i)},x^{(j)})=\phi(x^{(i)})\phi(x^{(j)})=\phi_1(x^{(i)})\phi_1(x^{(j)})+\phi_2(x^{(i)})\phi_2(x^{(j)})+…\phi_n(x^{(i)})\phi_n(x^{(j)})}$$です。つまり、射影計算が2n回、内積計算がn回あります。つまり射影の数＝次元の数を増やすと、計算量が増えます。

$${k(x,x')}$$はサンプルデータ数の二乗回も計算する結構大変なやつです（$${K}$$作るために）。その一回の処理時間が伸びるのは嫌です。また、$${x^{(new)}}$$を使った予想のときの処理時間も伸びます。嫌です。

しかし一方で、「これが都合のよい$${\phi(x)}$$だ」とは簡単にわからないので、やたらめったら次元を増やしていくしかありません。困った。

ということで記事をまとめると、

  • カーネル関数$${k(x,x')}$$は、$${\phi(x)}$$によって高次元に飛ばした$${\phi(x), \phi(x')}$$の類似度＝内積とおける

  • $${\phi(x)}$$によって高次元に飛ばす際、その次元は高いほどサンプルデータ間の違いが明確になる＝予想が正確になる

  • しかし、次元を高くすると計算量が膨大になる問題がある

この次元に関する問題をどう対処するのか＝射影関数$${\phi(x)}$$をどう設定するか、が次の論点です。第二章も終わらん。
つぎはこちら

この記事が気に入ったらサポートをしてみませんか？