カーネル法の概要をゆるふわに掴む(1/2)
カーネル法がよくわからなかったので「カーネル多変量解析」を読み始めました。が、難しい……。
少しずつ読みながら、内容をpython使いながら噛み砕きつつ書いてみようと思います。線形代数苦手な人向け。どこか間違ってたらごめんなさい。
この記事では、第一章カーネル法概要を見てみます。二次元に点をランダムにマッピングして、それを通る近似曲線をカーネル法で求めてみます。
このシリーズの目次はこちら
この記事のゴール
サンプルデータを用意して、それらの点を通りそうなグニャグニャした$${f(x)}$$を求めるのがゴールです
サンプルデータはこんな感じです。横軸$${x}$$で縦軸$${y}$$。

ゴールのイメージはこんな感じ。
なお、サンプルデータのコードはこんな感じで作りました(pandasとかnumpyとかのインストールはしといてください)。data.pyとして保存して実行すると一番上の画像がでます。
import numpy as np
def random_point(num, seed=1):
np.random.seed(seed)
return np.random.randn(num, 2)
if __name__ == '__main__':
import matplotlib.pyplot as plt
x = random_point(12)
plt.scatter(x[:, 0], x[:, 1], c='red', marker='o')
plt.show()カーネルを使った近似曲線(理屈)
$${x}$$の値を入れたら、いい感じに$${y}$$の値が出てくるような近似曲線$${f(x)}$$を作りたいです。その近似曲線$${f(x)}$$を作るために、$${x^{(i)}}$$の入力のときは$${y^{(i)}}$$という結果だったよというサンプルデータの集まり($${i=1,2,…,n}$$)を使います。
近似曲線$${f(x)}$$は、$${x}$$の関数が幾つか足し合わされたものになりそうですね。$${x}$$が1つしかない$${y = ax +b}$$とかだと無理そうです。たぶん$${x}$$の多項式になるかなぁと予想します。
ここで突然ですが、変数$${x}$$とベクトル$${x^{(i)}}$$との近さを示す関数$${k(x^{(i)}, x)}$$があるとします(これをカーネル関数と呼びます。中身は後で)。この関数をサンプルデータ分だけ足してつなげてみます。例えばサンプルデータ3つなら
$${f(x) = a_1k(x^{(1)},x) + a_2k(x^{(2)},x) +a_3k(x^{(3)},x)}$$
各$${k}$$の影響度を調整するために重み$${a_i}$$を各$${k}$$に掛けています。文字がいっぱい出てきていますが、$${a_i}$$も$${x^{(i)}}$$も固定値なので、これの変数は$${x}$$だけです。
この考えを3個じゃなくてn個のサンプルデータとすると
$${f(x) = \sum a_i k(x^{(i)},x)}$$
この中の変数は$${x}$$だけかつn項もあり、しかも各データ点からの近さを使って計算するのだから、$${\alpha = a_1,a_2,...a_n}$$を適切に設定することで近似曲線$${f(x)}$$が得られそうな感じがします。
ということで、「どうやったらサンプルデータを使って$${\alpha = a_1,a_2,...a_n}$$を適切に設定できるか」が論点になります。
$${\alpha}$$を適切に設定すると、各$${x^{(i)}}$$を使って計算された予想値$${f(x^{(i)})}$$と実値$${y^{(i)}}$$の差が小さくなるはずです。
例えば$${x^{(1)}}$$を使ったとき、$${y^{(1)}}$$の予想値は
$${f(x^{(1)}) = a_1 k(x^{(1)}, x^{(1)}) + a_2k(x^{(2)},x^{(1)})+....+a_nk(x^{(n)},x^{(1)})}$$
です。実際の値との誤差は$${y^{(1)}-f(x^{(1)})}$$になります。
だから「すべてのサンプルデータに対して、誤差の二乗の合計が小さくなる$${\alpha = a_1,a_2,...a_n}$$が決められたら、よい近似曲線が書けた」といえます(二乗にしたのは誤差の正負を無視するため)。
誤差を一気に計算するため、すべてのサンプルデータの予想値を一気に計算する行列を考えます。ここで行列出てきちゃいますが、よくみると上の予想値の式を縦に並べただけです。
$${K=\begin{pmatrix} k(x^{(1)},x^{(1)}) & k(x^{(2)},x^{(1)}) & ... & k(x^{(n)}, x^{(1)})\\k(x^{(1)},x^{(2)}) & k(x^{(2)},x^{(2)}) & ... & k(x^{(n)}, x^{(2)})\\ ... & ... & ... & ...\\k(x^{(1)},x^{(n)}) & k(x^{(2)},x^{(n)}) & ... & k(x^{(n)}, x^{(n)}) \end{pmatrix}}$$
$${K\alpha=\begin{pmatrix} k(x^{(1)},x^{(1)}) & k(x^{(2)},x^{(1)}) & ... & k(x^{(n)}, x^{(1)})\\k(x^{(1)},x^{(2)}) & k(x^{(2)},x^{(2)}) & ... & k(x^{(n)}, x^{(2)})\\ ... & ... & ... & ...\\k(x^{(1)},x^{(n)}) & k(x^{(2)},x^{(n)}) & ... & k(x^{(n)}, x^{(n)}) \end{pmatrix}\begin{pmatrix} a_1 \\ a_2 \\ ...\\ a_n \end{pmatrix} = \begin{pmatrix} y^{(pred)}_1 \\ y^{(pred)}_2 \\ ...\\ y^{(pred)}_n \end{pmatrix}}$$
ので、誤差は$${(y-K\alpha)}$$、二乗した誤差の合計は$${(y-K\alpha)^T(y-K\alpha)}$$です。この誤差合計を最小にする$${\alpha}$$を見つけたいわけです。
$${\alpha}$$で偏微分と式変形すると以下が得られます(説明略)。
$${\alpha=K^{-1}y}$$
ここで、$${K}$$はカーネル関数$${k(x, x')}$$とサンプルデータ$${x^{(i)}(i=1,2,…,n)}$$があれば作れます。よって$${K^{-1}}$$も(正則なら)作れます。$${y}$$はサンプルデータの答えなので与えられています。よって$${\alpha}$$が求められてしまうのです。
カーネルを使った近似曲線(実装)
では、一番最初に表示したサンプルデータに対してカーネル法を実装してみます。基本上の理論をそのままコードにするだけ。
その前に。いままで棚上げになっていたカーネル関数$${k(x, x')}$$を下記とします。ガウスカーネルと呼ぶそうです。第一章の時点では詳細はわかりません。いったんこのまま計算します。
$${k(x, x') = exp(-\beta||x-x'||^2)}$$
$${\beta}$$は適当に決めるパラメータなので、$${k(x^{(i)}, x)}$$は$${x}$$だけを変数とする関数です。
これを頭のサンプルデータにあうように実装するとこんな感じ。
import numpy as np
def gaus(x1, x2, beta=1):
return np.exp(-1 * beta * ((x1 - x2) ** 2))上記をkernel_model.pyファイルの頭に書いて、この下にKernelModelクラスを実装していきます。
class KernelModel():
def fit(self, x, y):
pass
def predict(self, x):
passfit関数はn個のサンプルデータ$${x^{(1)}, x^{(2)},….,x^{(n)}}$$と$${y^{(1)}, y^{(2)},….,y^{(n)})}$$を受けて、$${\alpha}$$を計算し、近次関数$${f(x)}$$を作ります。一方、predict関数は予想したい$${x'}$$を受けて、予想値$${y'}$$を返します。
fit関数で$${\alpha}$$を計算するには、まず$${K}$$を計算します。この例ではサンプルデータが12個なので、カーネル関数を12 x 12回計算して$${K}$$を作ります。
#KernelModel内
def _K(self, x):
dim = len(x)
matrix = []
for i in range(dim):
for j in range(dim):
matrix.append(self.k_func_(x[j], x[i]))
matrix = np.array(matrix)
matrix = matrix.reshape(dim, -1)
return matrix$${\alpha}$$は$${\alpha=K^{-1}y}$$なので、
#KernelModel内
def _alpha(self, x, y):
k = self._K(x)
return np.linalg.inv(k).dot(y)fit関数はこれで終わりです。
#KernelModel内
def fit(self, x, y):
self.x = x
self.k_func_ = lambda x1, x2: gaus(x1, x2, beta=1)
self.alpha_ = self._alpha(x, y)xをself.xに保存しているのはpredictでも使うため。predictは求めていた$${f(x)}$$です。xを与えると、そのxと各サンプルデータの近さ$${k(x^{(i)}, x)}$$に重み$${a_i}$$を掛けて足し合わせることで$${y}$$を導きます。
#KernelModel内
def predict(self, x):
pred_y = 0
for i in range(len(self.x)):
pred_y += self.alpha_[i] * self.k_func_(self.x[i], x)
return pred_yつまり全体像はこんな感じ。
import numpy as np
def gaus(x1, x2, beta=1):
return np.exp(-1 * beta * ((x1 - x2) ** 2))
class KernelModel():
def fit(self, x, y):
self.x = x
self.k_func_ = lambda x1, x2: gaus(x1, x2, beta=1)
self.alpha_ = self._alpha(x, y)
def predict(self, x):
pred_y = 0
for i in range(len(self.x)):
pred_y += self.alpha_[i] * self.k_func_(self.x[i], x)
return pred_y
def _alpha(self, x, y):
k = self._K(x)
return np.linalg.inv(k).dot(y)
def _K(self, x):
dim = len(x)
matrix = []
for i in range(dim):
for j in range(dim):
matrix.append(self.k_func_(x[j], x[i]))
matrix = np.array(matrix)
matrix = matrix.reshape(dim, -1)
return matrix試しに以下を実行すると、結構正解しています($${f(x^{(1)})}$$の予想値を計算して、$${y^{(1)}}$$と比較している)。
import data
d = data.random_point(12)
x = d[:, 0]
y = d[:, 1]
m = KernelModel()
m.fit(x, y)
print("real: ", x[0], " predict: ", m.predict(x[0]))real: -0.6117564136500754 predict: -0.6117560863494873結果
このpredict関数を表示してみましょう。

全ての点を通るように関数が作成されています。きれい。コードはこんな感じ。devideの数だけ$${(x, f(x))}$$を計算して並べてます。
import kernel_model
import data
import numpy as np
import matplotlib.pyplot as plt
d = data.random_point(12)
model = kernel_model.KernelModel()
model.fit(x=d[:, 0], y=d[:, 1])
x_min = -2
x_max = 2
devide = 500
p = np.linspace(x_min, x_max, devide)
plt.plot(p, [model.predict(p[k]) for k in range(devide)])
plt.scatter(d[:, 0], d[:, 1], c='red', marker='o')
plt.ylim(-10, 10)
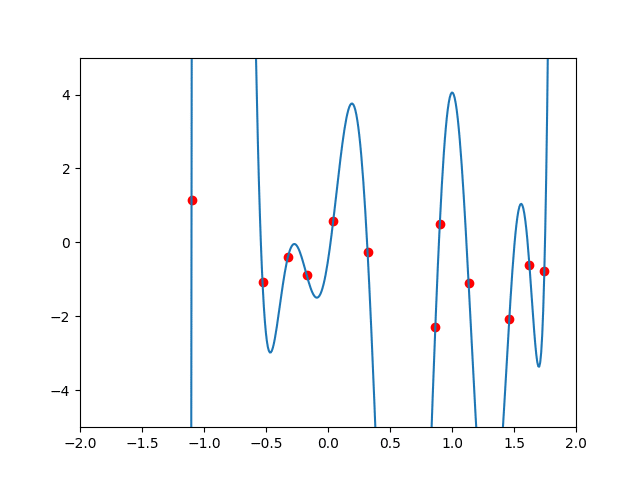
plt.show()ただ、この結果、過学習っぽいです。表示範囲伸ばしてみるとこんな感じ。他の点を予想しようとすると使えなさそうですね。

$${f(x)}$$がサンプルデータに合うように複雑な関数になりすぎているのです。この問題を解消するために、サンプルデータずばりは通らないけど、かなり近くを通るし自然な感じの$${f(x)}$$を作ります。
長くなったので、いったんここまで。次はその関数を作って、関数のパラメータをいじったりします。まだ第一章が終わらない……。
続き:https://note.com/tanuki_112/n/n233008df0639
ちなみにpythonのコード書きながら機械学習学ぶならこれがおすすめ。「カーネル多変量解析」にはコードはないので。
この記事が気に入ったらサポートをしてみませんか?
