
投資は確率論では語れません
ちょっと前のものですが、下の日経の記事が目に止まりました。積み立て投資を確率モデルを用いてシミュレーションすると、20年以上の長期であって積み立てた元本を下回るリスクがあるとし、金融庁のサイトで提供されている資産運用シミュレーションが示すように、右肩上がりで増えるものでは無いですよ、と警鐘を鳴らしています。
その金融庁のサイトの資産運用シミュレーションでは、運用利回り5.24%(記事の分析で用いられている値)で毎月1万円を20年間積み立てるとすると、以下のような結果が表示されます。
記事では、積み立て投資の対象となる株や債券などを組み込んだ投資信託には価格変動リスクがあるので、金融庁のシミュレーション結果が示すように、右肩上がりで資産が増える訳ではない、と指摘しています。
それは、ごもっともなことなのですが、、、、、

モンテカルロシミュレーションによる運用成果の分布
記事では、ここで金融工学の知恵を借りて(というところが既に胡散臭いが)、積み立て投資の運用成果のシミュレーションを行っています。このシミュレーションとは、モンテカルロシミュレーションといって、将来の価格変動シナリオを乱数を用いて1万通り作り、それぞれのシナリオでの運用成果をまとめて分布を求めるものです。
下の表はその結果をまとめたものです。これに基づいて、「積み立て投資の落とし穴」として、総平均の結果(表の一番右側)を例にとって以下の点を指摘しています。
(1)平均リターン(5.24%)で運用した場合の成果は、平均値(20年で416万円)で表されますが、これは運用が極端にうまく行ったケースの影響を受けているもので、シミュレーション結果による分布の中央値(20年で386万円)と最頻値(20年で370万円)は平均値を下回っていると指摘しています。つまり、金融庁のサイトのシミュレーションで平均リターンに基づく運用成果には、届かない可能性の方が高い、と説明しています。
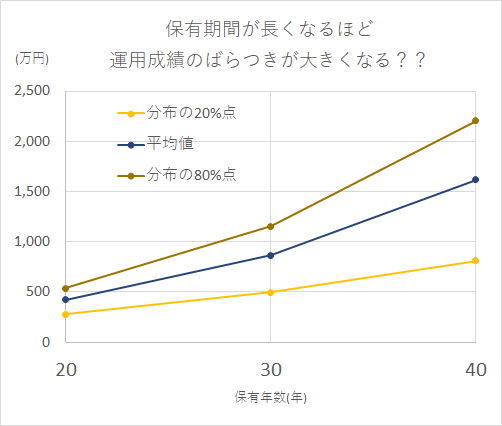
(2)投資元本を下回る確率は、20年で9.2%、30年で5.2%、40年で3.1%と投資期間が長くなると元本割れのリスクは小さくなっていきますが、投資成果のばらつき(20/80倍率)は大きくなっています。したがって、「長期投資はリスクを減らす」ということはない、言っています。

単純な確率モデルを長期の価格変動に使うことの問題
このモンテカルロシミュレーションで用いられている価格変動モデルは、ランダムウォークといって、価格がランダムに変動するという前提ですが、ランダムウォークは長期的な価格変動をモデル化することには必ずしも向いていないと思います。
なぜなら、株式、あるいは株式を組み込んだ投資信託の価格は、投資対象の企業価値と本来連動するものであって、仮にそれが短期的な投機や需給の要因などによって、企業価値から大きく乖離すれば、本来あるべき水準に戻る力(これを価格の平均回帰性と呼びます)が働き、長期的には価格が企業価値の成長率に沿って上昇することが期待されるからです。
したがって、下のグラフが示すように、保有年数が長くなるほど、平均値からの乖離が拡大してゆくようなモデルは、ちょっとおかしいのではないかと思います。
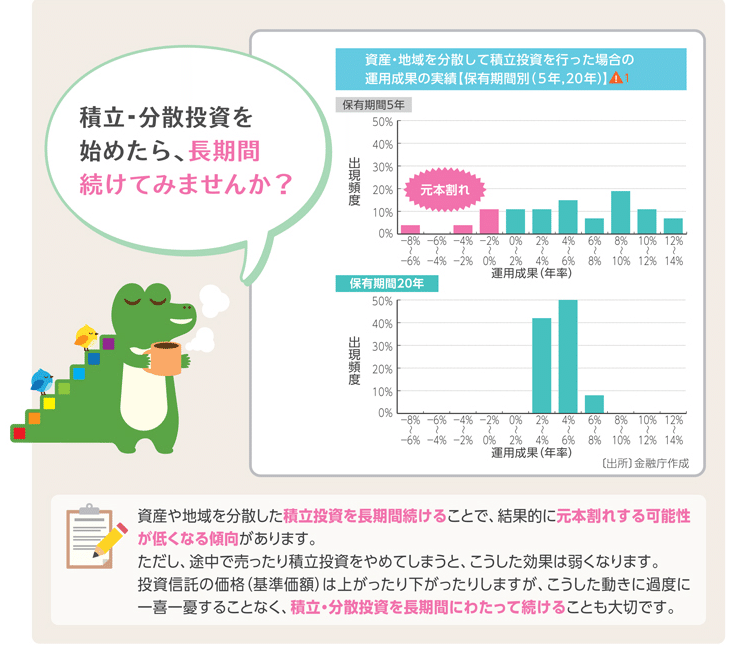
また、下の図は、金融庁の「つみたてNISA早わかりガイドブック」から引用したもので、実際の価格データを使って積み立て投資をシミュレーションしています。
ご覧の通り、保有期間が5年より20年の方が、バラツキが小さくなっていて、確率モデルの結果とは反対です。確率モデルが、長期における実際の価格変動をうまくモデル化できていない証拠ではないでしょうか。
下のグラフは、投資期間20年(240月)における、1万通りのシミュレーションの1つを取り出してみたものです。このケースでは、価格が13年(160月)目くらいまでは、10,000と12,000の間で推移していて、その後、下落に転じて20年後には、当初の半分の5,000程になってしまい、資産総額は積み立て元本(240万円)を大きく下回る139万円になってしまいます。
しかし、株価指数が20年後に半分になってしまうことってあるのでしょうか。世界の人口はまだまだ増加し続け、消費が増え経済が成長していく中で、どのようにしたら株価が7年にも渡って下落し続けることができるのでしょう。
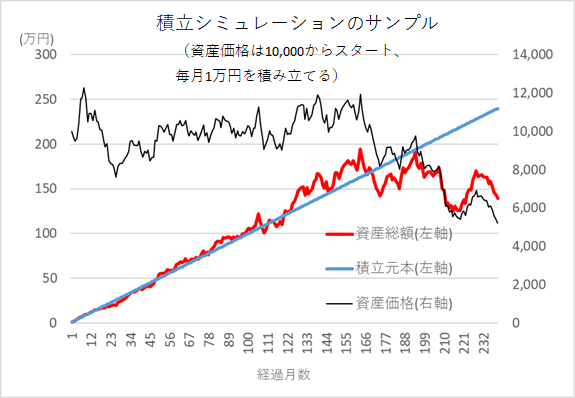
ここでも、単純な確率モデルでは長期の経済成長を前提とした株価の変動をうまく表されていないことがうかがえます。
さらには、分布の形状を決めるファクターである平均リスクは、過去5年間のデータに基づいて13.77%と決めていますが、これも過去3年とか10年のデータにすれば平均リスクの値も変わり、この記事が示している「理論的な分布」は全く異なるものになるかもしれません。
投資において重要なのはその哲学
最後に、記事は以下の文章で締めくくられています。
ブラックスワン現象などを念頭に、「理論上の分布よりも下振れするリスクがある」と指摘する専門家がいることも付記しておく。
「ブラックスワン」という言葉は、世の中何が起こるか分からないということを想起させ、長期投資のリスクを過大に見せる効果があります。結局この記事は、積み立て投資を始めようとしている人、あるいは既に始めている人に対して、必要以上に不安を感じさせることを目的としているとしか思えません。
私はブラックスワンを引用している記事や解説は信用しません!
一般生活者の皆さんには、このような情報に惑わされずに、積み立て投資を続けて欲しいと思います。
また、投資において重要なのは、今回の記事のような確率モデルを使った分析(もどき)よりも、その哲学を理解するところにあると思います。
その点については、以前書いたこちらのnoteをご覧いただければと思います。
この記事が気に入ったらサポートをしてみませんか?
