基礎編３２　「分子を求めるテクニック④」【研究】並べて２けたの数をつくって３の倍数

　右の図のように，１，２，３，４の数字が１つずつ書かれた４個の玉が入った袋がある。この袋の中から玉を１個取り出し，玉に書かれた数字を確認してもとに戻す。これを２回行い，１回目に確認した数字を十の位とし，２回目に確認した数字を一の位として２けたの整数をつくる。このとき，その整数が３の倍数である確率を求めよ。ただし，この袋からどの玉が取り出されることも同様に確からしいものとする。（高知県2011）

問題を解く前に・・・

　基礎編最後の研究問題は「定番」と言っていいほど、あちこちで出される問題です。例題のように「２けたの数をつくったときに、３の倍数である確率を求める」のですが、書いてあるとおりに真面目に２けたの数をつくって、３の倍数であるかどうか３でわってみて・・・としなくても、実は３の倍数判定方法を知っていると、パッと早く解けるパターンの問題です。

　それは各けたの数の和が３の倍数なら、もとの数は３の倍数（各けたの数の和が３でわり切れれば、もとの数も３でわり切れる）というルールです。

　この問題を出題ということは、「このルールを知ってるかな？　知ってたら速く解けるって思いつくかな？」と出題者は考えているはずです。数学マニアをくすぐる問題として「定番化」しているような気がします。

※2020島根県、2018三重県・岡山県・長崎県、2017島根県、2016福島県・和歌山県・熊本県、2015鳥取県、2014富山県、他私立学校多数

分母は・・・

　４つの玉から１つ取り出して、戻してもう１つを取り出す
→偶然２つで表　→表はいじらない

分母は１６

分子は・・・

　問題文にあるように２けたの数をつくって

３でわり切れるか確認をしてもいいですが・・・・

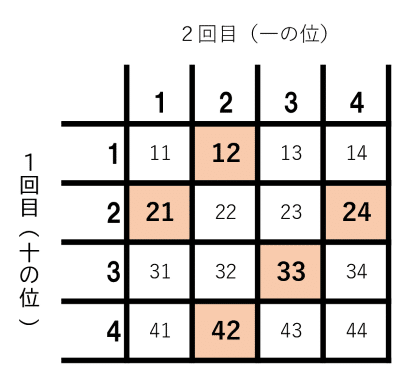
「３の倍数←→各けたの数の和が３の倍数」を利用したほうが、簡単に終わります。和が３の倍数になる組合せは表の中の○印の５通りのみ。

分子は５

答えは・・・

答　　　５／１６

　（約分できないのでこれでおしまい）

問題を解いた後で・・・

　なぜ「各位の数の和が３の倍数→もとの数が３の倍数」なのか、文字を使って証明する問題も押さえておいた方がいいと思いますが、もう少し簡単に説明もできると思います。動画として、

を貼っておきます。

…というわけで、基礎編おしまい。

　以上３５問で、基礎編はおしまいです。中学校の確率のシンプルな問題はこれで解けるようになっています。（いるはずです）
　しかし，確率のからんだ入試問題がこれで完璧かというと，そうはいかないのです。ここから先、このnoteでは、大きく、別の数学の知識・技能が必要な《融合問題》と、数学の知識ではなく問題分に示されている別の装置の操作が必要な〈応用問題〉の２つに分類して，紹介していくことにします。

－－－－－－－－－－－－－－－－－－－－－－－
＜前の問題　　　　　　　　　　
問題一覧