
沖縄県|公立高校入試確率問題2015
袋Aには1から4の数字が1つずつ書かれた4個の球が入っており,袋Bには1から6の数字が1つずつ書かれた6個の球が入っている。A,Bの袋から,それぞれ1個ずつ球を取り出し,球の番号を確認する。
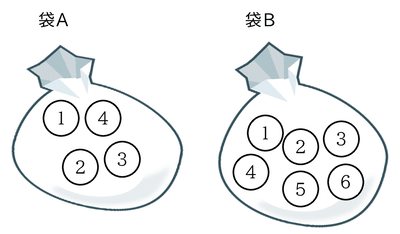
このとき,次の各問いに答えなさい。
ただし,袋A,Bの中は見えないものとし,球の取り出し方は,それぞれ同様に確からしいものとする。
問1 球の取り出し方は全部で何通りあるか求めなさい。
問2 次に,袋Aから取り出した球の番号を$${x}$$,袋Bから取り出した球の番号を$${y}$$とし,その$${x}$$,$${y}$$の値の組を座標とする点Pについて考える。例えば,袋Aから取り出した球の番号が1,袋Bから取り出した球の番号が2の場合は,点(1,2)を表すものとする。
このとき,次の(1),(2)に答えなさい。
(1)点Pと原点との距離が5となるのは全部で何通りあるか求めなさい。
(2)点Pと原点との距離が5以上となる確率を求めなさい。

分類:融合《D2》座標平面上の図形-2点の距離
起こりうるすべての場合は
偶然は2つ起こりますので表で考えることにしましょう。袋Aで起こる偶然と袋Bで起こる偶然は、お互いに影響をしませんので、表はこのままになります。

ですから、起こりうるすべての場合は表のマス目の総数24通りで、その場合が起こることも同様に起こることが確からしいです。
問2のアプローチ1 計算する
(1)は表で$${x^2+y^2}$$を計算して、ちょうど25になるところ、(2)は25以上になるところを数えればよいです。
問1でつくった表の各マスに$${x^2+y^2}$$を書き入れます。なお、$${y}$$=5と$${y}$$=6のときは$${x^2+y^2}$$は必ず25より大きくなりますので、特に計算しなくてもよいでしょう。
というわけで、(1)は表の〇印の点(3,4)と点(4,3)の2通り、(2)は表の〇印と✔印のあわせて11通りですので、求める確率は$${\bm{\dfrac{11}{24}}}$$。

アプローチ2 座標平面にコンパスで
点Pと原点との距離が5となるのは・・・と思ったら、作図のためにコンパスがあるではありませんか。問題用紙の座標平面上に、コンパスで原点を中心とする半径5の円をかいてしまいましょう。

ちょうど距離が5になるのは点(3,4)と点(4,3)の2通り。5以上となるのは印をつけた11通りですから、確率は$${\bm{\dfrac{11}{24}}}$$と求めることができます。
コンパスで考えるときは、念のために計算で誤差がないかどうか、確認をしておきましょうね。
答
問1 24通り
問2 (1) 2通り (2) $${\dfrac{11}{24}}$$
この記事が気に入ったらサポートをしてみませんか?
