長崎県Ｂ問題｜公立高校入試確率問題2020

　長崎県はＡ問題とＢ問題があり、学校で選んで出題されていました。（２０２２年現在は、１つの問題で実施）

　大小２つのさいころを同時に１回投げる。ただし，それぞれのさいころの目は１から６まであり，どの目が出ることも同様に確からしいとする。このとき，次の(１)，(２)に答えよ。

(１)　大小２つのさいころの出る目の数が同じになる確率を求めよ。

(２)　右の図のような正六角形ＡＢＣＤＥＦがある。大小２つのさいころを同時に投げ，１の目が出たら点Ａ，２の目が出たら点Ｂ，３の目が出たら点Ｃ，４の目が出たら点Ｄ，５の目が出たら点Ｅ，６の目が出たら点Ｆをそれぞれ選ぶ。選んだ２点と点Ａを頂点とする三角形を作りたい。例えば，２，３の目が出たら△ＡＢＣができ，１，２の目が出たら三角形はできない。このとき，次の(ア)，(イ)に答えよ。
　　(ア)　三角形ができない確率を求めよ。
　　(イ)　直角三角形ができる確率を求めよ。

（１）は・・・

　基礎編３で同じ問題を解説していますのでリンクだけ貼っておきます。答えは$${\dfrac{6}{36}=\bm{\dfrac{1}{6}}}$$

（２）は

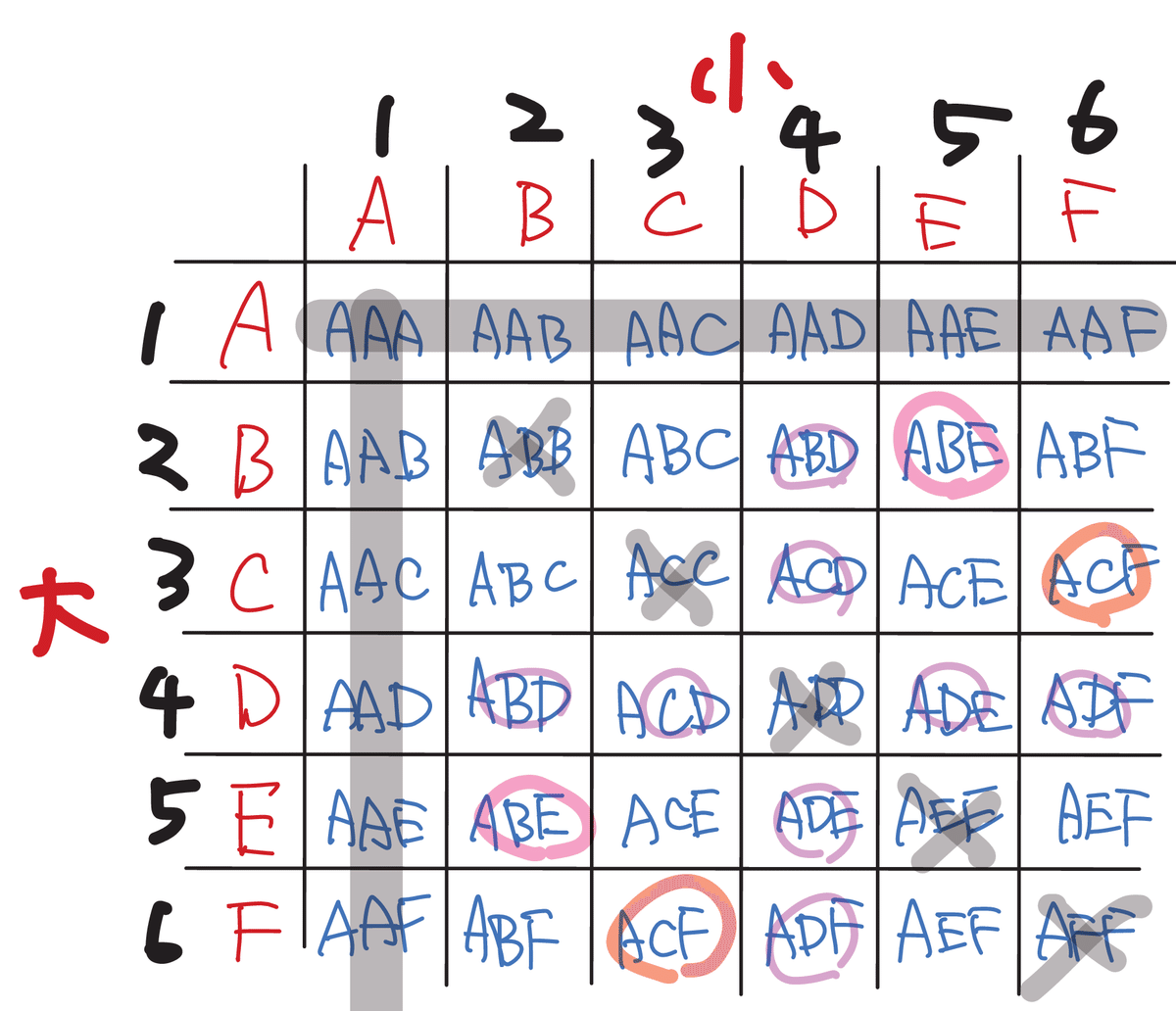
　それぞれのさいころで出た目によって選んだ２点と点Ａの３つの点について、それぞれ表のマスに書き入れておきましょう。

（ア）

　三角形ができないのは、３つの点がそれぞれ別々でない場合、灰色で印をつけた１６通りなので、求める確率は$${\dfrac{16}{36}=\bm{\dfrac{4}{9}}}$$

（イ）

直角三角形ができるのは、３つのうち２点が「まむかい」（もう少し数学的に正確に説明すると、正六角形ABCDEFを内接する円をかいたときに、円周角の性質より、その円の直径になる辺を含む三角形になるとき）です。
　つまり、Ａ・ＤかＢ・ＥかＣ・Ｆを含んで、三角形になる場合を探せばよいですので、表の１２通りということになり、その確率は$${\dfrac{12}{36}=\bm{\dfrac{1}{3}}}$$と求めることができます。

Ｂ問題　答

（１）　$${\bm{\dfrac{１}{６}}}$$
（２）（ア）$${\bm{\dfrac{４}{９}}}$$　　　（イ）　$${\bm{\dfrac{１}{３}}}$$

分類：

　（１）基礎編３

　（２）（ア）　融合問題B1中１・２図形範囲

（イ）　融合問題B2円周角