
島根県|公立高校入試確率問題2016
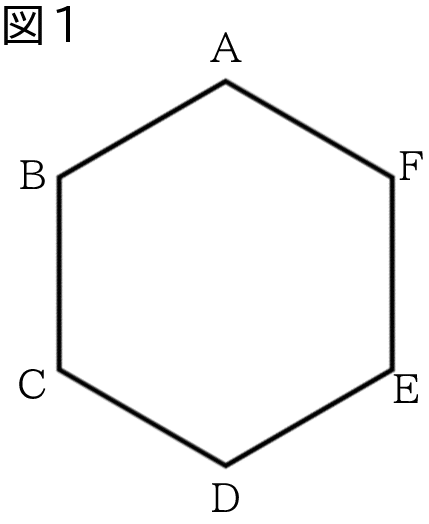
図1のような正六角形ABCDEFがある。下の1,2に答えなさい。
1 1つのサイコロを投げて出た目に対応する正六角形の頂点に点Pを置くこととする。ただし。サイコロの目と頂点との対応は表のとおりである。例えば,サイコロの出た目が1であるとき,対応する頂点はAである。

次の(1)(2)に答えなさい。
(1) 3点A,B,Pを結んだとき,三角形ができる確率を求めなさい。
(2) △ABPが直角三角形となるのは点Pがどの頂点にあるときか。そのような頂点をすべて求め,A~Fで答えなさい。
2 大小2つのサイコロを同時に投げ,大のサイコロを投げて出た目に対応する正六角形の頂点に点Pを,小のサイコロを投げて出た目に対応する正六角形の頂点に点Qを置くこととする。ただし,それぞれのサイコロの目と頂点との対応は1の表と同じである。
このとき,△APQが直角三角形となる確率を求めなさい。
分類:融合《B2》円周角
(1)三角形ができるということは・・・?
つまり、PがAかB以外の点であればよいわけですから、CかDかEかFのどれかであればよくて、3~6の4つの目のどれかが出ればよいわけです。起こりうるすべての場合は6通りで、そのどれが起こることも同様に確からしいですから、求める確率は$${\dfrac{4}{6}=\bm{\dfrac{2}{3}}}$$。
(2)3点を結ぶと直角三角形、ということは
正六角形ということは、6つの頂点は1つの円の円周上にあります。
円周角の問題として考えると、円周上の3点を結ぶと直角三角形になるということは、3点のうちの2点が中心をとおる直径になっていればよいのです。Aと結ぶと直径になるのはD、Bと結ぶと直径になるのはEですから、求めるのはこの2点がすべて、ということになります。
2はどうしましょう。
1の(2)が上手に誘導してくれているので、△APQが直角三角形になるということは、
(1)APが直径(つまり点Pは点D)
(2)AQが直径(つまり点Qは点D)
(3)PQが直径
のどれかであればよい、ということに気づくとよいわけです。ただし、
(甲)P・QのどちらかがA
(乙)P・Qが同一の点
となってしまってはそもそも三角形にはなりませんので、除外しなければなりません。
2つのさいころを投げますので、まずは表をかいて、あとは条件を満たすものにチェックをしましょう。

起こりうるすべての場合は36通りで、そのいずれが起こることも同様に確からしいです。そのうち、条件に当てはまるのが12通りですので、求める確率は$${\dfrac{12}{36}=\bm{\dfrac{1}{3}}}$$
答
1 (1) $${\bm{\dfrac{2}{3}}}$$ (2)D,E 2 $${\bm{\dfrac{1}{3}}}$$
この記事が気に入ったらサポートをしてみませんか?
