
山口県|公立高校入試確率問題2011
図のように,紙にかいた正五角形ABCDEと,白石,黒石が1個ずつある。
次の操作を行うとき,下の(1),(2)に答えなさい。
なお,操作で用いる大小2つのさいころは,それぞれ1から6までの目が出るものとし,どの目が出ることも同様に確からしいものとする。

操作
① 白石,黒石を頂点Aに置く。
② 大小2つのさいころを同時に1回投げ,大きいさいころの出た目の数を$${a}$$,小さいさいころの出た目の数を$${b}$$とする。
③ 白石を,左回りに$${a}$$の数だけ頂点を順に移動させる。
④ 黒石を,右回りに$${b}$$の数だけ頂点を順に移動させる。
(1) 次の文の[ア],[イ]にあてはまる記号を入れなさい。
操作の①を行い,操作の②で$${a}$$の数が6,$${b}$$の数が3であった。操作の④まで終えたとき,白石は頂点[ア]に,黒石は頂点[イ]に止まっている。
(2) 操作の①から④まで終えたとき,白石,黒石が同じ頂点に止まっている確率を求めなさい。
分類:応用編〈2〉 動かす② 循環型
表にまとめてみましょう。
さいころ2つなので表を書くことにします。そして、それぞれのさいころの目によって、白石と黒石がどの頂点の位置にあるか、書き添えておくことにしましょう。
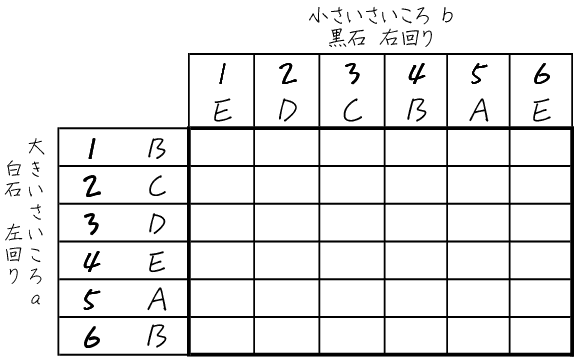
(1)は、$${a}$$=6のときはB、$${b}$$=3のときはCということです。
(2)は、同じ位置にあるところに印をつけることにしましょう。

しるしは7つ、全ての場合は36通りですので、求める確率は$${\bm{\dfrac{7}{36}}}$$
答
(1) ア B イ C (2)$${\bm{\dfrac{7}{36}}}$$
この記事が気に入ったらサポートをしてみませんか?
