
岐阜県|公立高校入試確率問題2024
右の図のような正三角形ABCがあり,点Pは頂点Aの位置にある。また,0から4までの数字が1つずつ書かれた5枚のカード[0] [1] [2] [3] [4]が,袋の中に入っている。
次の操作を2回行う。
【操作】
袋からカードを1枚取り出し,そのカードに書かれた数字の回数だけ,Pを正三角形の頂点から頂点へ左回りに移動させる。Pを移動させた後,取り出したカードを袋に戻す。

例えば,1回目に[2]のカードを,2回目に[0]のカードを取り出したとき,1回目の操作後にPは頂点Cにあり,2回目の操作後もPは頂点Cにある。
次の(1)~(3)の問いに答えなさい。
(1) 1回目の操作後にPが頂点Aにある確率を求めなさい。
(2) 1回目の操作後にPが頂点Aにあり,2回目の操作後もPが頂点Aにある確率を求めなさい。
(3) 2回目の操作後にPが点Aにある確率を求めなさい。
分類:応用❷(他のものを動かす、循環型)
(1)は操作の確認
まず確認ですが,「そのカードに書かれた数字の回数だけ,Pを正三角形の頂点から頂点へ左回りに移動させる」ということなので,[0]のカードを取り出したときは[0回左回りに移動」ということなので,結局そのまま,と考えてよさそうですが、はたして正しい考え方でしょうか?
例えば,1回目に[2]のカードを,2回目に[0]のカードを取り出したとき,1回目の操作後にPは頂点Cにあり,2回目の操作後もPは頂点Cにある。
とあり,あっていますね。ですから,それぞれのカードを出したとき,Pは
[0]→A
[1]→B
[2]→C
[3]→A
[4]→B
の位置にあります。問われている1回目の操作後にPが頂点Aにある場合は[0]と[3]をひいたときの2通り。確率は,$${\dfrac{2}{5}}$$となります。
(2)2回操作するので表で考えましょう
2回操作をするので,表で考えるといいですね。

操作が終わった後,取り出したカードは袋に戻しますので,[0]→[0]のような取り出し方も可能です。ですから,表はこのままになります。
1回目終わったタイミングで,Pがどの位置にいるかをかいておいて,2回目の目でどこに移動するかを,各マスに書いておくことにします。。

(2)で考えるのは,1回目の操作後にPが頂点Aにあり,2回目の操作後もPが頂点Aにある場合についてですから,

この行のうちのAの場所ですから,

当てはまるのはこの4通り。起こりうるすべての場合の数は25通りですから,求める確率は$${\dfrac{4}{25}}$$。
(3)さっきの表で考えましょう
すでに表はできていますから,2回目でPが頂点Aに移動している場合を数えると,
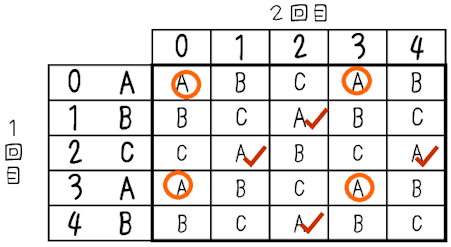
8通りですね。求める確率は$${\dfrac{8}{25}}$$。
答
(1)$${\bm{\dfrac{2}{5}}}$$ (2)$${\bm{\dfrac{4}{25}}}$$ (3)$${\bm{\dfrac{8}{25}}}$$
問題を解いた後に
「何回移動したか」を頂点に対応させて考えると
0回 → A
1回 → B
2回 → C
3回 → A
4回 → B
5回 → C
6回 → A
7回 → B
8回 → C
なので,それぞれの数字の和を表のマス目に書き入れて,0,3,6になる場合を数える,という方針でもよいですね。

この記事が気に入ったらサポートをしてみませんか?
