福井県｜公立高校入試確率問題2020

　図１のように，箱にはＢ，Ｃ，Ｄ，Ｅ，Ｆの文字が書かれたカードが１枚ずつ入っている。この箱からカードを１枚取り出し，文字を記録してから，カードを箱に戻す。これを２回繰り返すとき，次の問いに答えよ。ただし，箱からのカードの取り出し方は同様に確からしいものとする。（Ａ問題・Ｂ問題共通）

（１）　記録した２つの文字が同じものである確率を求めよ。

（２）　図２のように，正三角形ＡＢＣの各辺の中点をＤ，Ｅ，Ｆとする。点Ａと，記録した２つの文字と同じ点をすべて結んでできる図形が三角形となる確率を求めよ。
　例えば，１回目にＣ，２回目にＦを記録したとき，この図形は３点Ａ，Ｃ，Ｆを頂点とする三角形となる。１回目も２回目もＦを記録したとき，
この図形は２点Ａ，Ｆを結んだ線分となる。

分類：（１）１３　取り出して，戻してもう１回
　　　（２）融合《B1》中１・中２図形範囲

（１）は表をかきます。

　１回目は〔Ｂが記録されること〕，〔Ｃが記録されること〕，〔Ｄが記録されること〕，〔Ｅが記録されること〕が同様に確からしいことがら，そして、いったんもどしますから２回目もそれぞれについて〔Ｂが記録されること〕，〔Ｃが記録されること〕，〔Ｄが記録されること〕，〔Ｅが記録されること〕が起こることも同様に確からしいです。表をかいて考えると下のようになります。すべての起こりうることがらは２５通りで、そのいずれもどのように確からしいです。

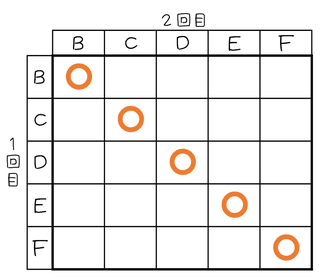
　そのうち記録した２つの文字が同じものである場合は、上の５通りですから、その確率を求めると$${\dfrac{5}{25}=\bm{\dfrac{1}{5}}}$$

（２）はこちら

（２）の問題は「融合問題編《Ｂ１》」の例題２として採録しているので、解説はそちらをご覧ください。

答

（１）　$${\bm{\dfrac{1}{5}}}$$　　（２）　$${\bm{\dfrac{16}{25}}}$$