
広島県|公立高校入試確率問題2017
右の図のように、∠ABC=90°である直角二等辺三角形ABCと長方形ADEBがあります。辺BEの中点をPとすると,AB=BFです。また、文字を書いた5枚のカード,B,C,D,E,Fが袋の中に入っています。この袋の中から2枚のカードを同時に取り出します。このとき,それらのカードと同じ文字の点と点Aの3点を頂点とする三角形が,直角三角形になる確率を求めなさい。

分類:融合《B1》 中1・中2図形範囲
図形は結局どういうことか?

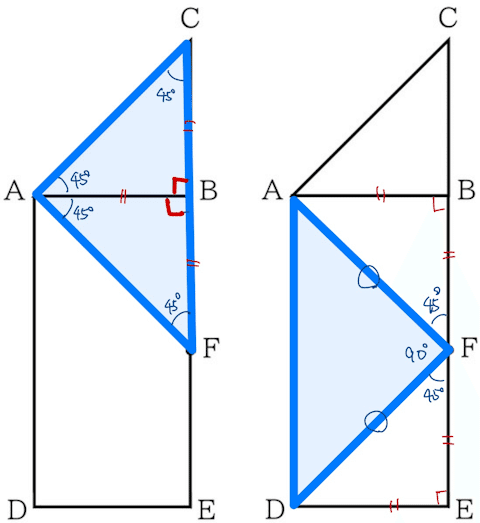
問題文の条件を整理すると、次の図のようになります。AB=AC=DE=BF=EFで、AD=2ABですね。
で、カード2枚をひいたとき、起こりうる組み合わせは、次の表のように10通りです。2枚のカードを同時に取り出しますので、順番は関係ないC型ですね。

さて、出てきたカードをもとに三角形をつくったときに直角三角形になるのは、そのうちの7通りです。

特に△ACFと△ADFが直角三角形になる、ということがつかめるかどうかがこの問題のポイントになりそうです。
起こりうる場合は全部で10通りで、そのうち条件に当てはまるのは7通りですので、

その確率は$${\bm{\dfrac{7}{10}}}$$
答
$${\bm{\dfrac{7}{10}}}$$
問題を解いた後に
「取り出す問題」は、「確率のかけ算」で解けてしまう問題が結構あって、その解き方だけで説明をされてしまうことが往々にしてあるのですが、このように図表ですべての場合をあげて、それぞれについて条件に合っているかどうかチェックする考え方が、中学数学では大切ですよ、といういい融合問題です。そして、△ACFと△ADFが直角三角形になるかどうかを判定できるかどうか、というのが、問題をよく練って出題している感じを受けます。図形の問題として見ても、いい問題。
この記事が気に入ったらサポートをしてみませんか?
