
三角関数を用いてアニメーションを作る
またある日の朝、二匹の猫が家の中から外を見ています。
どうやら、今日はあいにくの雨みたいです。
ミケ:はぁ~、今日は雨みたいだね。
マロ:だねぇ~。
ミケ:いつもだったら外で走り回れるのに、今日はなんもできないや。
マロ:たまにはゆっくりするのもいいんじゃない?
ミケ:確かにいいかも。 じゃあのんびり行きますか~。
マロ:で、なにする?
ミケ:え?ゆっくりするんじゃ…?
マロ:ずっとゴロゴロしてるのも飽きちゃうでしょ? なんかしようよ!
ミケ:う~ん、そうだなぁ…。 そうだ、"あれ"をやってみようか。
マロ:"あれ"? "あれ"って何?
ミケ:ん~とね、三角関数は分かるよね?
マロ:もちろん! 馬鹿にしてる?
ミケ:いや、馬鹿にするつもりはないんだけど…(汗) まぁ今回はその三角関数をテーマにしようと思って。
マロ:え、でもそれじゃあ僕がやったほうがよくない?
ミケ:普通はそう思うでしょ? でもね、ただ三角関数を学ぶってわけじゃないんだよ。
マロ:…というと?
ミケ:いままでのプログラミングは、画面が真っ黒でなんか退屈だったよね?
マロ:うん! ってことは...、もしかして!?
ミケ:そう!そこでウィンドウアプリケーション的なのを作っていこうか。
マロ:おお! でも三角関数と何の関係があるの?
ミケ:よくぞ聞いてくれました! 今回はね、ウィンドウに三角関数を使ったアニメーションを表示させてみようと思うよ!
マロ:おぉ~、これであの真っ黒な画面からおさらばできる!!
ミケ:さて、じゃあ準備していこうか!
どうやら今回は、三角関数を使ったアニメーションを作っていくようです。
三角関数の基礎知識
ミケ:とりあえず三角関数の復習からしたいんだけど、ここはマロにお願いしていいかな?
マロ:いいよ~、まかせて!
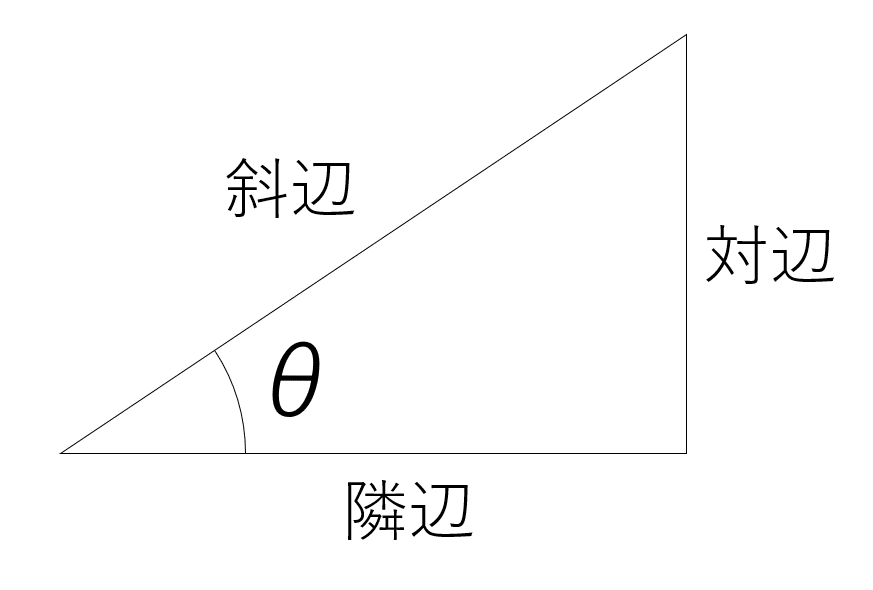
とりあえずそれぞれの辺はこの画像のとおりに呼ぶね。
そしてお待ちかねの三角関数とは、
$${sinθ = \frac{斜辺}{対辺}}$$
$${cosθ = \frac{斜辺}{隣辺}}$$
$${tanθ = \frac{隣辺}{対辺}}$$
で定義されるものである。例えば30度の時は、
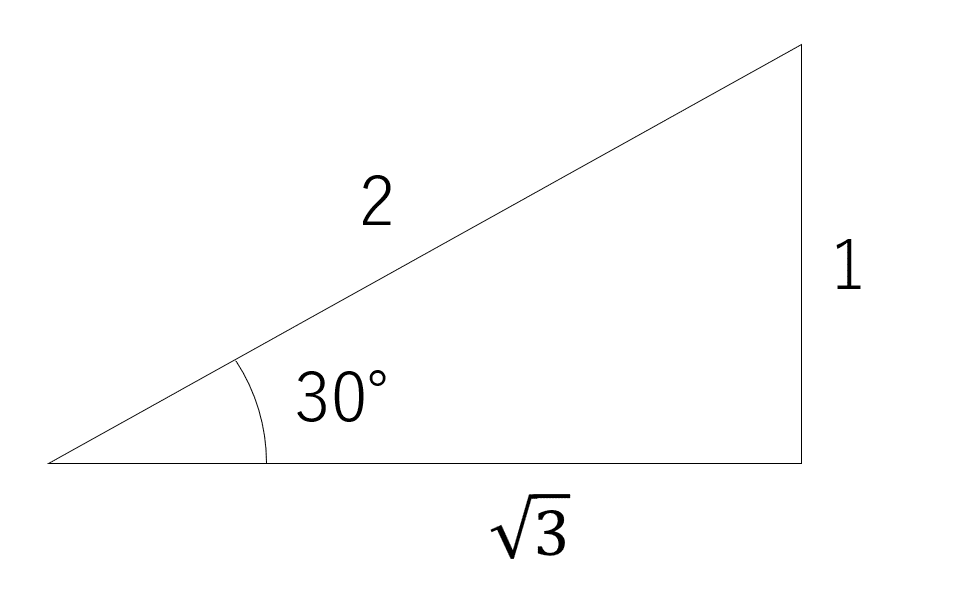
すると、三角関数の定義より、
$${sin30° = \frac{1}{2}}$$
$${cos30° = \frac{\sqrt{3}}{2}}$$
$${tanθ = \frac{1}{\sqrt{3}}}$$
てな感じになる。
これは$${0\lt\theta\lt90}$$の時に三角形で考えられるけど360度に拡張するために半径がrの円を使うね。
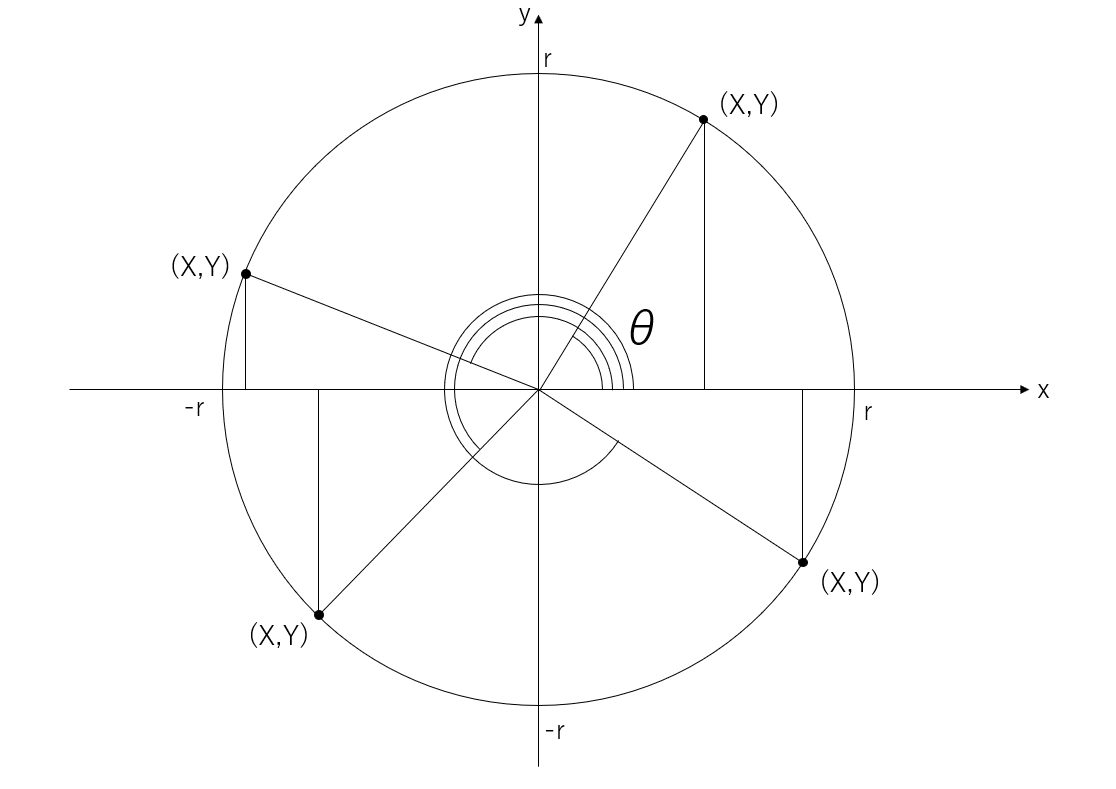
θは中心角で、円の中心から点までの距離はrで、X、Yは整数ね?そして、三角関数は次のように定義される!
$${sinθ = \frac{X}{r}}$$
$${cosθ = \frac{Y}{r}}$$
$${tanθ = \frac{Y}{X}}$$
また、上の図はθが正の数の時の図だけど、負の数の時は次のようになる!
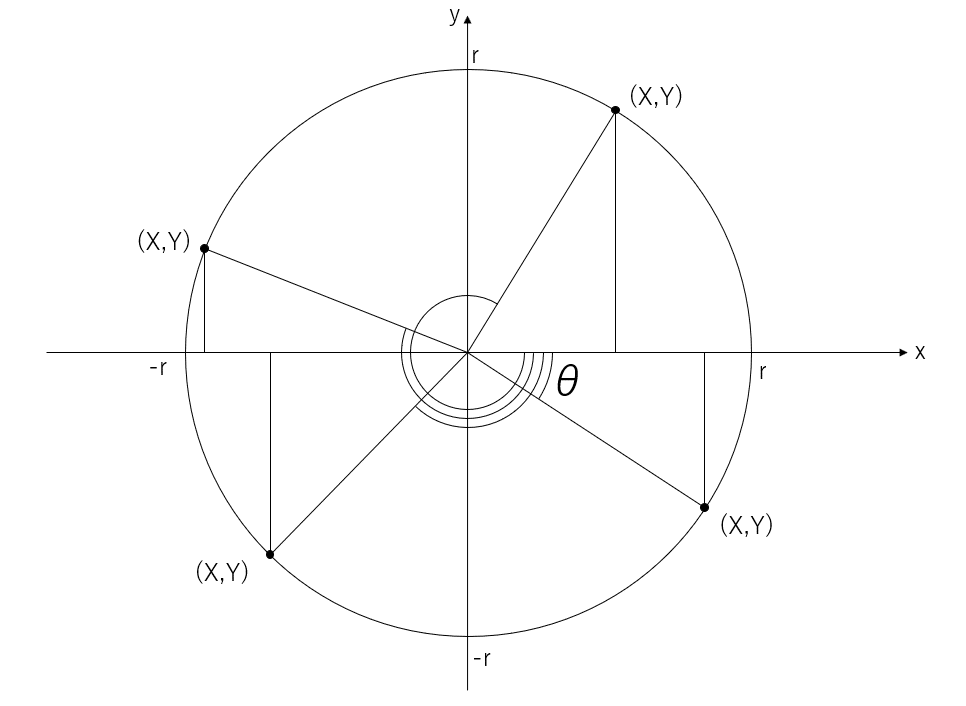
また、今までのθは30°とか60°とかって表してたよ?これを60分法っていうんだけど、実は弧度法っていう表記もあるんだ。
弧度法ってのは、さっき使ってた円の弧の長さをもとにして角度を表す方法だよ。また、弧度法の単位はラジアンっていうんだ。
例えば、60分法で30°を弧度法で表すと、
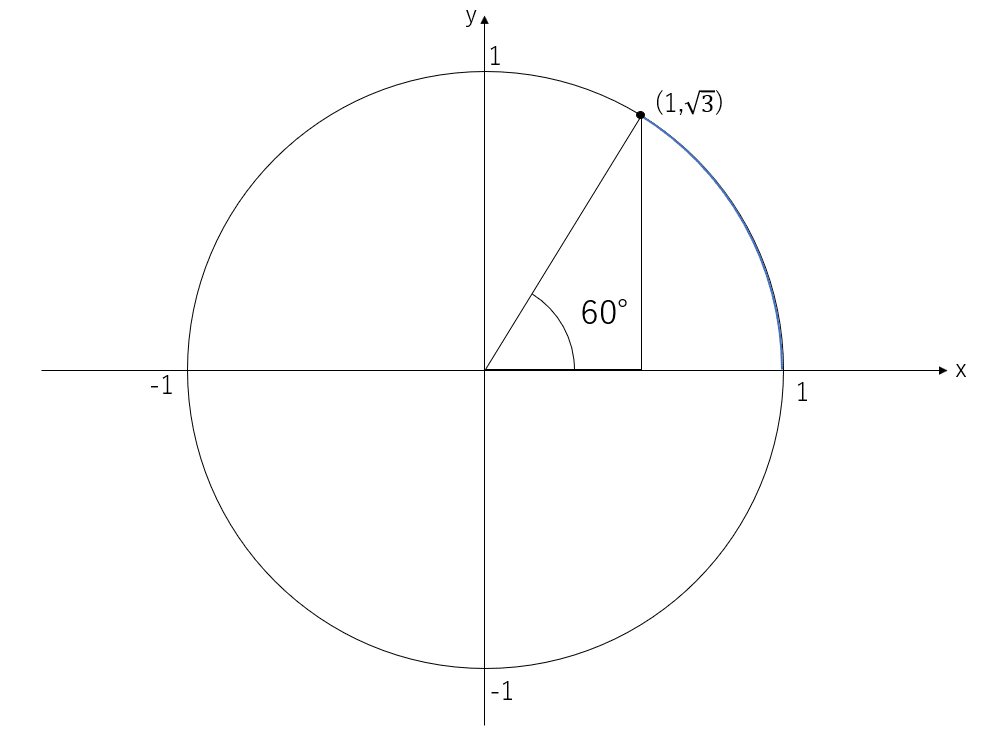
円周は半径が1だから2πで、60°って360°の$${\frac{1}{6}}$$だから、割合で考えると、青色の弧の長さは$${\frac{π}{3}}$$ラジアンってなる!
ここで一つ注意点があるんだけど、三角関数を使うときにθに°がついてたら60分法、何もついてなかったら弧度法で表記してることを表すからね。
ここで三角関数の公式を2つ紹介するよ。
$${sin^2θ + cos^2θ = 1}$$
$${tanθ = \frac{sinθ}{cosθ}}$$
今回は数学がメインじゃないから証明は省くけど難しくないから考えてみてね!
そういえばさっき半径がrの円を使って考えたけど半径が1の円は単位円っていうんだ。さっき紹介した定義に1を代入してみればわかるけど$${sinθ}$$は単位円上の点のy座標、$${cosθ}$$は単位円上の点のx座標を表してるよ!
ウィンドウアプリケーションの基礎知識
マロ:…というわけさ!
ミケ:おお、三角関数の復習にもなったよ!ありがと!
マロ:お安い御用だよ。
ミケ:さて、じゃあ今度は僕の番だね。
マロ:お!わくわく!
ミケ:さて、じゃあ説明していこうか~。
ユーザーインターフェイスとは
インターフェイス(interface)は英語で「接点」って意味があるよね?
そのため、ユーザーインターフェイスは人とコンピュータの接点って意味になるんだ。
例えばマウスやキーボード、スピーカーとかが想像つくと思うけど、もっとも代表的なのは「画面」だよね?
だって画面はコンピュータが情報を出力するのに一番必要なものだからね。
その画面で人とコンピュータはやり取りしていくわけだけど、そのやり取りにも二種類の方法があるんだ。
それは、主に文字を用いるCUIとグラフィックを用いるGUIの二つだよ。
CUIは僕たちになじみの深い$${System.out.println()}$$とかを用いればいいんだけど、GUIはそう単純にはいかないんだ。
ウィンドウの使い方
さきほど紹介したGUIにはいくつかの実現方法があるんだけど、今回はウィンドウUIを紹介するよ。
ウィンドウUIはOSのデスクトップに表示されたりするやつで、例えばウェブブラウザのchromeとかfirefoxとかだね。ほかにもVSCodeやEclipseなんかもウィンドウUIだよ。
そんなウィンドウUI なんだけど、もちろんその中核をなすのがウィンドウだよ。皆さんご存じの通り、長方形型で上のほうにタイトルバーがあるやつだね。ほとんどのアプリケーションは長方形のサイズも変えれたりできるね。
このウィンドウ、使い方は主に二つに分けれるんだ。
ウェジット
ウィンドウにテキストボックスやボタン、チェックボックスとかを設置して、そのボタンが押されたり、チェックが付けられたりしたら処理を実行する使いかた。これらの部品をウェジットっていうよ。
キャンバス
ウィンドウ全体を一つのグラフィック領域(絵を描くところ)として扱い、自由に文字や画像を描く使い方だよ。この領域をキャンバスというよ。
両者はそれぞれ使う場面が異なっていて、前者は業務アプリ(Word,Eclipse等)、後者はゲームの開発などにそれぞれ用いられるよ。
今回はアニメーションを作るから後者の使い方をするよ。
Swing API
今回は、さっきのキャンバスを実現する方法としてSwing APIを使うよ。
本来だったらJavaFXっていうAPIを使いたかったんだけど、残念ながらJava11でJDKと分離しちゃって独立したライブラリになっちゃったからね。
その点SwingはJDKに同梱されているから初心者にも扱いやすいし、何より僕が楽できるから今回はそっちを使っていくよ。
さて、Swingには主に三種類のウィンドウがあるよ。
枠やツールバーがないウィンドウ:javax.swing.JWindowクラス
枠やツールバーがあるフレーム :javax.swing.JFrameクラス
対話入力用の小さなダイアログ :javax.swing.JDialogクラス
今回はこの中のフレームを使っていくよ。
試しにウィンドウを表示させてみる
よし、じゃあ試しにウィンドウを表示させてみよう。
さっき説明したjavax.swing.JFrameクラスをインスタンス化して、setVisible()をよびだすことで画面にウィンドウを表示できるよ。
import javax.swing.*;
public class Main{
public static void main(String args[]){
JFrame window = new JFrame();
window.setTitle("僕はウィンドウだよ");
window.setDefaultCloseOperatioin(JFrame.EXIT_ON_CLOSE);
window.setBounds(500,500,400,300);
window.setVisible(true);
}
}意外と簡単でしょ?でも、実は複雑な処理が裏で行われているんだよ。
ウィンドウUIとスレッド
作ったウィンドウをドラッグして移動させたり、サイズを変えたりしてみてみて。当たり前だけど、ウィンドウは移動するしサイズも変わるよね。
では、上のコードのmainメゾットの末尾に以下の部分を追加してもう一度実行してみてほしい。
System.out.println("mainメゾットの終了");mainメゾットの末尾に記述してあるから、この処理が行われたらプログラムは終了しているはずだよね?
でも実際実行してみると、「mainメゾットの終了」と表示はされるけど、ウィンドウは消えたりしないよね。これはなんでなんだろう。
実はこれにはスレッドという仕組みが絡んでいるんだ。
スレッドっていうのは簡単に言うと、一つの処理の流れのことだよ。
今まではひとつの処理の流れ(メインスレッド)で作っていたけど、このスレッドを用いることで並列処理(複数の命令を同時に処理すること)が可能になるんだ。
話を戻すけど、Swingなどのウィンドウライブラリではウィンドウやウェジットを初めて生成する際に、メインスレッドとは独立した画面の描画や操作の管理と制御を行う専用のスレッド(UIスレッド)というものを実は起動しているんだ。
このスレッドによって、GUIの表示制御とか入力の待ち受けに使うような仕組みになっているっていうわけさ。
本当はもっとスレッドについて理解しておくべきなんだけど、今回は割愛させてもらうね。もっと詳しく知りたい方はここのサイトを参考にするといいかもしれない。
キャンバスを配置する
さて、小難しい話はこれくらいにして実際に描画するためのキャンバスを配置していこう。
今回は、javax.swing.JPanelクラスを使うよ。
このJPanelはウェジットとしてJFrameに配置することができるんだけど、更に自分自身のほかの部品を格納できるコンテナ(ウェジットを格納できる)としての機能も持っているんだ(多分今回は使わないから気にしなくていいと思うけどね)。
ということでJPanelの使い方だけど、今回は普通にJPanelをインスタンス化しないで、それを継承した匿名クラスのインスタンスをJPanel型の変数に代入して使うようにするよ(理由は後程説明するね)。
とりあえず、以下のように書いてみよう。
JFrame window = new JFrame();
JPanel canvas = new JPanel(){
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
//ここに描画処理
}
};これはJPanelクラスを継承したクラスのインスタンスをcanvasに代入しているって意味だね。
あと言い忘れていたけど、このままだとエラーが出るから
import java.awt.*;の一文を追加しておいてね。
なぜこのようにしているかというと、わざわざJPanelを継承して新たなクラスを作り、paintComponent()をオーバーライドするのがめんどくさいからだね。
このpaintComponent()内には描画の処理を書くよ。まぁ詳しくは後で説明するね。とりあえずは空欄でいいかな。
ではこれをウィンドウにはめ込んでみよう。JFrameインスタンスのadd()を使うよ。
window.add(canvas);add()の引数には、追加したいウェジットを指定するんだ。
今回の場合は、キャンバス(JPanel)だね。
さて、これで実行するとウィンドウは変わっている…というわけでもなく、なんも変化がないように見えるかもしれないね。
でも安心して。これはキャンバスになにも描画されていないからなんだ。
なんも書いていないキャンバスは真っ白だよね?それと同じさ。
ウィンドウを作るときに設定すること
さて、じゃあ次にJFrameインスタンスで画面を表示する前に設定できることを紹介するよ。
ウィンドウの初期位置を設定する
ウィンドウの初期位置、つまり画面が初めて表示された時の位置を設定することができるよ。その場合は、JFrameインスタンスのsetLocation()を呼び出すよ。
window.setLocation(500,500);//画面の左上から500px 500pxの位置に設定ウィンドウの初期サイズを設定する
ウィンドウの初期サイズを設定することができるよ。その場合はJFrameインスタンスのsetSize()を呼び出すよ。
window.setSize(500,500);//500x500のサイズに設定する。ウィンドウのタイトルを設定する
ウィンドウバーに表示される文字列を設定することができるよ。その場合はJFrameインスタンスのsetTitle()を呼び出すよ。
window.setTitle("タイトルだよ");×ボタンを押したときの処理を設定する
ウィンドウバー右上のよく見る赤い"アレ"を押したときの処理を設定できるよ。その場合はJFrameインスタンスのwindow.setDefaultCloseOperatioin()を呼び出すよ。
//ボタンを押したらウィンドウを閉じる
window.setDefaultCloseOperatioin(JFrame.EXIT_ON_CLOSE);この引数にはJFrameの静的フィールドEXIT_ON_CLOSEが指定されているけど、ほかにもHIDE_ON_CLOSEやDO_NOTHING_ON_CLOSEが静的フィールドとして用意されているけど、いまはEXIT_ON_CLOSEだけ覚えとけばいいかな…。ちなみに、初期状態ではHIDE_ON_CLOSEになっているよ。
ウィンドウの初期位置と初期サイズを同時に設定する
ウィンドウの初期位置と初期サイズを同時に設定する際は、JFrameインスタンスのsetBounds()を呼び出すよ。
window.setBounds(500,500,400,300);//500,500の位置に400x300のサイズウィンドウを表示する
ウィンドウを表示する際はJFrameインスタンスのsetVisible()を呼び出すよ。
window.setVisible(true);trueなら表示、それ以外なら非表示になるね。
なお、この命令はウィンドウの設定が終わった後に呼び出すよ。
実際に描画していく
さて、じゃあ実際にキャンバスに描画をしていこう。
さっきも言ったけど、キャンバスに描画するにはJPanelのpaintComponent()に処理を書いていくんだったね。
//再掲
JPanel canvas = new JPanel(){
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
//ここに描画処理
}
};具体的に言うなら、引数のGraphicsクラスの持つメゾットを呼び出して描画していくよ。
ここで、いったんGraphicsクラスに備わるメゾットを確認してみよう。
APIリファレンスを見てみると….。
沢山のメゾットがあるね!!! こんなに多かったら使いきれないよ~って思うかもしれないね。 大丈夫、ぶっちゃけこの中でも二つくらいしか今回は使わないから(笑)
じゃあその二つのメゾットだけ紹介しておくね。
今回使うのは…
setColor(Color c)
fillOval(int x, int y, int width, int height)
だよ!
前者は描画する際の色を決めて、後者は楕円もしくは円の塗りつぶしを描画するよ。
ちなみに、setColor()の引数のColorはjava.awt.ColorクラスのColorで、内部に色のデータを持つよ。まぁ普通はColorクラスの静的フィールドを使えばいいんだけどね。
ということで、試しに赤色の円を書いてみよう。
protected void paintComponent(Graphics g) {
super.paintComponent(g);
//ここに描画処理
g.setColor(Color.red);
g.fillOval(50,50,10,10);//x:50 y:50 半径5の円
}このように記述して、実行してみよう!
まぁこんな感じになればOKかな。
円を移動させてみる
円を描画できたところで、次はこの円を動かしてみよう。
やることとしては、次の三つだね。
円の座標を保持する変数(x,y)を作る
x,yの値を変更させる
x,yを使って円を描画する
では、これを実装するためにjavax.swing.Timerクラスを使っていこう。
このTimerクラスは、与えた処理を一定時間ごとに実行させることができるんだ。詳しくは、APIリファレンスを参考に。
実際に使ってみたコードがこれだよ。
import java.awt.*;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import javax.swing.*;
public class Main{
static int x,y;
public static void main(String[] args) {
x=0;y=0;
JFrame frame = new JFrame();
frame.setTitle("三角関数のテスト");
frame.setSize(500,500);
frame.setLocationRelativeTo(null);//画面の真ん中に配置する
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
JPanel canvas = new JPanel(){
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
g.setColor(Color.red);
g.fillOval(x-5, y-5, 10, 10);
}
};
frame.add(canvas);
frame.setVisible(true);
Timer timer = new Timer(10, new ActionListener(){
@Override
public void actionPerformed(ActionEvent e) {
x++;
y++;
canvas.repaint();
}
});
timer.start();
}
}canvas.repaint()っていうのはもう一度描画処理を行うっていう意味だよ。
x,yが変化した状態でもう一度描画する必要があるからね。
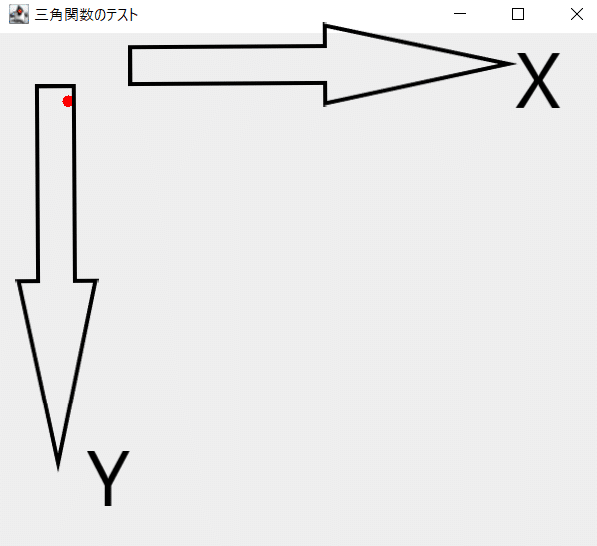
…とまぁこうすることで、円が左上から右下に移動するはずだよ。
もしかしたら気づいたかもしれないけど、ウィンドウ上のY座標は下方向が正になるよ。
数学でいうところの第二象限だね。
これがあとで重要になってくるから覚えておいてね。
実際に作っていこう!
ミケ:…ってことなんだけど、どうかな?わかった?
マロ:なんとなくわかった気がする!
まだここまでなら僕でも理解できるかなぁ?
でもこういうの見てると、わかりやすく伝えたりそれを理解して使いこなしたりしたりしてすごいな~って感じるよ!
ミケ:(∀`*ゞ)エヘヘ~ まぁ基礎知識はこれくらいで実際に作っていこうか!
マロ:おお! わくわく~!
円運動をさせてみる
さて、じゃあためしに簡単な円運動を書いてみようか。
マロの言った通り、角度$${\theta}$$の時の円上のX,Y座標は次のように表せるよ。
$${Y = r\sin \theta }$$ $${X = r\cos \theta }$$
この式に従って$${\theta}$$の値を動かすことで、円運動をする際のX,Yの値が求まるってわけさ。
では、この時の$${r}$$は何を表すと思う?
そう、原点(円の中心)からの距離を表すんだ。 まぁ当たり前だよね。
ということで、書いてみよう!
import java.awt.Graphics;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.Color;
import javax.swing.*;
public class TrigonometricTest{
static int x=0;
static int y=0;
static int deg=0;
static int distance=100;
public static void main(String[] args) {
JFrame frame = new JFrame();
frame.setTitle("三角関数のテスト");
frame.setSize(500,500);
frame.setLocationRelativeTo(null);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
JPanel canvas = new JPanel(){
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
draw(g);
}
};
frame.add(canvas);
frame.setVisible(true);
Timer timer = new Timer(10, new ActionListener(){
@Override
public void actionPerformed(ActionEvent e) {
// ここで動きの処理
x=(int)(Math.cos(Math.toRadians(deg))*distance)+250;
y=(int)(Math.sin(Math.toRadians(deg))*distance)+250;
deg++;
System.out.println(x+":"+y);
x++;
y++;
canvas.repaint();
}
});
timer.start();
}
public static void draw(Graphics g){
// ここに描画内容を書いていく
g.setColor(Color.red);
g.fillOval(x-5, y-5, 10, 10);
}
}
ここでは、描画処理はdraw()にまとめているよ。
$${\sin}$$と$${\cos}$$の値は、Mathクラスの静的メゾットであるMath.sin()とMath.cos()でそれぞれ求められるね。
角度はdegree(°)で扱うことにしているよ。 ラジアンだと小数値になるのに対して、度で表すと整数値として扱えるからね。
ただ、Math.sin(),Math.cos()の引数にはラジアン値を指定しないといけないから、度で扱っている角度をラジアンに変換する必要があるね。
そのために、Mathクラスの静的メゾットのMath.toRadians()を使っているんだ。 引数には度を与えるよ。
なお、度を格納する変数をそのままMath.toRadians()の引数に指定している理由は角度が360度を超えると一回転していることになるから、角度が360以上でも機能するからだよ(下図参照)。
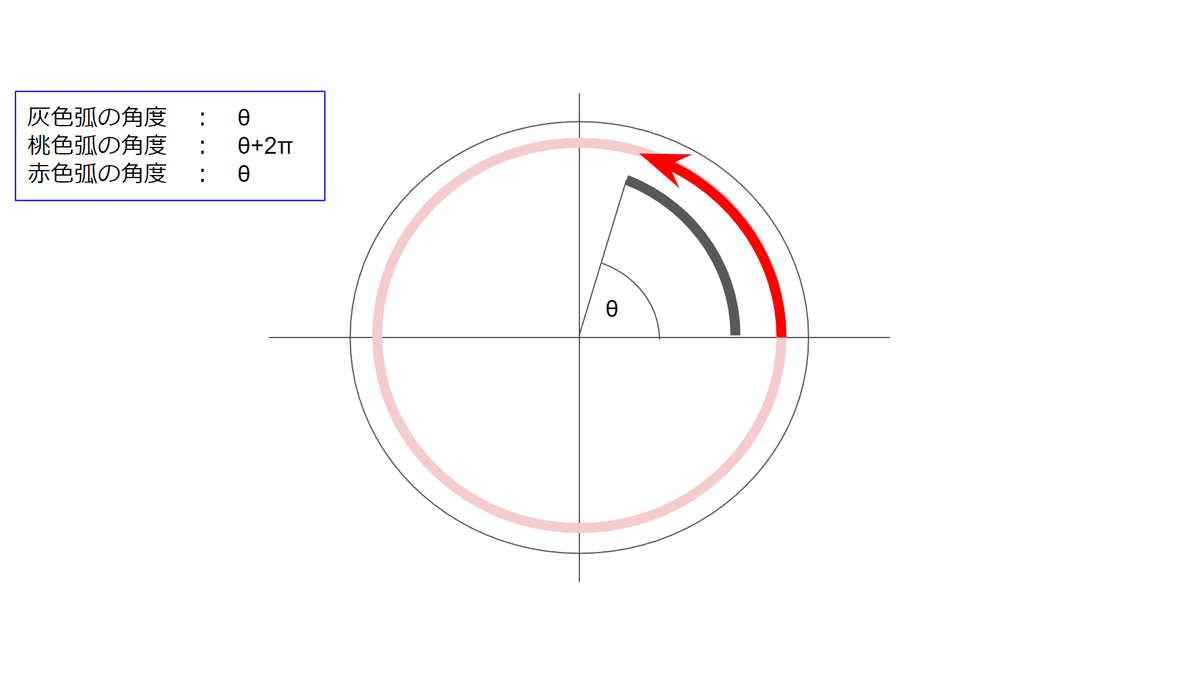
すなわち、三角関数で角度$${\theta}$$において、$${n \in \Z}$$であるとき次のことが成り立つんだ
$${\sin (\theta+2\pi n)=\sin \theta }$$
$${\cos (\theta+2\pi n)=\cos \theta }$$
$${\tan (\theta+2\pi n)=\tan \theta }$$
ただ、これだとdegがオーバーフローするかもしれないね。
でも大丈夫、オーバーフローするには円が約5840000回以上回転する必要があるからね。そんなに回転させないでしょ? (しないよね?)
ホーミング弾を打ってみる
さて、じゃあ次にホーミング弾を作ってみよう!!
とりあえず、縦に動く弾に対してホーミング弾を打ってみよう。

問題は、どうやって追尾するかだよね?
もっと具体的に言えば、弾と目標との角度が分かれば、sinとcosで進むことができるよね。
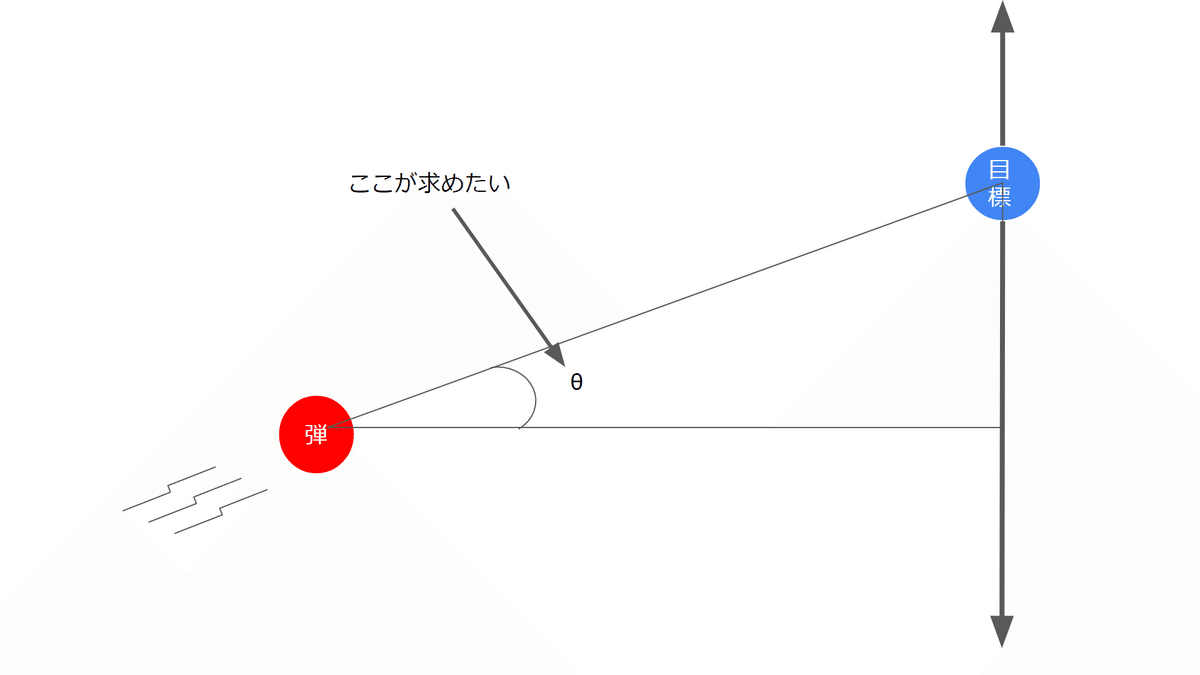
では、ここで求められることを整理しよう。
求めることができるのが次の二つだね。
弾と目標とのX座標の距離
弾と目標とのY座標の距離
この二つを使って、何とか$${\theta}$$を求められないかな…。
ところで話は変わるけど、逆関数って知ってるかな。
逆関数っていうのは大まかにいえば次のような関係を持つ関数のことだよ。
$${y=f(x)}$$の時$${x=g(y)}$$
例えば、$${\sin x}$$の逆関数である$${\arcsin x}$$はxに三角関数の値を入れることで、その時の角度が帰ってくるってわけさ。
(余談だけど、$${\sin( \arcsin( \frac{1}{2}))=\frac{1}{2}}$$ってなんか面白くない?)
じゃあ$${\tan x}$$の逆関数を考えてみよう。
$${\tan x}$$ の逆関数、$${\arctan x}$$では引数に$${\frac{隣辺}{対辺}}$$を指定して、その時の三角形の角度を返すよね。
もしかしたら勘のいいひとはもう気が付いたかもしれないね。
そう、この$${\arctan}$$を使えば二つの辺の比だけで角度が求められるんだ!
すなわち、弾と目標とのX,Y座標の距離さえ求めれば、弾と目標との角度$${\theta}$$が求めれるんだね。
(ぶっちゃけ二辺から斜辺(弾と目標との直線距離)を求めて、sinかcosの逆関数で角度を求めることもできるんだけど、それでもtanの逆関数をつかう理由は単純に計算する量が少なくなるからだよ。 斜辺を計算するとなったら平方根求めないといけなくなるからね。)
さて、Javaでtanの逆関数を求めるメゾットを紹介するよ。
Math.atan2(縦座標,横座標)ちなみに、Math.atan()というものもあるけどそれぞれちょっと違いがあるよ。簡単に言うなら、Math.atan()は先ほど言ったtanの逆関数で変域は
$${-\frac{\pi}{2}\lt atan\lt\frac{\pi}{2}}$$だよ。
それに対してMath.atan2()はxy直行座標における偏角を返して、変域は
$${-\pi\lt atan2\lt\pi}$$だよ。
ということで書いてみたのがこちら
import java.awt.Graphics;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.Color;
import javax.swing.*;
public class TrigonometricTest{
static int x=0;
static int y=0;
static int speed = 2;
static int targetX = 400;
static int targetY = 100;
static int targetSpeed = 2;
public static void main(String[] args) {
JFrame frame = new JFrame();
frame.setTitle("三角関数のテスト");
frame.setSize(500,500);
frame.setLocationRelativeTo(null);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
JPanel canvas = new JPanel(){
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
draw(g);
}
};
frame.add(canvas);
frame.setVisible(true);
Timer timer = new Timer(10, new ActionListener(){
@Override
public void actionPerformed(ActionEvent e) {
// ここで動きの処理
targetY += targetSpeed;
double ang = Math.atan2(targetY-y, targetX-x);
y+=Math.sin(ang)*speed;
x+=Math.cos(ang)*speed;
targetSpeed*=(targetY+10>500 || targetY-10<0 ? -1 : 1);
canvas.repaint();
}
});
timer.start();
}
public static void draw(Graphics g){
// ここに描画内容を書いていく
g.setColor(Color.red);
g.fillOval(x-5, y-5, 10, 10);
g.setColor(Color.blue);
g.fillOval(targetX-10, targetY-10, 20, 20);
}
}
さっきの円運動とちょっと違うところもあるけど、ほとんど同じだね。
まぁ正直これだとホーミングが強すぎだから、ちょっと角度を取得する間隔を変えたりするといいんじゃないかな?
そこあたりは自分で調整してくださいね~。
シューティングゲームで使えそうな弾幕を打ってみる
よし、じゃあ最後にシューティングゲームで使えそうな弾幕を張ってみようか。 とはいっても、簡単だから安心してね。
弾幕を張るということは、等間隔に弾を置いていけばいいわけだよ。
となると、まず自分の向いている向きを中心としてそこから$${\pm n \degree}$$ずらしていけばいいだけだね。
となると、こういう風になるかな。
import java.awt.Graphics;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.Color;
import javax.swing.*;
public class TrigonometricTest{
static int x=50;
static int y=250;
static Bullet bls[] = {new Bullet(x,y),new Bullet(x,y),new Bullet(x,y),new Bullet(x,y),new Bullet(x,y),};
public static void main(String[] args) {
JFrame frame = new JFrame();
frame.setTitle("三角関数のテスト");
frame.setSize(500,500);
frame.setLocationRelativeTo(null);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
JPanel canvas = new JPanel(){
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
draw(g);
}
};
frame.add(canvas);
frame.setVisible(true);
Timer timer = new Timer(10, new ActionListener(){
@Override
public void actionPerformed(ActionEvent e) {
// ここで動きの処理
for (int i = 0; i < bls.length; i++) {
bls[i].x+=(int)(Math.cos(Math.toRadians(30*(i-2)))*5);
bls[i].y+=(int)(Math.sin(Math.toRadians(30*(i-2)))*5);
}
canvas.repaint();
}
});
timer.start();
}
public static void draw(Graphics g){
// ここに描画内容を書いていく
g.setColor(Color.red);
g.fillOval(x-10, y-10, 20, 20);
g.setColor(Color.blue);
for (int i = 0; i < bls.length; i++) {
g.fillOval(bls[i].x-5, bls[i].y-5, 10, 10);
}
}
}
class Bullet{
int x;
int y;
Bullet(int x,int y){
this.x=x;
this.y=y;
}
}
これは中心から30度ずつ離して弾を打っているよ。
弾を格納している配列の要素を増やせば、もっとたくさん弾が出てくるようになるよ。
色々いじって試してみてね。
終わりに
どうやらすっかり暗くなって、雨もやんでいました。
ミケ:ふぅ~、やっと終わったぁ~。
マロ:結構ながかったよねぇ~。
ミケ:うん、思ったより時間がかかっちゃった。
マロ:でもすごく達成感があるような気もする!ウィンドウについてもイメージをつかめたはず?
ミケ:なんで最後疑問形なの?w でも、達成感あるならよかった!
マロ:お、いつの間にか雨がやんでるみたいだね。
ミケ:でも、もう真っ暗かぁ。 あそびにいけないじゃん…。
マロ:まぁいいじゃん、今日くらい。たまにはこうやって話すのもさ。
ミケ:確かに、たまにならいいかもね。でも、ちょっとは運動しないと…。
マロ:ん~、じゃあちょっとだけ散歩しよっか。飼い主さんも帰ってくるのにもうちょっと時間かかるし。
ミケ:やったぁ! いくぞ~!
マロ:そんなに走っちゃだめだよ~!
月の明かりが散歩する二匹を優しく照らしています。
二匹は飼い主さんが帰ってくるまでの間、ちょっとの散歩を楽しみました。
まぁ二匹とも遠くまで散歩しすぎて、飼い主さんに怒られてしまったのですが…。
by マロ&ミケ
ーーーーもし間違い等ございましたらご報告くださいーーーー
