【アルゴリズム】O記法ってなに?初心者必見、プログラムの計算時間を見積もる。
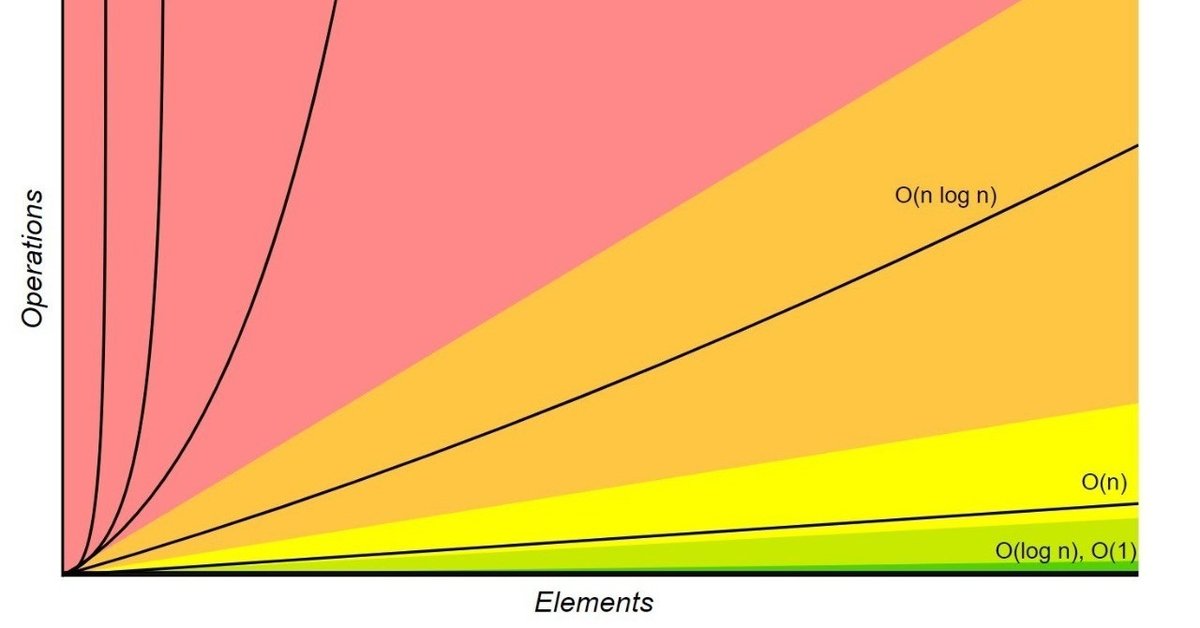
O記法(オーダー記法)とは計算にかかる時間とデータ量の関係について表した記法です。
O(n) とかO(log n)ってよく見かけると思います。あれのことです。
読み方はO(オー)です。0(ゼロ)ではないのでご注意を。()の中は処理するデータ量です。
記法って何?って思うかもしれませんが、シンプルに、世界共通の表現方法としていてくだい。「このアルゴリズムの計算時間はどれぐらい?」と聞かれた時、他人に説明できる世界共通の基準があると便利ですよね。
O記法は、サンプルプログラムを見た方が早いです。
O(1)
function log(arr) {
console.log(array[0]);
console.log(array[1]);
}
log([1, 2, 3, 4]);
log([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]);O(1)はデータ量がどんなに増えても、常に一回しか処理を行わないことです。例を見ると、配列の要素に直接アクセスしていますよね。データ量が1つだろうが100万だろうが、常にarrayの[0]と[1]番目だけアクセスしています。
一番高速です。
グラフにすると分かりやすいです。データ量が増えても計算量は一定です。

O(n)
function logAll(array) {
for (let i = 0; i < array.length; i++) {
console.log(array[i]);
}
}
logAll([1, 2, 3, 4, 5]);
logAll([1, 2, 3, 4, 5, 6]);
logAll([1, 2, 3, 4, 5, 6, 7]);次はO(n)です。データ量(n)が増えただけ、計算量も増えます。これは直感的で分かりやすいと思います。
計算量はデータ量に比例します。
グラフを見ると一目瞭然ですね。

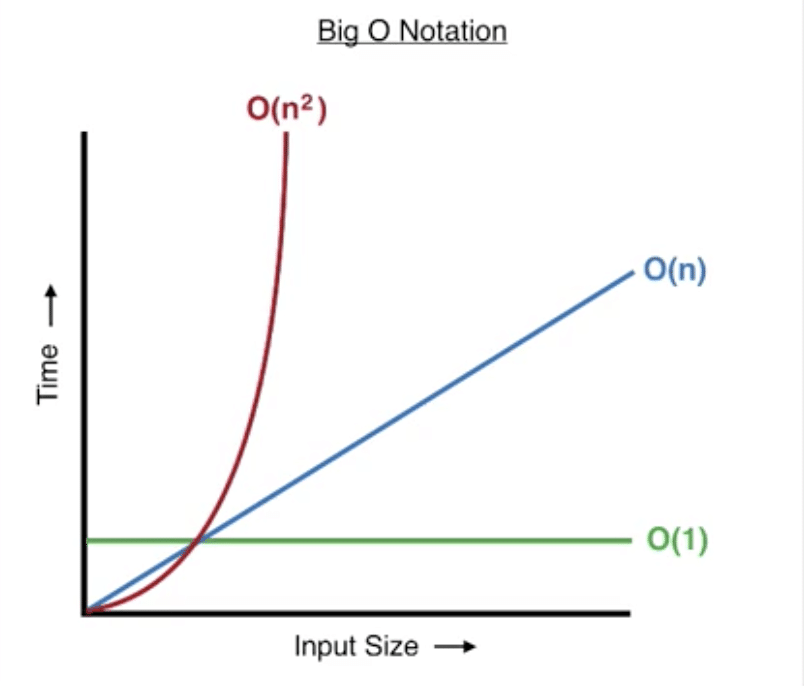
O(n^2)
function addAndLog(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
console.log(array[i] + array[j]);
}
}
}
addAndLog(["A", "B", "C"]); // 9つの組み合わせ
addAndLog(["A", "B", "C", "D"]); // 16の組み合わせ
addAndLog(["A", "B", "C", "D", "E"]); // 25の組み合わせ次のO(n^2)ですが、「^」ってのは累乗するって意味です。2乗なのでn * nですね。
サンプルプログラムを見てみましょう。配列の文字で、何通りの組み合わせができるか出力するプログラムです。今度はループが2重になってますね。
計算量は 外側ループのarray長さ * 内側ループのarray長さになります。
3 * 3 = 9回の処理はたいしたことないですが、5 * 5 で25に一気に処理回数が増えます。
100 * 100 だったらどうでしょう?グラフを見てもらえばわかると思いますが、これはあまりよろしくないですね。。
計算量は指数関数的に増えていきます。できるだけ避けたいアルゴリズムです。
O(log n)
function binarySearch(array, key) {
var low = 0;
var high = array.length - 1;
var mid;
var element;
while (low <= high) {
mid = Math.floor((low + high) / 2, 10);
element = array[mid];
if (element < key) {
low = mid + 1;
} else if (element > key) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}
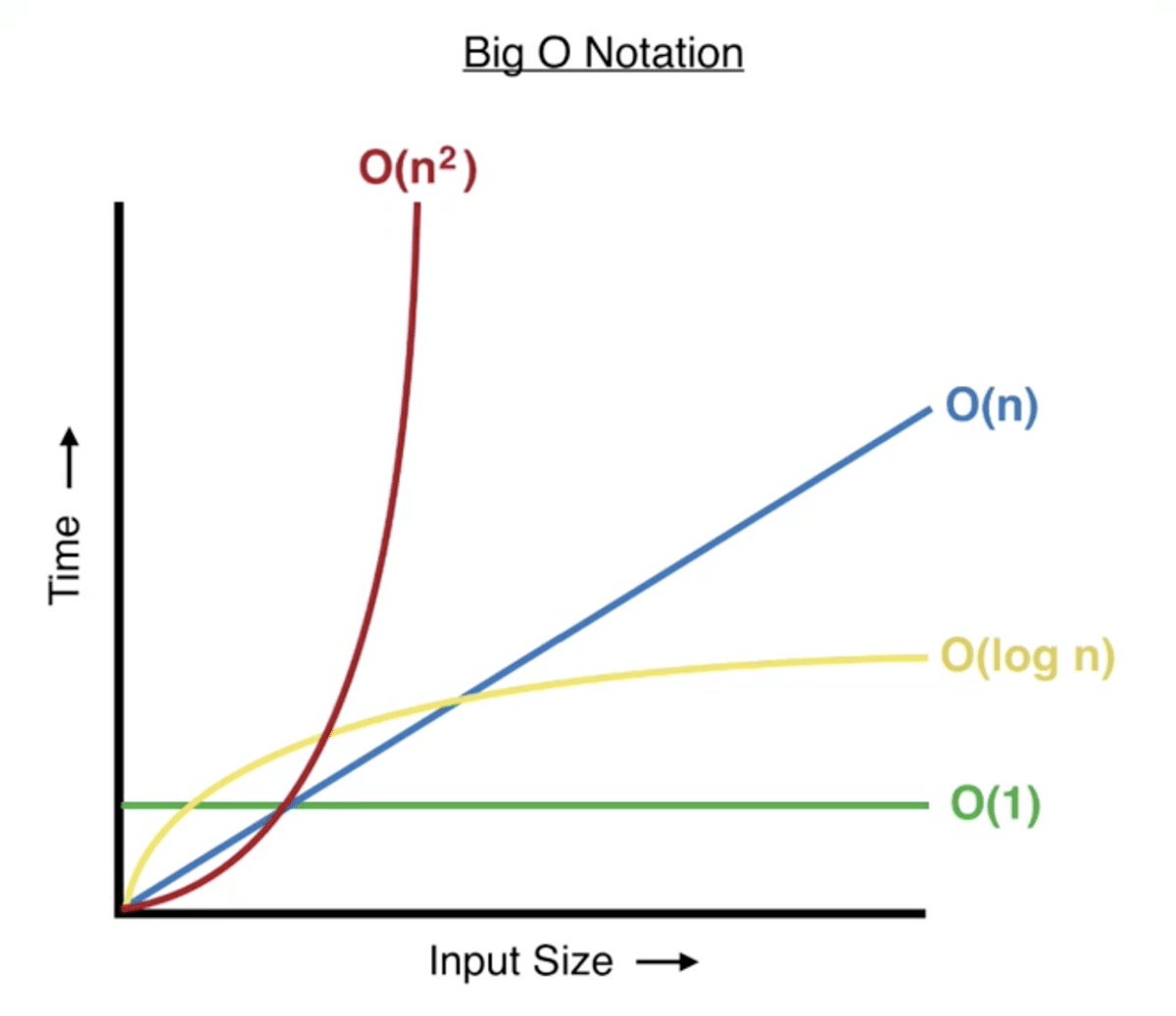
console.log(binarySearch([1, 2, 3, 4, 5, 6], 3));最後はO(log n)です。オーのログ nって呼んでください。ズバリこれは、データ量に対して、計算量が常に半分になっていくことです。
サンプルは二分探索ですが、辞書から単語を探す例の方が、分かりやすいかもしれません。
例えば「HOUSE」って言葉を辞書から探すとしましょう。26文字あっても常に探す範囲は半分になってますね。4回の処理で完了しています。(現実にはこんなことしないですが。。)
ABCDEFGHIJKLMNOPQRSTUVWXYZ
ABCDEFGHIJKL
GHIJKL
GHI
H
O(log n)はこの辞書をイメージしてもらえれば分かりやすいと思います。二分探索だとデータ量が4000あったとすると、12回の処理で完了します。
メッチャ早いですね。
O(n^2)の対極だと思ってください。
以上、代表的なものを紹介してきました。ほんとは、もっとあるんですけど、とりあえずこれだけ覚えてください。これを意識できるかで、プログラムを見る目が全然違ってきます。最悪O(n)を超えないように、プログラムを書いていけば、まずは大丈夫だと思います。
良いアルゴリズムとは、問題の規模が大きくなっても対応できるということです。
私も初心者のころは、いつもO(n^2)のプログラムを書いて、いざ環境がプロダクションになると、クラッシュさせてました。。
O記法(オーダー記法)の説明が一番わかりやすい本です!
↑の本を読んでみたら、以下2冊もチャレンジしてみてください。どんなプログラムを組むにしろ一回は読んで欲しい名著です。
