
動かして学ぶバイオメカニクス#13 〜全身の力学解析(補足)〜
前章でコードを全て示した.ここでは,第11章と第12章を振り返りながら,力学計算とコードについて補足する.
オイラーの運動方程式の解法
再帰呼び出しによるオイラーの運動方程式の解法は第11章で述べたが,ここでは第12章で示したコードとの関係を補足する.
座標変換
オイラーの運動方程式では,部位$${i}$$の慣性力は各部位(link)に固定されたローカル座標系で一旦計算するほうが有利であり,一方,モーションキャプチャを使用して力のモーメントやトルクを計算する場合は絶対座標系(モーションキャプチャ座標系)で計算するほうが容易であり,異なる部位間の計算を行う場合には最終的には絶対座標系で統一して計算する必要がある.
慣性力であれば,
$$
{}^0\bm{R}_i\left(\bm{I}_i ^i \dot{\bm{\omega}}_i^i+ \bm{\omega}_i^i \times (\bm{I}_i^i \bm{\omega}_i^i) \right)
$$
のように,一括して$${{}^0\bm{R}_i}$$でローカル座標系$${i}$$から絶対座標系$${0}$$に座標変換を行えばよい.
また,一旦,絶対座標系でトルクを計算しても,その物理的意味を理解するには,再びローカル座標系の変換することも必要であろう.そこで,座標変換は頻繁に使用することになる.
座標変換行列$${{}^0\bm{R}_i}$$は$${3\times3}$$の行列であるが,3つの直交する単位ベクトル(正規直交基底)から構成されるので,クラスBodyLinkのインスタンス変数rotに格納しておく際には,ローカル座標系から絶対座標系へ,または絶対座標系からローカル座標系への変換に対応しやすいように,3つの単位ベクトルを並べた配列に保持している.具体的には
b_link[1].rot
>>>
array([[[ 0.99830339, -0.05134678, 0.02745627],
[ 0.99827793, -0.05179752, 0.02753516],
[ 0.99825407, -0.05221242, 0.02761661],
...,
[ 0.96157907, 0.26909069, 0.05436812],
[ 0.96160586, 0.26894361, 0.05462145],
[ 0.96162459, 0.26882198, 0.05488976]],
[[ 0.05316219, 0.99612346, -0.07008446],
[ 0.05360784, 0.99612819, -0.06967662],
[ 0.05401803, 0.99613403, -0.06927522],
...,
[-0.27452023, 0.94400807, 0.18299565],
[-0.27442403, 0.94405126, 0.18291712],
[-0.27435565, 0.94408553, 0.18284282]],
[[-0.02375123, 0.07142519, 0.99716314],
[-0.02381947, 0.07103273, 0.99718954],
[-0.02389281, 0.07064606, 0.99721526],
...,
[-0.00208152, -0.19088993, 0.98160924],
[-0.00237106, -0.19088362, 0.98160981],
[-0.00266846, -0.19088546, 0.98160869]]])の形式で格納する.これを,利用して行列を並べる形式にする関数が
rot_vec2mat_local(rot_vec) # 絶対座標系からローカル座標系へ
rot_vec2mat_global(rot_vec) # ローカル座標系から絶対座標系へで,
rot_vec2mat_global(b_link[1].rot)
>>>
array([[[ 0.99830339, 0.05316219, -0.02375123],
[-0.05134678, 0.99612346, 0.07142519],
[ 0.02745627, -0.07008446, 0.99716314]],
[[ 0.99827793, 0.05360784, -0.02381947],
[-0.05179752, 0.99612819, 0.07103273],
[ 0.02753516, -0.06967662, 0.99718954]],
[[ 0.99825407, 0.05401803, -0.02389281],
[-0.05221242, 0.99613403, 0.07064606],
[ 0.02761661, -0.06927522, 0.99721526]],
...,
[[ 0.96157907, -0.27452023, -0.00208152],
[ 0.26909069, 0.94400807, -0.19088993],
[ 0.05436812, 0.18299565, 0.98160924]],
[[ 0.96160586, -0.27442403, -0.00237106],
[ 0.26894361, 0.94405126, -0.19088362],
[ 0.05462145, 0.18291712, 0.98160981]],
[[ 0.96162459, -0.27435565, -0.00266846],
[ 0.26882198, 0.94408553, -0.19088546],
[ 0.05488976, 0.18284282, 0.98160869]]])
のように,これらの関数によって,座標変換行列を並べる形式に変換する.
慣性力
絶対座標系に変換した慣性力$${{}^0 \bm{R}_i\left(\bm{I}_i ^i \dot{\bm{\omega}}_i^i+ \bm{\omega}_i^i \times (\bm{I}_i^i \bm{\omega}_i^i) \right)}$$は,このコードの中では関数Inertial_Force_global()
# 慣性力(絶対座標系)
def Inertial_Force_global(self):
return frame_trans_global(self.rot,
self.inertia_moment * self.dot_w + \
np.cross(self.w, self.inertia_moment * self.w))で計算される.対象とする部位をselfと考えれば,その部位の慣性テンソルはself.inertia_momentに代入され,self.dot_wがその部位の角加速度,self.wが角速度である.対応関係をよくご覧になっていただければと思う.
なお,self.inertia_momentはベクトルとして格納している.運動方程式ではたとえば$${\bm{I} \dot{\bm{\omega}}}$$のように,テンソルとベクトルの積で記述されるが,$${3 \times 3}$$の行列で表現されるテンソルはいま対角行列なので,対角行列とベクトルの積は,ベクトルとベクトルのアダマール積で計算するほうが,無駄な計算が少ないため,単にself.inertia_moment * self.dot_wのようにベクトルとベクトルの単純な積(アダマール積)で計算を行っている.
最後に,frame_trans_global(self.rot, vec)で絶対座標系に変換する.vecには慣性力のベクトル(self.inertia_moment * self.dot_w + np.cross(self.w, self.inertia_moment * self.w)を与えればよい.
この計算結果は,今回の力学計算では保持しておく必要がないが,クラスBodyLinkのインスタンス変数としてself.inertial_globalを準備し,再帰呼び出しによって関節に作用するトルクを計算するメソッド関数ID_Euler()では
inertial_global = self.Inertial_Force_global()
self.inertial_global = inertial_globalのように,インスタンス変数self.inertial_globalに代入して保持している.これは,後々,この慣性力がどの程度貢献しているのかを,検証する際に有用となる.
力のモーメント
各部位$${i}$$には「重心$${\bm{x}_{gi}}$$まわり」の力のモーメントとして,
$$
{}_{gi}^{i}\bm{p} \times \bm{f}_{i} + {}_{gi}^{i+1}\bm{p} \times (-\bm{f}_{i+1})
$$
が作用する.ただし,末端部分では力が作用しないので,力のモーメントを計算する関数Joint_Moment_global()のコード
# 関節に作用する力のモーメント
#(★ 221221訂正)
def Joint_Moment_global(self):
# ★ 221221訂正)
# 末端のdistal endのext_momentに外力(フォースプレートのモーメント等)が入力されている場合は,外力も取り込む
#(ID_Joint_Moment_global()で外力を計算していたが,Joint_Moment_global()で外力を取り込むように変更
if np.any(self.ext_moment) != None:
return np.cross(self.p - self.cg, self.force) + self.ext_moment
# 近位側に作用する力のモーメント
elif np.any(self.child_val.force) == None:
return np.cross(self.p - self.cg, self.force)
# 近位側と遠位側の両方の関節に作用する力のモーメント
else:
return np.cross(self.p - self.cg, self.force) + \
np.cross(self.child_val.p - self.cg, -self.child_val.force)では,np.any(self.ext_moment) != Noneのif文で,末端のdistal endのext_momentに外力(フォースプレートのモーメント等)が入力されている場合は,外力を取り込み,np.any(self.child_val.force) == None のif文で,遠位端に力が作用するかどうかをを判断し,作用しない場合は原点の力のモーメントだけを計算する.
この計算結果は,同様に今回の力学計算では保持しておく必要がないが,クラスBodyLinkのインスタンス変数としてself.inertial_globalを準備し,再帰呼び出しによって関節に作用するトルクを計算するメソッド関数ID_Euler()の
j_moment_global = self.Joint_Moment_global()
self.j_moment_global = j_moment_globalで,インスタンス変数self.j_moment_globalに代入して保持している.これは,後々,この力のモーメントがが,身体運動に置おいてどのように貢献しているのかを,検証する際に有用となる.
関節に作用するトルク
第11章で述べたように,関節に作用するトルクは
$$
\bm{\tau}_i^0 = {}^0 \bm{R}_i\left(\bm{I}_i ^i \dot{\bm{\omega}}_i^i+ \bm{\omega}_i^i \times (\bm{I}_i^i \bm{\omega}_i^i) \right) + \left(-{}_{gi}^{i}\bm{p}^0 \times \bm{f}_{i}^0 + {}_{gi}^{i+1}\bm{p}^0 \times \bm{f}_{i+1}^0 \right) + \bm{\tau}_{i+1}^0
$$
を再帰呼び出しで計算するが,関数Torque()は,このうち右辺の最後の項$${ \bm{\tau}_{i+1}^0 }$$を除いて,
# 関節に作用するトルク
def Torque(self):
# linkの遠位端の関節に力が作用する場合
if np.any(self.child_val.force) != None:
return frame_trans_global(self.rot,
self.inertia_moment * self.dot_w +\
np.cross(self.w, self.inertia_moment * self.w)) -\
np.cross(self.p - self.cg, self.force) + \
np.cross(self.child_val.p - self.cg, self.child_val.force)
# linkの遠位端の関節に力が作用しない場合.
else:
return frame_trans_global(self.rot,
self.inertia_moment * self.dot_w +\
np.cross(self.w, self.inertia_moment * self.w)) -\
np.cross(self.p - self.cg, self.force)のように計算する.これは前述の慣性力と力のモーメントを計算する関数Inertial_Force_global()とJoint_Moment_global()をあわせただけである.
この計算結果は,同様に,クラスBodyLinkのインスタンス変数としてself.tau_globalを準備し,再帰呼び出しによって関節に作用するトルクを計算するメソッド関数ID_Euler()の
j_moment_global = self.Joint_Moment_global()
self.j_moment_global = j_moment_globalで,インスタンス変数self.tau_globalに代入し,関数ID_Euler()は最終的にこれを出力する.
なお,関節に作用するトルクの計算には,二分木の兄弟姉妹(sister_val)を加算せずに,子供の部位のトルクだけ加算したいので,sister=True等の全身計算では
tau_global = self.Torque() + self.child_val.ID_Euler(sister)
tau_global_sister = tau_global + self.sister_val.ID_Euler(sister)
self.tau_global = tau_global
return tau_global_sisterのように再帰呼び出しでは,tau_global_sisterを返して,すべての部位(link)をたどるようにしているが(訂正前と同じ),その部位のトルクを格納しているself.tau_global には tau_global(子供のリンクchild_valのトルク)だけ代入している.
床反力(地面反力)
これまでのコードに変更を加えて,全身の系に対する外力,すなわちこここではフォースプレートで計測した並進力と力のモーメントを,クラスBodyLinkのインスタンス変数としてext_forceとext_momentを準備し,それらが作用する右足b_link[12]と左足b_link[15]に対して,
b_link[12].ext_force = fp2op_frame(file_path_fp_12, file_path_op_12, 2, 'f')
b_link[15].ext_force = None # fp2op_frame(file_path_fp_12, file_path_op_12, 1, 'f')
b_link[12].ext_moment = moment2link(file_path_fp_12, file_path_op_12, 12)
b_link[15].ext_moment = None #moment2link(file_path_fp_12, file_path_op_12, 15)のように格納した.ただし,この踏み台から右足で飛び降りる試技に関しては,右足にしか実際には力が作用していないので,左足に床反力データは与えていない(Noneとした).
関数ID_Euler()のコードでは,もしself.ext_momentが空(None)出ない場合は,
if np.any(self.ext_moment) != Noneでチェックし,それらを外力として計算するコードとしている.
なお,平行軸の定理を利用し,フォースプレートの力のモーメントを末端のlinkである足部の力のモーメントに変換する関数moment2link()において,変換する力のモーメントの原点に誤りがあった(末端のlinkの原点 → linkの重心).
# (★ 221221訂正)linkの原点 → linkの重心
# force plateのモーメントをlink(link_idで指定)の重心まわりのモーメントに変換
# 正確にはlink_idの遠位側(distal_val)に作用する力
# fp_x_size = .6 # force plateのx方向の大きさ [mm]
# fp_y_size = .9 # force plateのy方向の大きさ [mm]
# fp_z_origin = -.045 force plateの原点の方向成分
def moment2link(file_path_fp, file_path_op, link_id, sf_original=1000., sf_new=360., fp_x_size=.6, fp_y_size = .9, fp_z_origin=-.045):
op = extract_marker(file_path_op, 'RHand') # motion captureデータ:右手データを使用(何でも良い)
len_op = len(op) # モーションキャプチャのデータの長さ
if link_id == 12:
fp_num = 2
fp_origin = [-fp_x_size/2., fp_y_size/2., fp_z_origin] # motion captureの原点座標
elif link_id == 15:
fp_num = 1
fp_origin = [fp_x_size/2., fp_y_size/2., fp_z_origin]
moment_fp_frame = fp2op_frame(file_path_fp, file_path_op, fp_num, 'm', sf_original, sf_new)
moment_link_frame = np.cross(fp_origin - b_link[link_id].cg, b_link[link_id].ext_force) + moment_fp_frame # (★ 221221訂正)
return moment_link_frame補足
補足1:それでもバターワースフィルタを使いますか?
ここでは,ニュートンの運動方程式になるが,平滑化スプラインの性能を改めて確認する.
全身の並進の力学を考えると,
$$
\sum_{i=1}^{n} (m_i (\ddot{\bm{x}}_{gi} - \bm{g})) = \bm{F} \\
M(\ddot{\bm{X}}_{G} - \bm{g}) = \bm{F}
$$
となる.ここで,$${m_i}$$は身体の部位$${i}$$の質量,$${\bm{x}_{gi}}$$は部位$${i}$$の重心の位置ベクトル,$${\bm{g}}$$は重力加速度,$${\bm{F}}$$は床反力,$${M=\sum_{i=1}^n m_i}$$は全身の質量(体重),$${\bm{X}_{G}}$$は身体重心の位置ベクトルである.
合成重心のメソッド関数Resultant_Cg()については
を参照されたい.
この式は,身体重心の加速度$${\ddot{\bm{X}}_{G}}$$を計算し,さらに$${M(\ddot{\bm{X}}_{G} - \bm{g})}$$を与えれば,それは床反力$${\bm{F}}$$と一致することを示している.面倒だが床反力は,フォースプレートがなくても推定できることを意味する.
このことを改めて計算し,どの程度,違いがあるか見てみよう.
まず,床反力$${\bm{F}}$$を以下のコード
m = 86.
force_cg = m * (smoothing_spline(b_link[1].Resultant_Cg(m, True), .00001, 360, order=2)-[0,0,-9.8])
t_list = np.arange(len(force_cg))/360.
[plt.plot(t_list, force_cg[:,i], linestyle = '--', c=['b','orange','g'][i]) for i in range(3)]
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])で確認すると,
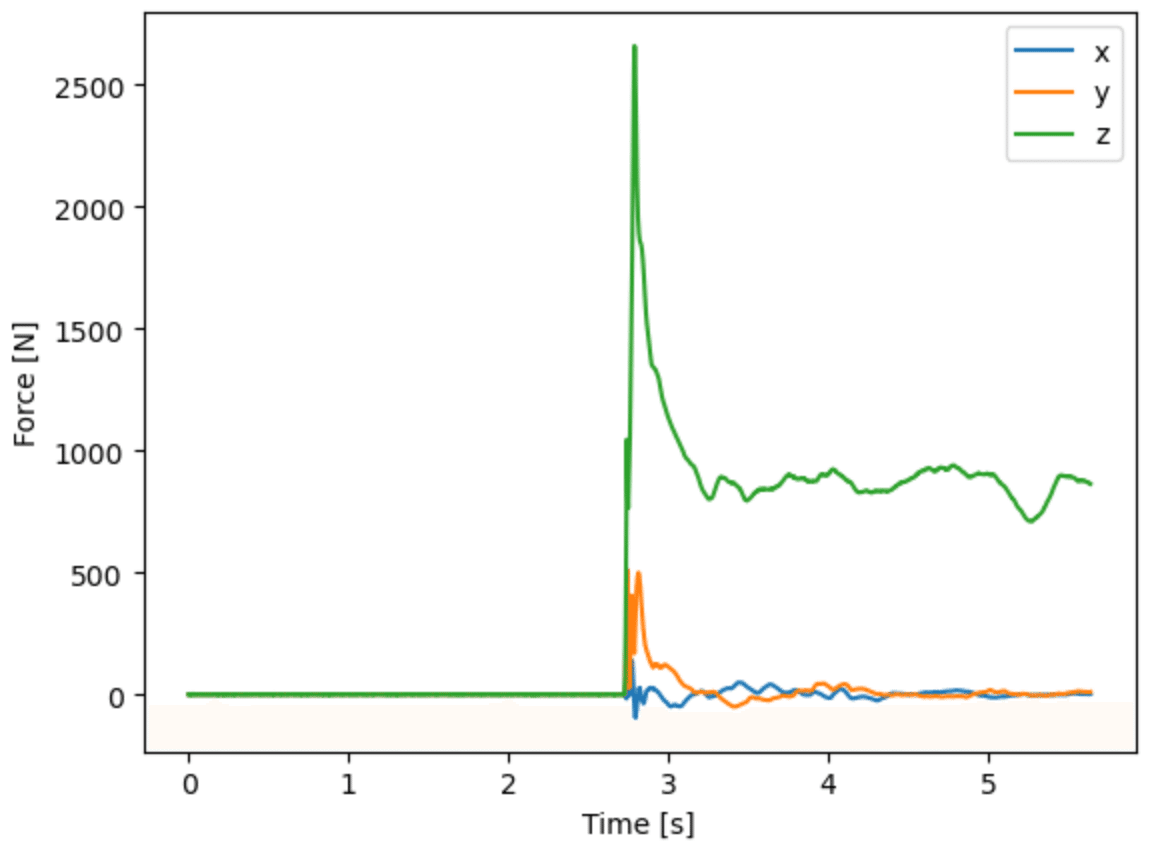
のようになる.次に,
b_link[1].ID_Newton(86., True)のように全身の並進の力学計算を行い,その後に,以下のコードのように,メソッドResultant_Cg()が重心を再帰呼び出しで計算する関数なので,b_link[1].Resultant_Cg(m, True)によって全身の重心を計算し,それをsmoothing_spline()によって重心の加速度を計算し,$${M(\ddot{\bm{X}}_{G} - \bm{g})}$$を計算する.
m = 86.
force_cg = m * (smoothing_spline(b_link[1].Resultant_Cg(m, True), .00001, 360, order=2)-[0,0,-9.8])
t_list = np.arange(len(force_cg))/360.
[plt.plot(t_list, force_cg[:,i], linestyle = '--', c=['b','orange','g'][i]) for i in range(3)]
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])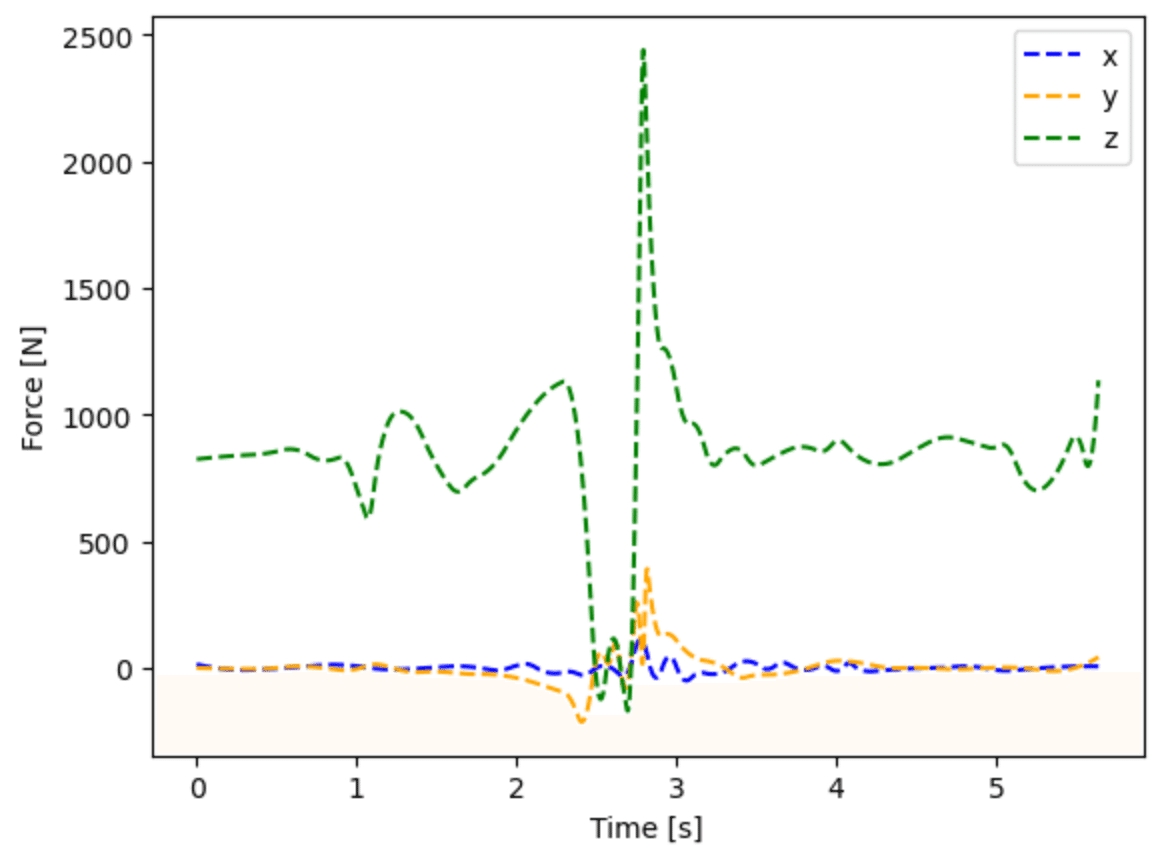
この計算では2.5 [s]前後で空中に跳んでいる.フォースプレートのデータでは,その前に力は作用しないが,身体重心から計算する外力では,左右の床反力の総和に相当する力が計算されている.
さて,これらを比較してみよう.
m = 86.
force_cg = m * (smoothing_spline(b_link[1].Resultant_Cg(m, True), .00001, 360, order=2)-[0,0,-9.8])
t_list = np.arange(len(force_cg))/360.
plt.plot(t_list, b_link[12].ext_force)
[plt.plot(t_list, force_cg[:,i], linestyle = '--', c=['b','orange','g'][i]) for i in range(3)]
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z','x', 'y', 'z'])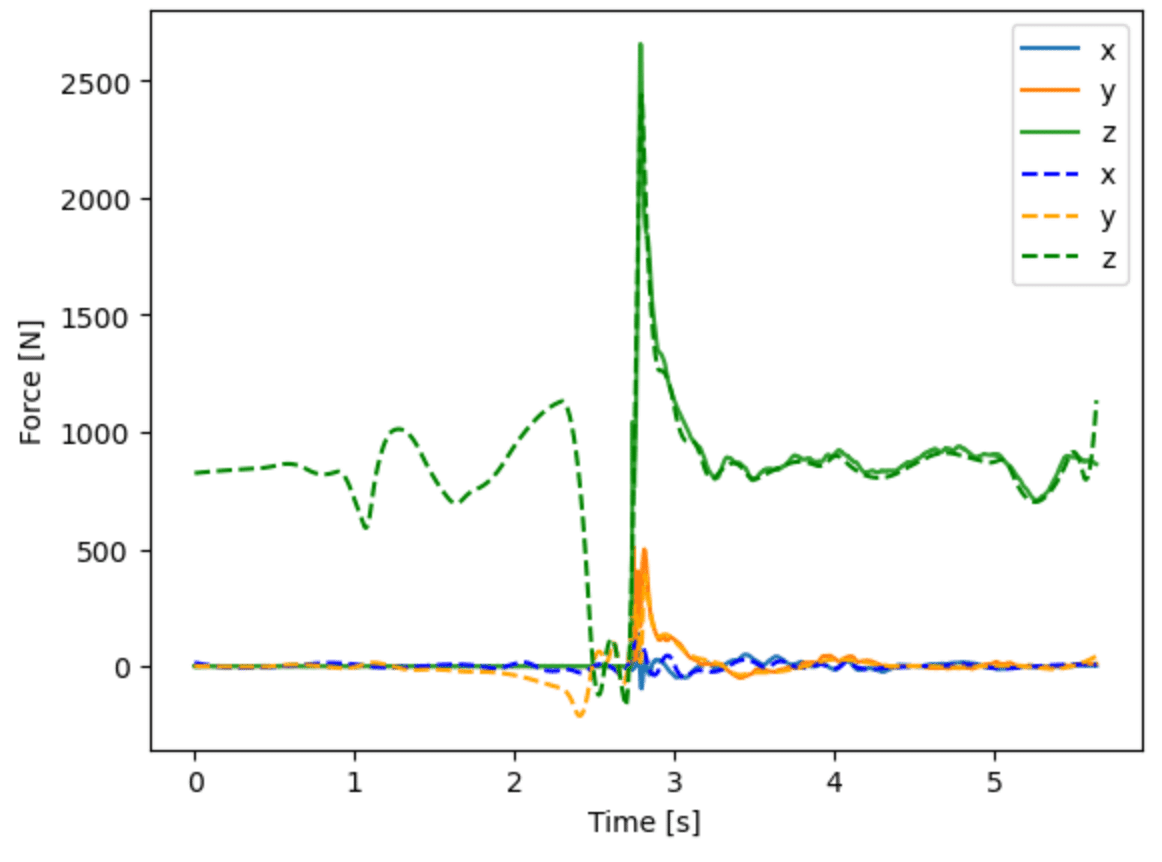
これらの一致具合は,かなり高い.15個の身体の各部位から重心を計算し,その加速度を計算しても,かなり精度良く床反力を推定できることをこの例は示している.
これはバターワースフィルタでは,実現が難しいだろう.ご自身でフィルタの性能を比較されてみてはいかがだろう.
補足2:それでもCOPを使いますか?
で述べたが,平行軸の定理で座標変換したフォースプレートの力のモーメントを,2つの方法で計算し比較する.
フォースプレートは4つの力覚センサによって,直接的には3軸の並進力を計測する計測機器である.そこから,フォースプレートに作用するモーメントも2次的に計算し出力する.
フォースプレートは基本的には,この「並進力のベクトル」と「フォースプレート座標系の原点まわりの力のモーメントベクトル」を出力する計測機器である.
そして,
では,さらに,それらは平行軸の定理(力のモーメントの座標変換)によって,COPに作用する力と摩擦モーメント(フリーモーメント)に置き換えることができることをで示した.
すなわち,「フォースプレート座標系の原点まわりの」力のモーメントとして与えられる力のモーメントが,「COPまわりの」力のモーメントに(座標)変換すると,水平軸まわりの力のモーメントが0となり,鉛直軸まわりの摩擦によって生成される力のモーメントだけになることを意味し,これは前述の「フォースプレート座標系の原点まわりの力のモーメントベクトル」と原点が異なるだけで,それらは等価で,原点を移動し変換した同じ力のモーメントである.
ひょっとすると,ここで一部の方は,この便利な(わかりやすい)性質を利用し,COPに作用する力と摩擦モーメントによって,「足部の重心まわり」に作用する力のモーメントを計算してはいないだろうか.
もちろん,これは間違いではない.ただし,これは計算効率や精度上好ましくない方法である.
理由は単純である,もし,力のモーメントに関する平行軸の定理を正しく理解できているなら,この計算は二度手間であることがわかるだろう.フォースプレート座標系から足の座標系に変換するために,わざわざCOPまわりの力のモーメントを経由(計算)し,足の原点まわりのそれに変換する必要はない.
「フォースプレート座標系の原点まわりの」力のモーメントは,COPまわりの力のモーメントを経由せず,直接「足部の重心まわりの」力のモーメントに変換すればよいだけのことだ.
ここでは,この余計な計算は,「数値的に誤差を発生する要因となる」ことを示したい.
COPは以下の式で計算される,
$$
p_x = \frac{-M_{sy}+c F_{x}}{F_{z}}\\ p_y =\frac{M_{sx}+c F_{y}}{F_{z}}
$$
ここで,$${p_x, p_y}$$はこのCOPの$${x,y}$$座標,$${c}$$は原点$${\text{S}}$$とフォースプレート表面までの鉛直方向の距離パラメータ,$${\bm{F}=[F_x~F_y~F_z]^T}$$は床反力ベクトル,$${\bm{M}_s = [M_{sx}~M_{sy}~M_{sz}]^T}$$をフォースプレート座標系の原点まわりの力のモーメントベクトルである.
ここで,注目していただきたいのは,この計算には鉛直方向の床反力$${F_{z}}$$による除算を含んでいる.もし,この$${F_{z}}$$の値が小さい場合は,誤差を生じやすい.
には,この計算過程を詳細に示したが,ここでは,この二つの計算方法による比較の結果だけを示す.
以下の図4は,前者のCOPの位置ベクトル$${\bm{p}_s}$$を利用し
$$
(\bm{p}_s - \bm{x}_{g12}) \times \bm{F} + \bm{\tau}(\bm{p}_s)
$$
から計算した(二度手間の方法,実線),右足の重心$${\bm{x}_{g12}}$$まわりの力のモーメントベクトルと,前述のフォースプレートの原点まわりの力のモーメントを直接,足関節の原点$${\bm{x}_{g12}}$$まわりの力のモーメントベクトルへ変換した場合(破線)の比較図である.ここで,$${\bm{\tau}(\bm{p}_s)}$$は鉛直軸まわりの摩擦モーメントベクトルである.
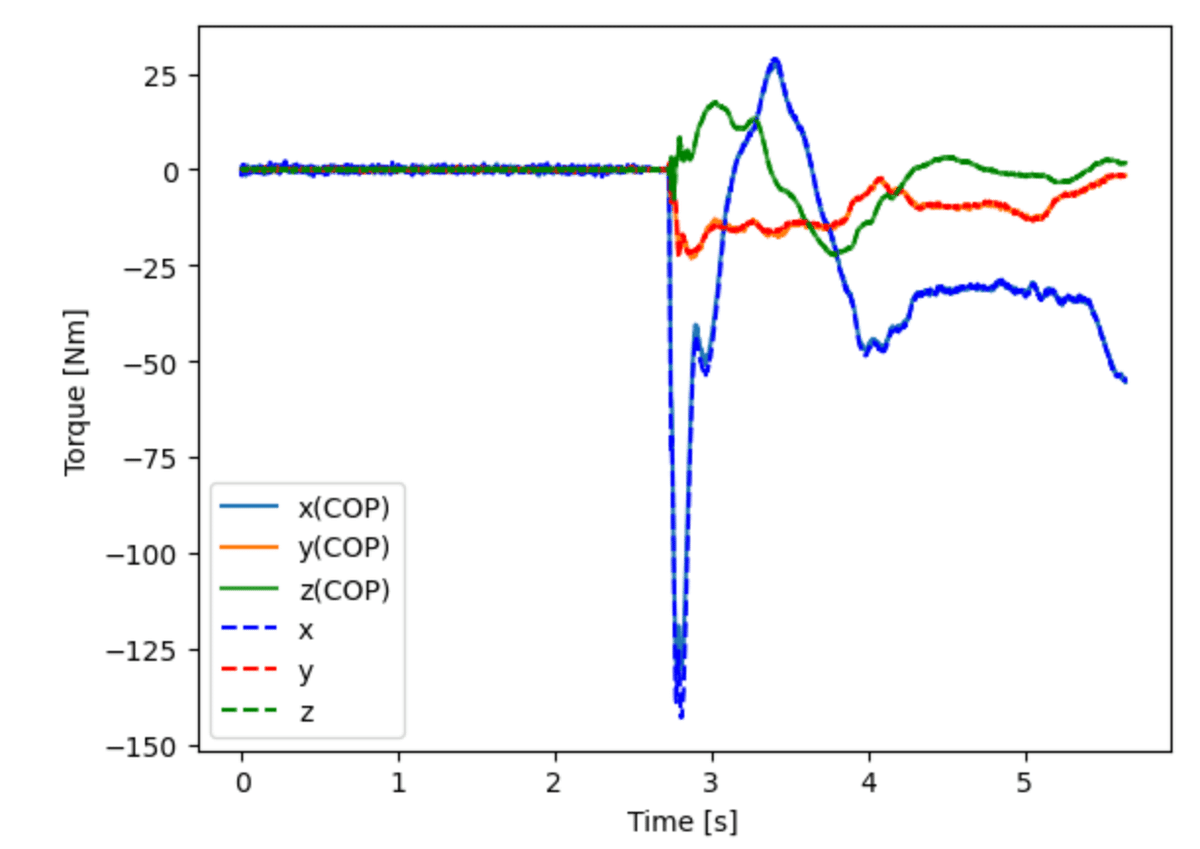
図4は,実線は前者のCOPを利用した計算方法による結果で,破線はフォースプレート座標系から足関節の原点まわりに変換した結果である.
これらはよく一致しているようだが,これらの差分を計算すると
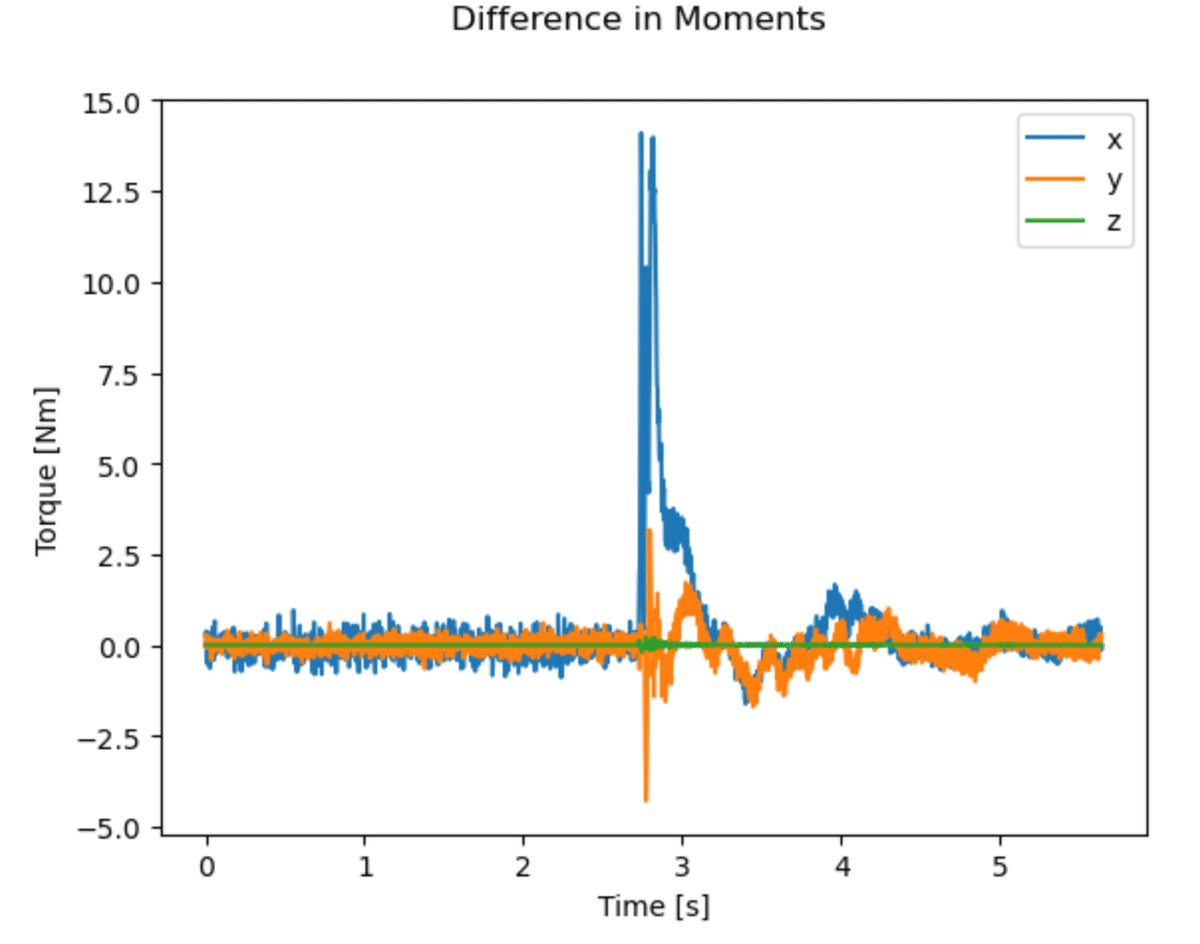
のようになる.前述のように作用する力が小さい時,除算によって暴れている様子が$${x, y}$$の力のモーメントに現れている.鉛直軸まわりは除算がないため,大きな違いはない.この差が大きいか小さいは読者の判断に任せよう.
最後に
これ以外の計算例も少しばかりであるが,
に示したので,ご覧になっていただければと思う.
とりあえず,関節に作用するトルクを計算するコードを示し,この章の一区切りを迎えたが,単にトルクを計算することが目的ではなく,力学計算を通して,身体の運動におけるトルクなどの物理的意味を理解することが重要である.
そこで,今後,これらのコードを活用したり,力学的エネルギーの時間変化(パワー)やスティックピクチャを描くコードなど,述べていきたい.
次章
では,ここで用いた再帰呼び出しによる解法ではなく,合成の回転の運動方程式を導出し,身体運動における関節作用するトルクの物理的意味を考えていきたい.


【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
