
動かして学ぶバイオメカニクス#11 〜全身のオイラーの運動方程式〜
このシリーズので目標は,関節に作用するトルクを計算することであったが,この章で,オイラーの運動方程式を解きニュートン・オイラー法で並進力と回転力を計算する準備が整う.ここでは,フォースプレートによる外力の計測も考慮し,身体の多関節構造を考えた全身の回転の運動方程式を完成させる.
オイラーの運動方程式の慣性力の計算
多関節構造を持つ,多体系の運動方程式(マルチボディダイナミクス)を解く際,計測環境などによって計算方法を適切に考える必要がある.ここでは,フォースプレートとモーションキャプチャで計測することを意識し,全身で関節に作用するトルクを計算する運動方程式の立て方を考える.
解析力学で扱われるラグランジュの運動方程式は,最小限の変数で運動を記述する方法で,ある意味,見通しが良い記述方法だ.一方,ニュートンの運動方程式とオイラーの運動方程式の組み合わせは,冗長である意味,無駄な変数が登場する.
また,これらの式は記述が全く異なるが,同じ対象を記述する運動方程式であるならば,あたりまえだが同じ解を導く.物理や工学系ではラグランジュの運動方程式で記述することが好まれる傾向にあるが,身体運動の物理的意味を問う解析を行う上では,また計算効率を考えると,ニュートン・オイラー法(Newton-Euler method)が適切なときもある.
しかし,身体運動において,このラグランジュの運動方程式には表れない「無駄」が身体にとっては大きな意味を持つことがある.たとえばラグランジュの運動方程式には表れない,関節と関節間に作用する作用反作用の力は,ラグランジュの運動方程式では無駄な変数でも,身体にとっては関節を通して,力学的エネルギーを伝達する媒介となっている.これを可視化し観察することは,身体運動の解析にとっては意味がある.むしろ見えてこないと困る「力」である.
そこでここでは,全身の関節に作用する並進力とトルクを計算する逆動力学計算を行うために,ニュートン・オイラー法(Newton-Euler method)を使用するが,一般的にロボティクスで計算する手順とヒトの計算では,計測環境や身体のモデルが若干異なるため修正が必要である.多くのバイオメカイクスの教科書でも基本的な式が取り上げられているが,ここではアルゴリズム(再帰呼び出し),計測方法,さらには物理的意味を意識し,その方法をより明示的に述べる.本章で述べる運動方程式レベルでは違いがあまりないが,次章で述べる予定のコードに置き換える時点では,再帰呼び出しのアルゴリズムで違いが浮き彫りになる.再帰呼び出しにこだわる必要はないが,コードの間違いを減らし,何よりも運動方程式の物理的意味を考えていく上で大いに利点があると考えている.
オイラーの運動方程式の復習
一つの部位を構成する基本的なオイラーの運動方程式は,すでに第7章
で導出した.これは,ニュートンの運動方程式の回転バージョンと思えば良い.運動量の時間微分によってニュートンの運動方程式を導出したように,角運動量を時間微分することで,オイラーの運動方程式を導出している.そして,それは慣性力と外力である力のモーメントやトルクの項で構成される.
ここでは,上腕などの一つの剛体(部位)に関する運動方程式ではなく,各身体部位の総和である身体全体のオイラーの運動方程式の立て方について考えていく.
角速度の復習
前章
では,角速度の計算方法について述べた.最終的には座標系に固定された基底ベクトル(単位ベクトル)の微分とそれと直交する基底ベクトルとの内積で計算される.
簡単に振り返ると,速度と角速度の関係
$$
\dot{\bm{r}} = \bm{\omega} \times \bm{r}
$$
の関係から,外積についての除法が成り立たないので,速度ベクトル$${\dot{\bm{r}}}$$が得られても角速度ベクトル$${\bm{\omega}}$$を計算できない.しかし,姿勢回転行列を構成する座標軸に固定された直交する3つの単位ベクトル(基底ベクトル)のついても同じ式が成り立つため,この3つの各基底ベクトルの速度がわかれば,直交条件とともに角速度を計算できる.
オイラーの運動方程式における慣性力
このようにして得られた身体各部位の角速度ベクトル$${\bm{\omega}}$$と,慣性テンソル$${\bm{I}}$$から,オイラーの運動方程式における慣性力
$$
\bm{I} \dot{\bm{\omega}} + \bm{\omega} \times (\bm{I} \bm{\omega})
$$
を計算する.なお,通常慣性テンソルは重心まわりの慣性テンソルで身体各部位に固定された座標系で記述すれば一定値の対角行列で計算できるので,それに合わせて角速度ベクトルも身体に固定されたローカル座標系で計算し,慣性力もローカル座標系で計算したうえで,外力の計算も含めた最後の計算で絶対座標系に変換するのが良い.
オイラーの運動方程式の外力の計算
ここで,第4章
のニュートンの運動方程式で扱った身体構造の具体例を再び取り上げ,重心まわりのオイラーの運動方程式を記述し,漸化的にオイラーの運動方程式を解くことを意識しながら運動方程式を構成する..
ニュートンの運動方程式では再帰計算による結果が「系の合成の並進の運動方程式」になることを示した.同様にオイラーの運動方程式についても再帰計算の結果,それが「系の合成の回転の運動方程式」になる.
これから示すオイラーの運動方程式の再帰計算の過程では,運動方程式にリンク間の関節に作用する並進力が媒介し,これまで述べたニュートンの運動方程式による関節に作用する並進力の計算結果を利用する.したがって,一見するとこの並進力がリンク全体の運動方程式からも消えないため,合成の運動方程式からは内力が
消えないと考えがちだが,実はオイラーの方程式でも内力は相殺され消える.これは,系にとって系内部の関節間に作用する並進力は内力であるためで,並進の運動方程式と同様,結果的には系全体の回転の運動方程式からも,関節間に作用する力とトルクが相殺される運命にある.実際,ラグランジュの運動方程式で記述すれば,関節に作用する並進力は現れない.
そして,運動方程式から内力が消えてしまえば,トルクの大小の議論ではなく,たとえば「どのような理由でそれが大きくなるのか」,「どのような理由でそれを大きくしないといけないのか」という,関節に作用するトルクの物理的意味が明確になる.ただし,関節に作用する並進力は,いつも見えないほうがよいとは限らない.身体運動では重要な役割を果たすため,その物理的意味を考える上では明示的に示したほうが良いときもある.このことについては,別途述べていく.
多体系のオイラーの運動方程式
以下に,ニュートン・オイラー法(文献1)によって運動方程式を誘導するための手順を説明する.図1に示すように,第4章で示したモデルを例に取り上げる.
運動学
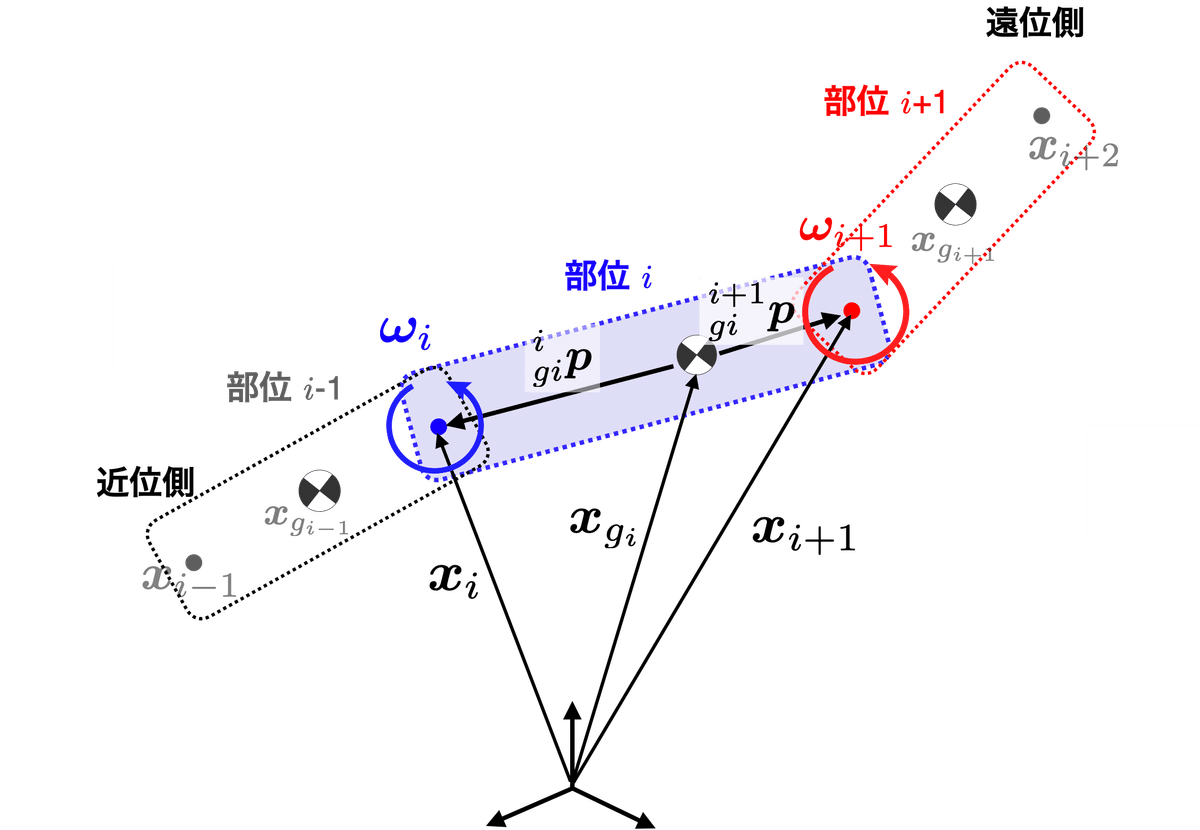
これまでの計算で,各部位(リンク)$${i}$$の原点,すなわち近位側の関節の位置ベクトル$${\bm{x}_i}$$, 各部位$${i}$$の重心の位置ベクトル$${\bm{x}_{gi}}$$はモーションキャプチャのデータと統計モデルから計算され,コードにおいてクラスBodyLinkのインスタンス変数pとcgに代入されている.さらにそれらを二階微分した$${\ddot{\bm{x}}_{gi}}$$をインスタンス変数accに格納する.
またこれを利用し,部位$${i}$$の重心$${\bm{x}_{gi}}$$からみた関節(部位$${i}$$の原点)$${\bm{x}_{i}}$$の位置ベクトルを$${{}_{gi}^{i}\bm{p} = \bm{x}_{i} - \bm{x}_{g1}}$$,$${\bm{x}_{gi}}$$からみた関節(部位$${i+1}$$の原点)$${\bm{x}_{i+1}}$$の位置ベクトルを$${~{}_{gi}^{i+1}\bm{p} = \bm{x}_{i+1} - \bm{x}_{g1}}$$とする.
また,前章で述べた,部位$${i}$$の角速度ベクトル$${\bm{\omega}_i}$$はインスタンス変数wに,さらにその時間微分の角加速度ベクトル$${\dot{\bm{\omega}}_i}$$はdot_wに格納する.これで,ニュートン・オイラー法の計算に必要な運動学データが揃う.
オイラーの運動方程式における外力
各部位$${i}$$の角速度$${\bm{\omega}_i}$$で記述される運動を行うために加えられる回転力を,オイラーの運動方程式から算出する.なお,オイラーの運動方程式における外力を方程式の右辺に列挙する.
ここので外力としての回転力は,遠位の部位を除いて一つの部位に対して二つの関節が存在するため,筋力が生成する各関節に作用するトルクが二つ,関節に作用する力が生成する力のモーメントが二つ作用する.ここでは,重心まわりの運動方程式を考えるため,重力による力のモーメントは無視できる.
なお,ここで述べる関節に作用するトルクは偶力と同様に,原点に依存しない回転力である.力のモーメントは,回転軸(原点)に依存するので注意されたい.
力のモーメントについては
も参照されたい.

通常のニュートン・オイラー法では,リンク毎に力とモーメントの両方を計算するのが一般的であるが,ここでは再帰呼び出しのコードを活用するためオイラーの運動方程式を計算する前に,ニュートンの運動方程式で並進力の計算を先にすませる.
計算した並進力$${\bm{f}_i}$$については,第6章
のコードでインスタンス変数forceに格納しておく.
以上の説明を,以下に具体的に式で表現する.
部位$${i}$$に対しては,部位(リンク)$${i}$$の関節の原点$${\bm{x}_i}$$にトルク$${\bm{\tau}_i}$$が作用し,遠位側の部位$${i+1}$$の原点$${\bm{x}_{i+1}}$$に作用するトルク$${\bm{\tau}_{i+1}}$$の反作用$${-\bm{\tau}_{i+1}}$$が作用する(図1,2参照).
同様に部位$${i}$$に対して,$${\bm{x}_i}$$に力$${\bm{f}_i}$$が作用し,$${\bm{x}_{i+1}}$$に反作用の力$${-\bm{f}_{i+1}}$$が作用し,さらに重心$${\bm{x}_{gi}}$$には鉛直下方に重力$${m_i \bm{g}}$$が作用し,これらが力のモーメントを生成する.なお関節に作用する力は,第4章のニュートンの運動方程式で計算された力(前述のように,これまで示したクラスBodyLinkのforce)を利用する.
力のモーメントの計算
前述のように.各部位$${i}$$には外力として,原点(近位側の関節)$${\bm{x}_i}$$に$${\bm{f}_{i}}$$が,遠位側の関節$${\bm{x}_{i+1}}$$に$${-\bm{f}_{i+1}}$$が,重心$${\bm{x}_{gi}}$$には重力$${m_i \bm{g}}$$が作用する.
すると,各部位$${i}$$には「重心$${\bm{x}_{gi}}$$まわり」の力のモーメントとして,
$$
{}_{gi}^{i}\bm{p} \times \bm{f}_{i} + {}_{gi}^{i+1}\bm{p} \times (-\bm{f}_{i+1})
$$
が作用する.ここで,重心$${\bm{x}_{gi}}$$から見た各関節の位置ベクトルを$${{}_{gi}^{i}\bm{p}, {}_{gi}^{i+1}\bm{p}}$$とした.なお,重力は重心に作用すると考え,重力による力のモーメントは$${0}$$となる.
なおロボティクスでは,さらに並進の運動方程式
$$
m_i \ddot{\bm{x}}_{gi} = m_i \bm{g} + \bm{f}_i - \bm{f}_{i+1}
\\
\bm{f}_i = m_i (\ddot{\bm{x}}_{gi} - \bm{g}) + \bm{f}_{i+1}
$$
を利用し,これを重心まわりに作用する力のモーメント
$$
{}_{gi}^{i}\bm{p} \times \bm{f}_{i}
+
{}_{gi}^{i+1}\bm{p} \times (-\bm{f}_{i+1})
$$
に代入することで,
$$
{}_{gi}^{i}\bm{p} \times (m_i \ddot{\bm{x}}_{gi} + \bm{f}_{i+1})
+
{}_{gi}^{i+1}\bm{p} \times (-\bm{f}_{i+1})
\\
= {}_{gi}^{i}\bm{p} \times (\bm{f}_{i+1})
+
{}_{gi}^{i+1}\bm{p} \times (-\bm{f}_{i+1})
+
{}_{gi}^{i}\bm{p} \times m_i (\ddot{\bm{x}}_{gi} - \bm{g})
\\
= ({}_{gi}^{i}\bm{p} - {}_{gi}^{i+1}\bm{p}) \times (\bm{f}_{i+1})
+
{}_{gi}^{i}\bm{p} \times m_i (\ddot{\bm{x}}_{gi} - \bm{g})\\
= {}_{i}^{i+1}\bm{p}\times (\bm{f}_{i+1})
-
{}_{i}^{gi}\bm{p} \times m_i (\ddot{\bm{x}}_{gi} - \bm{g})\\
$$

のように,各部位の原点まわりのモーメントの式に書き換えて計算することが多い(文献1).ここで,$${{}_{i}^{gi}\bm{p}}$$は部位$${i}$$の原点$${\bm{x}_i}$$から$${\bm{x}_{gi}}$$への位置ベクトル,$${{}_{i}^{i+1}\bm{p}}$$は原点$${\bm{x}_i}$$から遠位の部位$${i+1}$$の原点$${\bm{x}_{i+1}}$$への位置ベクトルである(図3).
一方,バイオメカニクスのようにモーションキャプチャで計測したデータから力学計算を行うときには,違いは少なくどちらの式を使用しても構わない.ここでは,若干コードの記述が少ない重心(質量中心)まわりの力のモーメントを採用する.ただし,この原点まわりの力のモーメントへの変換方法は,合成の運動方程式を考えてく際に重要となる.
もし,ローカル座標系で計測するモーションセンサを利用する際にはロボットのように計算するのが良いだろう.しかし,モーションキャプチャを利用した解析では,力や力のモーメントはモーションキャプチャの座標系のままの計算のほうが,座標変換を部分的に行う必要がなく有利なので,ここでは力のモーメントの計算は絶対座標系で計算する.
慣性力の計算
慣性テンソルは各部位に固定された座標系で計算するほうが,姿勢によって変化することなく一定値となり有利である.したがって,ここでは慣性力も,$${\bm{I}_i^i \dot{\bm{\omega}}_i^i + \bm{\omega}_i^i \times (\bm{I}_i^i \bm{\omega}_i^i)}$$のように,まずローカル座標系で計算し,その後に絶対座標系に変換する.ここで,新たな記号の表記方法を示しているが,右上の上付きの記号$${i}$$は記述している座標系を示している.一般論を議論する際には,これまで記述してきたように,そもそも座標系に依存しない式であったため,座標系を考えない数理表現のほうが都合が良いが,計測や成分の計算を意識する最終的な段階では,このような表記が必要となる.
オイラーの運動方程式
以上から,部位$${i}$$のオイラーの運動方程式
$$
\bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i) = {}_{gi}^{i}\bm{p} \times \bm{f}_{i} - {}_{gi}^{i+1}\bm{p} \times \bm{f}_{i+1} + \bm{\tau}_i - \bm{\tau}_{i+1}
$$
を得る.この式は,座標系に依存しない形で書かれている.
次に示すように,この式の左辺の慣性力はローカル座標系で計算され,右辺の外力は絶対座標系で計算されるが,左辺の慣性力は姿勢回転行列rotを利用し絶対座標系に座標変換し,再帰呼び出しによって計算する.
漸化式(再帰呼び出し)による,オイラーの運動方程式の解法
以上の結果を利用すると,
$$
\bm{\tau}_i = \bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i) + \left(-{}_{gi}^{i}\bm{p} \times \bm{f}_{i} + {}_{gi}^{i+1}\bm{p} \times \bm{f}_{i+1} \right) + \bm{\tau}_{i+1}
$$
のように部位$${i}$$に作用するトルク$${\bm{\tau}_i}$$と書き換えることができる.この式は,漸化式となり,プログラムでは,右辺の$${\bm{\tau}_{i+1}}$$が,次の部位のトルクの式
$$
\bm{\tau}_{i+1} = \bm{I}_{i+1} \dot{\bm{\omega}}_{i+1} + \bm{\omega}_{i+1} \times (\bm{I}_{i+1} \bm{\omega}_{i+1}) + \\
~~~~~~~~~~~~~~~\left( -{}_{g~i+1}^{i+1}\bm{p} \times \bm{f}_{i+1} + {}_{g~i+1}^{i+2}\bm{p} \times \bm{f}_{i+2} \right) + \bm{\tau}_{i+2}
$$
では,さらに遠位の部位$${i+2}$$の関節に作用するトルク$${\bm{\tau}_{i+2}}$$を呼び出すことになり,ニュートンの運動方程式と同様に,オイラーの運動方程式の解放のアルゴリズムにおいても再帰呼び出しの構造となることを予想させる.実際のコードでは,この式を再帰呼び出しで実装すれば良い.
また,これを末端の部位$${n}$$まで加算すると,系内の関節間に作用するトルクが打ち消され,ニュートンの運動方程式における再帰計算で示したように,最終的にアルゴリズムは内部で勝手に
$$
\bm{\tau}_i = \sum_{i}^n \left(\bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i) \right) + \sum_{i}^n \left(-{}_{gi}^{i}\bm{p} \times \bm{f}_{i} + {}_{gi}^{i+1}\bm{p} \times \bm{f}_{i+1} \right)
$$
を計算することになる.これは,ニュートンの運動方程式の再帰呼び出しと同様な計算方法となり,他の関節に作用するトルクが全て消え,ニュートンの運動方程式の再帰呼び出しと同様な計算方法となっていることが式の上からも示された(補足1).
なお,前述のように慣性力は身体に固定された座標系で計算するので,絶対座標系に変換する.それ以外の外力項は,絶対座標系で計算する.このことを意識し,以下では記号の右上に座標系を明示し,絶対座標系で記述した部位$${i}$$の関節に作用するトルク$${\bm{\tau}_i^0}$$は
$$
\bm{\tau}_i^0 = \sum_{i}^n {}^0\bm{R}_i\left(\bm{I}_i ^i \dot{\bm{\omega}}_i^i+ \bm{\omega}_i^i \times (\bm{I}_i^i \bm{\omega}_i^i) \right) + \sum_{i}^n \left(-{}_{gi}^{i}\bm{p}^0 \times \bm{f}_{i}^0 + {}_{gi}^{i+1}\bm{p}^0 \times \bm{f}_{i+1}^0 \right)
$$
と書くことができる.ここで,右上付きの記号は座標系を意味し,たとえば$${0}$$は絶対座標系(たとえばモーションキャプチャ座標系でよい)を意味し,$${{}^0\bm{R}_i}$$は座標系$${i}$$から絶対座標系$${0}$$への座標変換行列を意味する.
なお,どちらかというと一般的な方法の再帰呼び出しを使用しない場合は,末端の部位から近位に向かて逐次解けば良い.式の違いはわずかであるので読者の練習問題として残し,ここでは示さない.その場合,コードに記述する際には,身体の構造によって,どこからどこまで計算するかなどを,if文のような場合分けが必要となるだろう.しかし,見かけ上,近位から遠位に向かって解く再帰呼び出しではこのような記述は不要である.これも二分木による再帰呼び出しで記述する利点である.ただし,二分木に(コードではクラスの親子,姉妹関係に)if文の役割を埋め込んでいるだけとも言えるので好みの問題とも言える.
床反力による力のモーメント
足部が地面と接触する場合,足部には床反力(地面反力)による力のモーメントが作用する.その場合,その地面から受け取る力のモーメントも足部に加える.
第6章でオイラーの運動方程式を解く際に,足部に作用する床反力は,フォースプレート座標系からモーションキャプチャ座標系(絶対座標系)への回転の座標変換を行えばよかった.しかし,モーメントの座標変換は,さらに平行軸の定理に従った変換を行う必要があり回転の座標変換だけでは不十分である.力のモーメントを含めて,全てのモーメント(角運動量や慣性モーメントなども含めて)は原点(回転の中心)に依存して値が変化する物理量であるという性質を思い出してほしい.力のモーメントの平行軸の定理については
を参照されたい.ここでは,フォーズプレート座標系から足部の座標系の原点への力のモーメントへの変換が必要となる.なお,この計算は回転行列が一定値となるので絶対座標系で変換を行うほうが容易である.
また,フォースプレートに作用する力のモーメントの足部への座標変換は,COPと摩擦モーメント(フリーモーメント)を通して力のモーメントを計算することと等価であるが,COPが除算によって計算されていることに起因する精度の劣化と,余計な計算を行っていることを考慮すると,フォースプレートの力のモーメントから平行軸の定理によって座標変換するほうが望ましい.
図4の例で,具体的に考える.

今,フォースプレート座標系Sで計測される力のモーメント,すなわち足部とフォースプレート間に作用する力のモーメント$${\bm{M}(S)}$$を,足部座標系fから見た力のモーメント$${\bm{M}(f)}$$に,平行軸の定理を用いて変換することを考える.フォースプレートからは力$${\bm{F}}$$も計測されている.
また,足部座標系fの原点から見た,フォースプレート座標系Sの原点への位置ベクトルを$${{}^S_f \bm{p}}$$とする.
前述のように,フォースプレートで計測される力$${\bm{F}}$$と力のモーメント$${\bm{M}(S)}$$は,平行軸の定理によって座標系の原点をCOP(圧力中心)$${\bm{p}_s}$$に作用する力$${\bm{F}}$$と鉛直軸まわりの力のモーメント$${\bm{\tau}(\bm{p}_s)}$$に座標変換することができ,これらを利用して足部の原点$${f}$$まわりの力のモーメント$${\bm{M}(S)}$$
$$
\bm{M}(f) = ({}^S_f \bm{p} + \bm{p}_S) \times \bm{F} + \bm{\tau}(\bm{p}_s)
$$
として計算することができるが,この計算は先程述べたように,余分な計算を増やし精度を劣化させるだけなので行わないのが懸命である.
そこで,同様に平行軸の定理を用いて,「フォースプレートの原点Sまわり」で記述された足部とフォースプレート間に作用する力のモーメントを,「足部座標系fの原点まわり」に直接変換すると,
$$
\bm{M}(f) = \bm{M}(S) + {}^S_f \bm{p} \times \bm{F}
$$
のように書くことができる.これは座標系に依存しない表現であるが,座標系を明示的に示すと,
$$
\bm{M}(f)^0 = {}^0 \bm{R}_S ~\bm{M}^S(S) + {}^S_f \bm{p}^0 \times \bm{F}^0
$$
と書くことができ,全ての物理量を絶対座標系0に変換している.ここで右上付きの記号はどの座標系で計測しているかを明示し,$${{}^0 \bm{R}_S}$$はフォースプレート座標系Sから絶対座標系への座標変換行列である.
なお,フォースプレート座標系の軸方向はもちろんだが,原点もフォースプレート表面ではなく,埋め込まれたセンサの高さに位置することが多いので注意されたい.使用するフォースプレートの仕様をよく確かめていただければと思う.
もし,たとえば手先に外部環境(身体の外の世界.フォースプレートも外部環境)から力や力のモーメントが作用する場合などには,同様に平行軸の定理で,接触している部位の原点まわりの力のモーメントに変換して与えれば良い.
次章について
本章で述べた関節に作用するトルクを計算するコードは少し長くなるため,次章
で別途示すこととする.
上記の式は,並進の力の計算と同様に,再帰呼び出しによって計算を行う.
なお,これらの回転力の計算では,並進力$${\bm{f}}$$が媒介しているため,事前に(または逐次)それらを与えているが,多体系の合成の運動方程式を整理すれば,内力であるこの並進力を消去することができることは,繰り返し強調して述べた.この内力が見えない形式になると身体運動における関節に作用するトルクの物理的意味をより明確に示すことができ,次章で示す関節トルクを数値的に得るだけではなく,このことはバイオメカニクスにとってはるかに重要な意味を持つと考えている.関節に作用するトルクの物理的意味につていは別途述べることとする.
参考文献
1)コンピュータ制御機械システムシリーズ10,ロボット制御基礎論,吉川,コロナ社,1988
補足
補足1:懸命な読者は,「他の関節に作用する並進力がまだ消えていない」ことに気づくだろう.これはアルゴリズムの効率を優先するための式で,並進力も消える合成の運動方程式については別途述べる.



【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
