
動かして学ぶバイオメカニクス#4 〜床反力と関節に作用する力の計算〜
前章までに,身体の慣性パラメータと重心位置について述べた.ここでは,実際にニュートンの運動方程式を解くことで,身体に作用する力を計算しつつ,その物理的意味について考えていきたい.
多関節構造の運動方程式
これまで,ニュートンの運動方程式(Newton's equation of motion)を例題として取り上げたが,これは並進運動を記述する方程式である.
大きさを無視した質量だけを考慮する質点と異なり,物体には大きさや形があり,必然的に物体の運動には回転という概念が発生し,重心に関するニュートンの運動方程式ばかりでなく,物体の回転のダイナミクスも考える必要がある.この回転の力学を記述する運動方程式をオイラーの運動方程式(Euler's equation of motion)と呼ぶ.形のある物体の運動はニュートンとオイラーの運動方程式のこのセットで記述することができる.
座標系のとり方にも依存するが,同じ物体の運動を記述するにしても,ラグランジュの運動方程式(Lagrange's equation of motion)のように,運動方程式の「たて方(作り方,または導出)」には異なる方法がある.未来の運動を予測する運動方程式なのに,異なる表現方法が存在するのは不思議な気もするが,自由度が大きくなるほど記述の仕方にバリエーションが発生する.
一方,運動方程式の記述の仕方(たて方)だけでなく,同じニュートン・オイラーの運動方程式で解く際にも,異なる「解き方」が存在する.ひとつは,これまで述べてきたように,関節で結合している複数のリンクを解く際に,あるリンクの運動方程式を解いて,その子供の運動方程式を解くというように,漸化的に解く方法(ここでは漸化的運動方程式と呼ぶことにする)と,まとめて全部位(リンク)について解く方法とがある.後者を,ここではこれを合成の運動方程式と呼ぶことにする.特に回転の運動方程式は座標系のとり方によって,大きく運動方程式が異なる.
ここでは,このうちニュートンの運動方程式を解くことで,身体の各関節に作用する力を計算することを目的とする.
関節に作用する力の物理的意味
関節に作用する力は,怪我予防などに関連しリハビリや整形外科などの分野では比較的関心があるかもしれないが,スポーツバイオメカニクスでは,関節に作用するトルクの計算過程の媒介する変数や中間生成物ぐらいにしか捉えられていないかもしれない.恐らく運動のスキルと関節に作用する力が密接に関係すると考えている人が少ないからだろう.
しかしながら,ヒトが行う,投げる・跳ぶなどの一定の運動パターンを形成しているのは,関節に作用する力が重要な役割を果たしていることは,
で述べてきた.つまり,身体の末端にこの関節に作用する力が内力としてエネルギー伝達を媒介している.関節に作用するトルクはむしろこの伝達を促進する役割と考えている.
また,それらの力の和が,床反力に相当することは
で示してきたが,以下でも述べていく.
漸化的ニュートン・オイラー・アルゴリズム
ヒトやロボットのように多関節構造の逆動力学問題を解く方法として,ニュートン・オイラー法(Newton-Euler method)がある.もう少し詳しく述べると,これはLuh, Walker, Paulが開発した漸化的ニュートン・オイラー・アルゴリズム(Recursive Newton-Euler algorithm)(文献1),またはその派生のアルゴリズムを指す.
このアルゴリズムを,多少身体運動の問題にアレンジする必要があるが(身体の記述のほうが簡潔になる),バイオメカニクスでも一般的な方法である.これはオープンループ構造のロボットの計算方法で発展し,計算効率の良さが売りである.身体運動の逆動力学解析でも,一部の手順は異なるが,全身や多くの部分の関節に作用する力や力のモーメントを推定する際には,効率の良い方法である.
これに対して単純に合成した総和の運動方程式をたて,それを解く方法もある.これは,方法と呼ぶほど大げさではなく本質的な違いはないのだが,ニュートン・オイラー法に慣れ親しみすぎて,ニュートンとオイラーの運動方程式を部位ごとに逐次的にしか解けないと誤解をしている方が多いので別の章で示す.前述のように,この違いはニュートンの運動方程式では違いが少なく,オイラーの運動方程式で恩恵が得られるので,ここではこの程度に話をとどめておく..
なお,ここでは運動の物理的意味を考える上では重要なラグランジュの運動方程式については取り上げない予定であるが,多くのロボット工学の教科書で記述があるが,基礎を学びたい方は文献2,3などを参照されたい.
多関節構造のニュートンの運動方程式
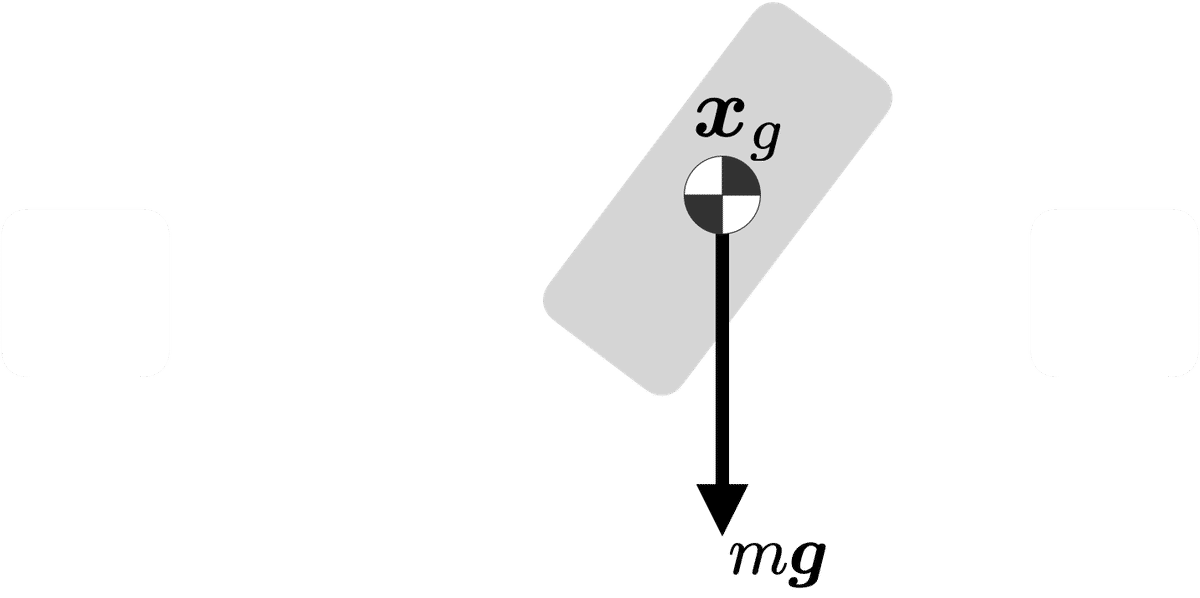
前章で取り上げたニュートンの運動方程式について復習する.図1に示す物体(剛体)の自由落下や放物運動などに相当するニュートンの運動方程式は
$$
m \ddot{\bm{x}}_{g} = m \bm{g}
$$
と書き表すことができる.ここで$${m}$$は物体の質量,$${\bm{x}_g}$$は物体の重心の位置ベクトル,$${\bm{g}}$$は重力加速度である.また,$${\ddot{\bm{x}}_g}$$は$${\bm{x}_g}$$に対する二階の時間微分で,物体の重心の加速度ベクトルに相当する.
ここで,物体の運動方程式は,重心$${\bm{x}_g}$$をこの物体の代表点として記述しているが,代表点として重心に重力が作用すると考えてよい理由は,前章
で述べたとおりである.
このように,他の物体との接触,すなわち相互作用がない場合は重力$${m\bm{g}}$$だけ作用する.しかし,他の部位との相互作用がある場合,さらに他の部位との相互作用力が発生する.
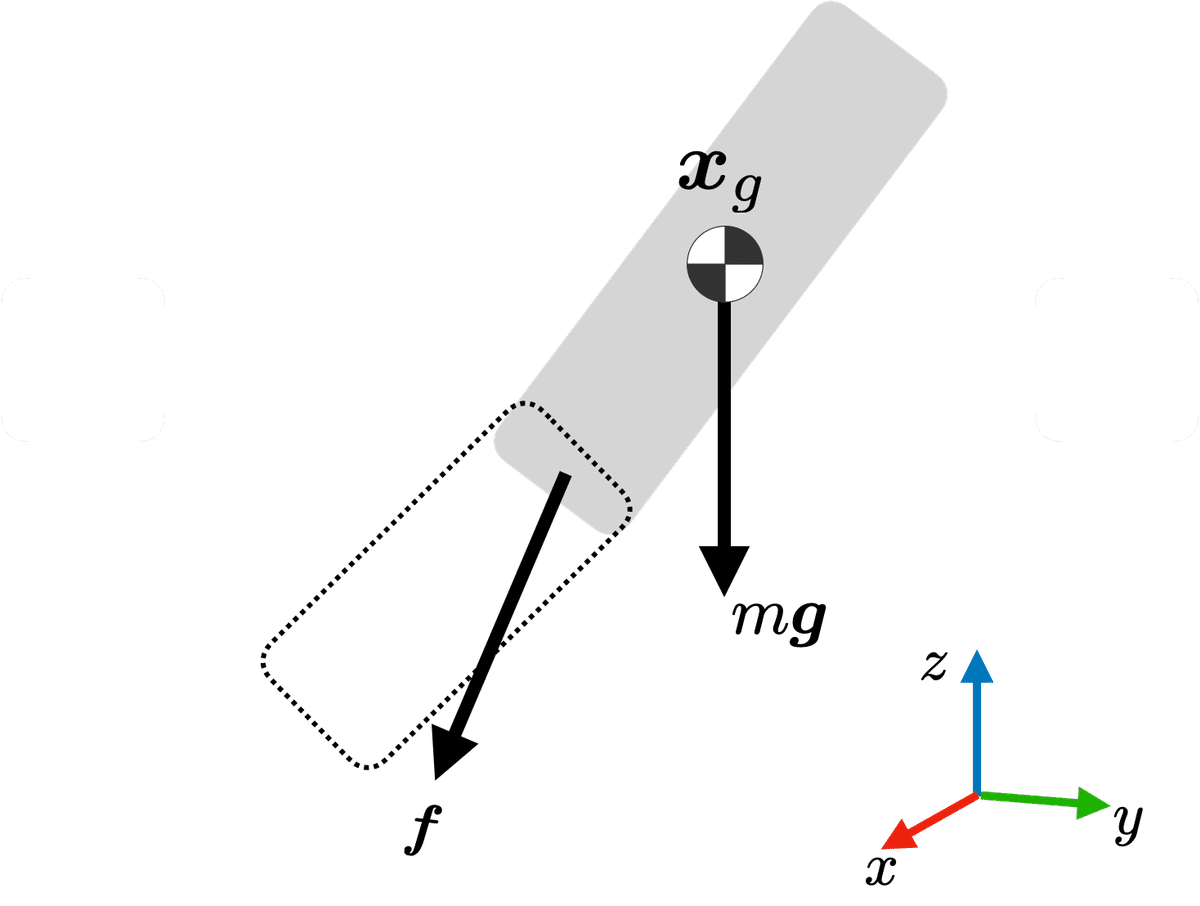
たとえば,図2のように隣の部位(リンク)が一つ増え,隣のリンクが自分のリンクに作用する力を$${\bm{f}}$$とすると(補足1),運動方程式は
$$
m \ddot{\bm{x}}_{g} = m \bm{g} + \bm{f}
$$
となる.これを成分で書くと
$$
m_i \begin{bmatrix}\ddot{x}_{g1} \\ \ddot{y}_{gi} \\ \ddot{z}_{gi} \end{bmatrix} = m \begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix} + \begin{bmatrix} f_x \\ f_y \\ f_z \end{bmatrix}
$$
となる.ここで,座標系を図2に示した$${xyz}$$(図中色をRGBで表現)とし,鉛直上方を$${z}$$軸とすると,重力加速度ベクトル$${\bm{g}}$$の$${z}$$成分は$${\bm{g}=[0~0~-g]^T}$$のように負の定数$${-g}$$となることに注意されたい(補足2).以降の計算では重力加速度$${g}$$は9.8とおいている.
多関節構造,すなわち多体系の運動方程式では,次に示すように複数の部位に対する記述が必要となる.
漸化的アルゴリズム
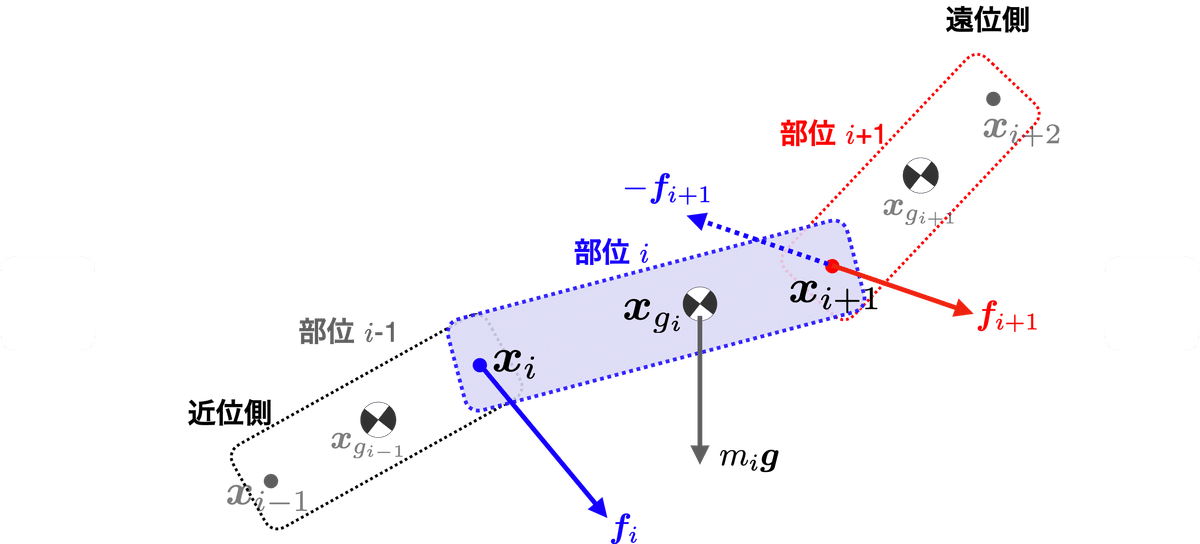
多体系の運動方程式のうち,図3に示すような親と子の部位(リンク)と接続し2つの関節を持つ部位ならば,各部位(リンク)の並進の運動方程式,すなわちニュートンの運動方程式は,
$$
m_i \ddot{\bm{x}}_{gi} = m_i \bm{g} + \bm{f}_i - \bm{f}_{i+1}
$$
となる.ここで,各部位の重心の位置ベクトルを$${\bm{x}_{gi}}$$とした.部位$${i}$$の近位側(根元側,親側)の関節には力$${\bm{f}_{i}}$$ が作用する.一方,遠位側(先端側,子側)の関節は子供に属する関節と定義するので,子供の部位$${i+1}$$の関節に作用する力$${\bm{f}_{i+1}}$$は部位$${i}$$に対しては反作用の力$${-\bm{f}_{i+1}}$$が作用することに注意をされたい.
もし末端の部位($${i=n}$$)が外部環境と接触せず,末端に相互作用の力が作用していない場合,末端の部位に作用する力は$${\bm{f}_{n+1}=\bm{0}}$$なので(ここで$${\bm{0}=[0~0~0]^T}$$は各成分が$${0}$$のゼロベクトル),
$$
m_n \ddot{\bm{x}}_{gn} = m_i \bm{g} + \bm{f}_n
$$
となり,末端の部位$${n}$$の重心$${\bm{x}_{gn}}$$の運動を計測し,パラメータ$${m_n}$$がわかれば,未知数は部位$${i}$$の関節に作用する力$${\bm{f}_n}$$だけとなる.
すると次の親側のリンクは
$$
m_{n-1} \ddot{\bm{x}}_{g~n-1} = m_{n-1} \bm{g} + \bm{f}_{n-1} - \bm{f}_{n}
$$
から,未知数$${\bm{f}_{n-1}}$$を解けば良い.
このように遠位側の部位から,逐次解く方法が漸化的なニュートンの運動方程式の解き方である.
合成の運動方程式
多関節構造のニュートンの運動方程式を漸化的に解くことは,結果的に合成の運動方程式を解くことと等価となり,部位全体に作用する外力を推定することになる.
このとき,部位間の関節に作用する力は作用反作用で打ち消し合うので,見かけ上計算には表れないが,漸化的計算では途中経過を保持しておけば,部位間の関節に作用する力も計算される.このことは,後半の再帰的呼び出しを用いたコードによって理解できるだろう.
前述のように,部位$${i}$$の運動方程式は
$$
m_i \ddot{\bm{x}}_{gi} = m_i \bm{g} + \bm{f}_i - \bm{f}_{i+1}
$$
となるが,2章
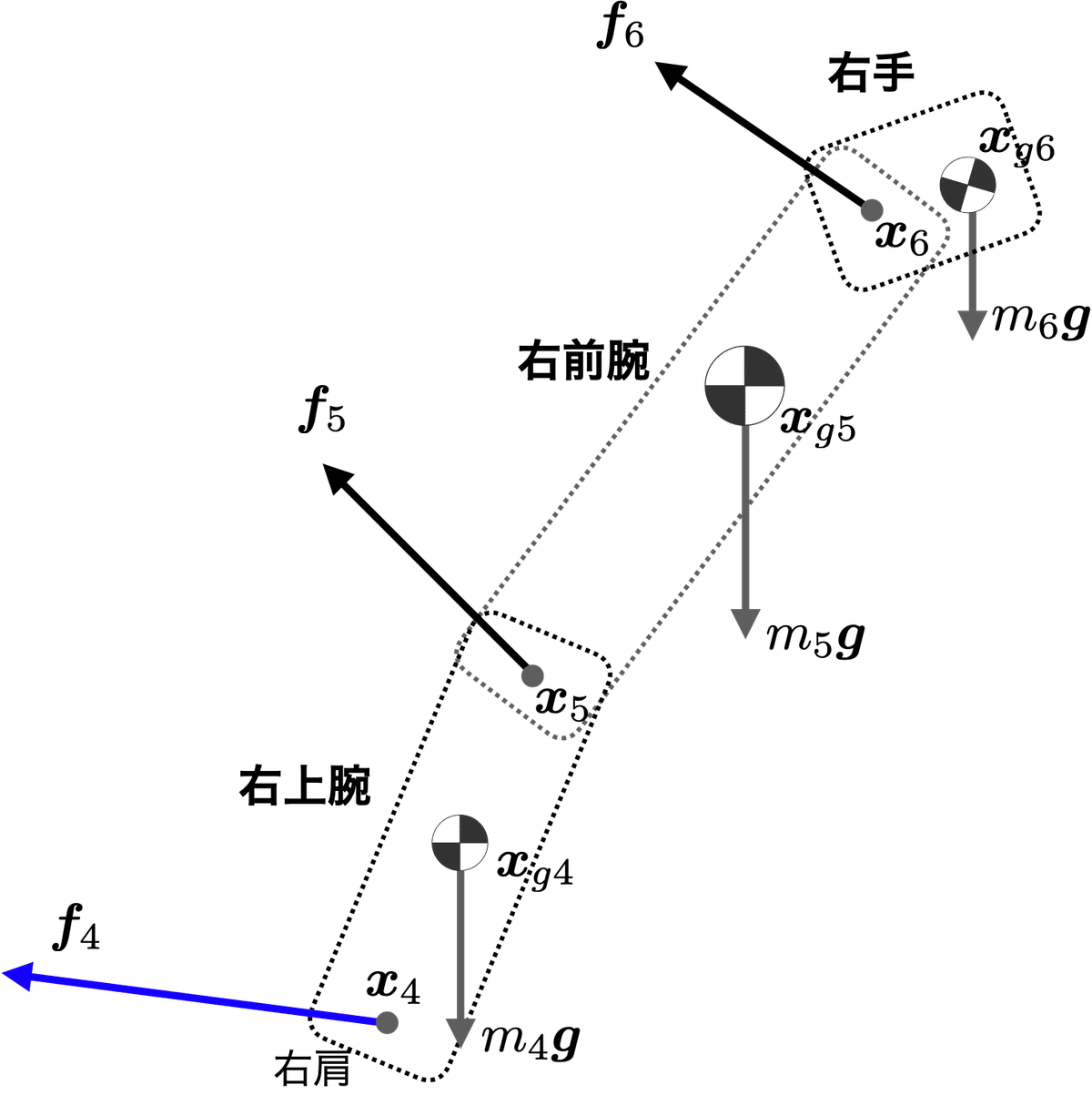
の図3などで示した,右上腕($${i=4}$$),右前腕($${i=5}$$),右手($${i=6}$$)から構成される右腕全体の運動方程式を全て加算すると,
$$
\sum_{i=4}^6 m_i \ddot{\bm{x}}_{gi} = \sum_{i=4}^6 \left(m_i \bm{g} + \bm{f}_i - \bm{f}_{i+1} \right) ~\\ = m_4 \bm{g} + m_5 \bm{g} + m_6 \bm{g} + \bm{f}_4 - \bm{f}_5 + \bm{f}_5 - \bm{f}_6 + \bm{f}_6\\ = \sum_{i=4}^6 m_i \bm{g} + \bm{f}_4 \\
\sum_{i=4}^6 m_i (\ddot{\bm{x}}_{gi} - \bm{g}) = \bm{f}_4 \\
m_{a} (\ddot{\bm{x}}_{ga} - \bm{g}) = \bm{f}_4
$$
を得る.ここで$${m_{a}=\sum_{i=4}^6 m_i}$$は右腕全体の質量,$${\bm{x}_{ga}}$$は右腕の合成の重心である.つまり右腕全体の運動方程式の外力は唯一,右肩関節$${\bm{x}_4}$$に作用する力$${\bm{f}_4}$$だけとなる.
このように系を右腕の$${i = 4〜6}$$と定めると,系内で作用する作用反作用の力(相互作用力)$${\bm{f}_5, \bm{f}_6}$$は打ち消し合って計全体の運動方程式から相殺される.また系内では$${\bm{f}_5, \bm{f}_6}$$が行う仕事も相殺されるため,このような系の外に対しては仕事を行わない力を内力(internal force)と呼ぶ.これに対して,右肩関節$${\bm{x}_4}$$に作用する力$${\bm{f}_4}$$は系の外から作用する力で,系全体に対して仕事を行う.これを外力(external force)と呼ぶ.
このように,関節に作用する同じ作用反作用の力でも,系の選択の仕方(見方)で外と内の境界が変わり,それにともない内力か外力かが定まることに注意をされたい.
全身の運動方程式
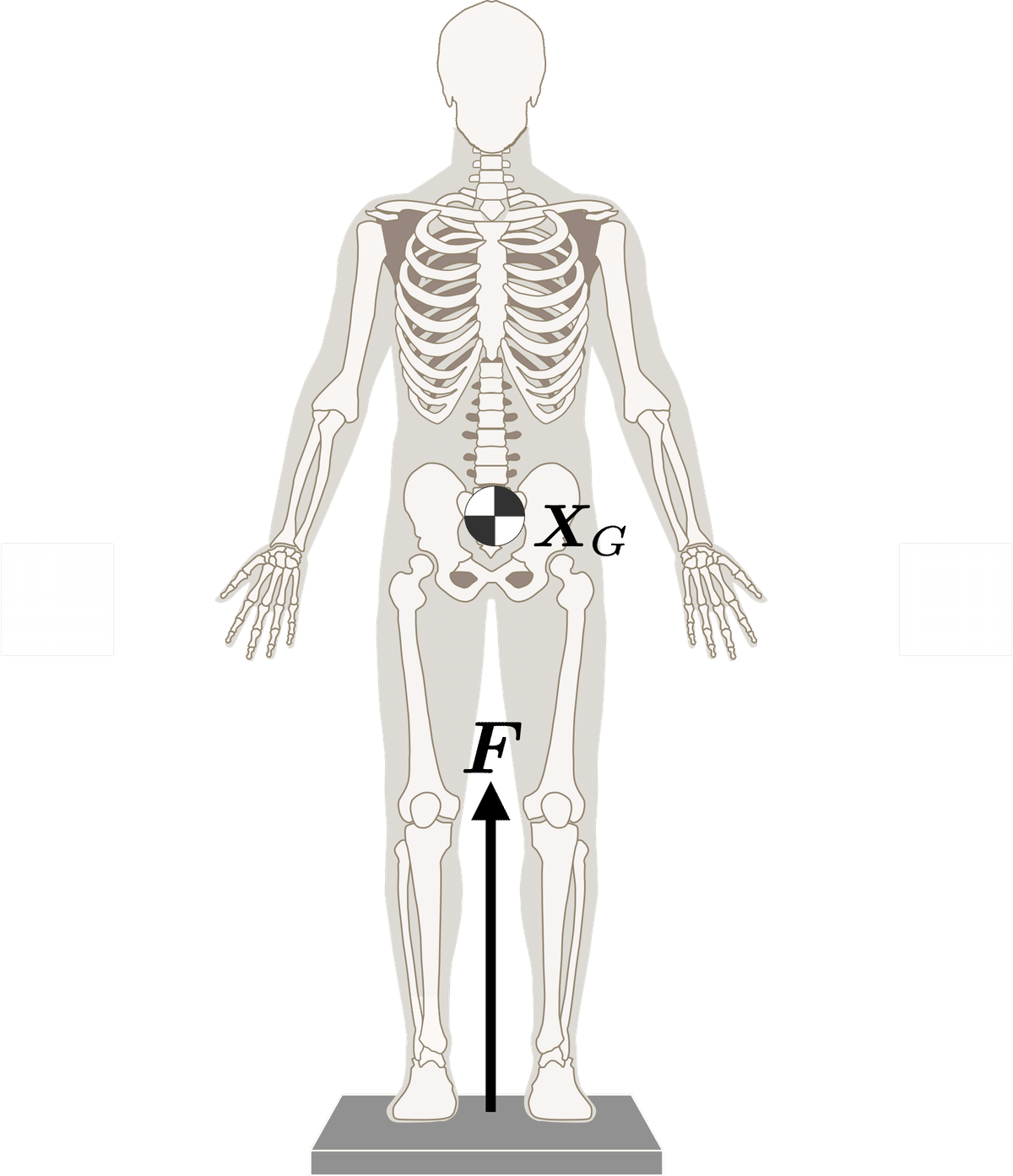
次に全身の運動方程式を考える.全身の部位を加算すると,全身の運動方程式は
$$
\sum_{i=1}^n m_i \ddot{\bm{x}}_{gi} = \sum_{i=1}^n \left(m_i \bm{g} + \bm{f}_i - \bm{f}_{i+1} \right) \\M \ddot{\bm{X}}_{G} = M \bm{g} + \bm{F} \\
M (\ddot{\bm{X}}_{G}-\bm{g}) = \bm{F}
$$
となる.最後の式は
$$
\sum_{i=1}^n \left\{m_{i} (\ddot{\bm{x}}_{gi} - \bm{g}) \right\} = \bm{f}_{n}
$$
と等価である.
ここで,身体は床とだけ接触し床から身体へ作用する力の総和を$${\bm{F}~(=\bm{f}_n)}$$とすると,これは床反力(ground reaction force)に相当する.また,$${\bm{X}_{G}}$$を全身の重心位置ベクトル,$${M=\sum_{i=1}^n m_i}$$を全身の質量とする.
この身体重心の加速度と床反力の関係については,フォースプレートと身体運動の関係について述べた
の記事も参照していただければと思う.
この身体全体の運動方程式は身体全体(全身)の重心に関する運動方程式となり,外力である床反力は重心の加速度と重力で定まる.
ただし,モーションキャプチャーとフォースプレートなどで身体重心の加速度と$${\ddot{\bm{X}}_{G}}$$と床反力$${\bm{F}}$$を計測することで比較できるが,運動中は必ずしも一致しない.若干の違いが発生する.特にジャンプなどの衝撃が加わると顕著となる.これは,身体側の筋肉や関節などに粘性抵抗があり,エネルギーの消散が全身で起こるからである.すなわち,この運動方程式のモデルには表れていない項も考慮することが重要であることを示唆している.
並進の運動方程式の解き方
ここでは,前述のニュートンの運動方程式を漸化式に書き換え,前章同様に再帰呼び出しと二分木探索を利用し,関節に作用する力を計算するコードを導く.
ただし,ニュートンの運動方程式を解く際には,加速度計算,すなわち二階微分の計算が必要となるが,加速度計算は次回のフィルタリングと合わせて詳しく述べる.そこで,今回はデータを前回と同様に,全身のモーションキャプチャーのデータと合わせて,加速度データをこのリンク先からファイル(sample_data_cg_acc_220918.csv)をダウンロードし計算に利用していただきたい.
なお,将来的にはコードの共有方法はGitHubなどに変更するかもしれないが,暫定的に以下の,Google Colaboratoryのリンクから,Pythonをインストールせずに,ブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,この計算をGoogle Colaboratoryで実行するには,
1.上記の加速度データをダウンロードし,
2.各自のGoogle Driveにデータをコピーし,
3.コード内のパスを各自の環境にあわせて設定する
必要があるので注意をされたい.
Google Colaboratoryについては,初期画面の解説や,ご自身で調べていただけると幸いである.
漸化的ニュートンの運動方程式による関節に作用する力の計算
関節に作用する力の計算も,これまで同様に漸化的に解くことができる.
漸化式(≒再帰呼び出し)は運動方程式
$$
m_i \ddot{\bm{x}}_{gi} = m_i \bm{g} + \bm{f}_i - \bm{f}_{i+1}
$$
から
$$
\bm{f}_i = m_i (\ddot{\bm{x}}_{gi} - \bm{g}) + \bm{f}_{i+1}
$$
と書くことができる.すなわち,再帰呼び出しとしては,上記の$${\bm{f}_i}$$がさらに
$$
\bm{f}_{i+1} = m_{i+1} (\ddot{\bm{x}}_{g~i+1} - \bm{g}) + \bm{f}_{i+2}
$$
を呼び出すように,再帰的に呼び出しを繰り返すことになり,並進の逆動力学計算は,
$$
\bm{f}_{n} = \sum_{i}^n \left\{m_{i} (\ddot{\bm{x}}_{gi} - \bm{g}) \right\}
$$
のように結果$${m_i (\ddot{\bm{x}}_{gi} - \bm{g})}$$を加算することを意味する.前節で導いた,全身の運動方程式と等しい.なお,再帰呼び出しについては第2,3章で復習をされたい.
まず,前回同様に,以下の計算で必要なPandasとNumpyのパッケージをimportする.ここでは,グラフを書くために,さらにmatplotlib.pyplotをインポートした.
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltダウンロードしたファイルのパスを,ご自身の計算環境にあわせて下記を参考に指定し,
file_path_4 = '/Users/…../sample_220908.csv' # Mac環境の例
file_path_4 = 'C:\Users\...\sample_220908.csv' # Windows環境の例下記の各リンクの重心の加速度データを抽出する関数を同様に定義する.前回は,マーカの位置ベクトルをデータから抽出したが(今回の計算では不要),今回は重心の加速度をニュートンの運動方程式を解く上で必要とし,異なるデータファイル(sample_data_cg_acc_220918.csv)に各リンクの重心加速度$${\ddot{\bm{x}}_{gi}}$$が収めたので,それを抽出する.
# CSVデータからヘッダだけ抽出
def extract_df_header(file_path):
return pd.read_csv(file_path, header=None, nrows=5, index_col=1).T
# skeletonの名前を抽出
def extract_skeleton_name(file_path):
df = extract_df_header(file_path)
marker_name = df['Name'][2]
position_col = marker_name.find(':')
return marker_name[:position_col]
# ファイル名とマーカの名前を引数に与えて各Linkの重心の加速度データを抽出する関数
def extract_cg_acc(file_path, marker_name):
sk_name = extract_skeleton_name(file_path) # skeleton
df_main = pd.read_csv(file_path, header=[4]) # データだけ抽出
df = extract_df_header(file_path) # headerだけ抽出
df_selected = df[df['Name']== sk_name+':'+marker_name] # ヘッダがName_Nameと一致する部分だけ抽出
selected_rows = df_selected.index # 一致する列
marker_data = np.array(df_main.iloc[:, selected_rows[-3:]].values) # 後ろから3個データを取得す
return marker_dataここまでは,前回とおおよそ同様である.
この関数を利用し,例えば
extract_cg_acc(file_path_4, 'RHand')のように関節名を指定すると,
array([[-9.139985, 0.592459, 7.176865],
[-8.999653, 0.374008, 7.060216],
[-8.858418, 0.160509, 6.948934],
...,
[-0.177999, -0.953488, 4.995204],
[-0.50509 , -1.296818, 5.047364],
[-0.843196, -1.643372, 5.095131]])のように部位RHandの重心の3次元の加速度データが得られる.このグラフを下記のコードで書くと,
acc_r_hand = extract_cg_acc(file_path_4, 'RHand')
plt.plot(np.arange(len(acc_r_hand))/360., acc_r_hand)
plt.xlabel('Time [s]')
plt.ylabel('Acceleration [m/s2]')
plt.legend(['x', 'y', 'z'])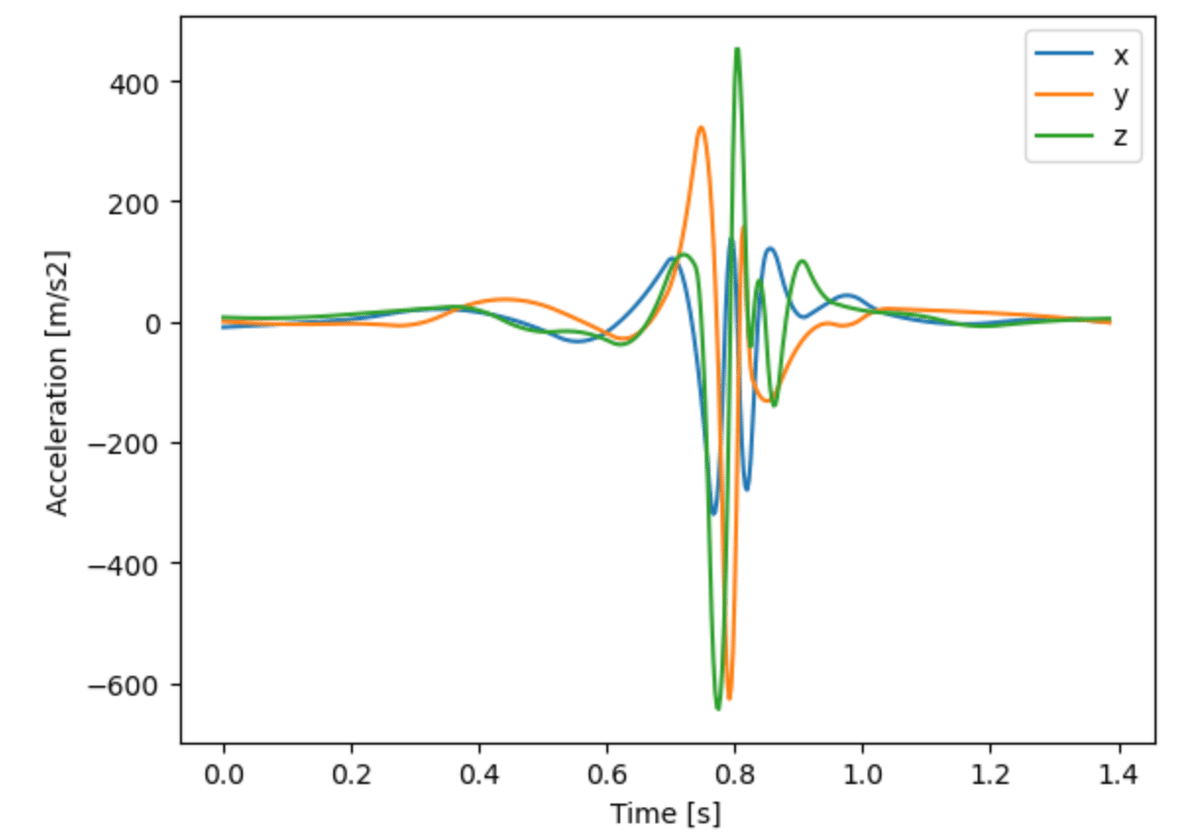
となる.
これで,逆動力学計算に必要な各リンクの重心の加速度ベクトルを抽出する準備が整った.前述のように,この加速度計算は次章で述べる.
ニュートンの運動方程式による漸化的な関節に作用する力の計算
以下のクラスは,前章で取り上げたclass BodyLinkに,各部位の重心の加速度をインスタンス変数に加えた class BodyLinkである.ただし,今回の計算に関しては重心位置の計算は不要なので,前章で使用したclass BodyLink_CGを必要としない.
また,前章のクラスをそのまま引き継ぎ,今回の計算に不要なインスタンス変数accを加筆しているので注意されたい.今後もこのclass BodyLinkに加筆していく作業を繰り返すことになる.
class BodyLink:
def __init__(self, l_id:int, name, mass_ratio:float):
self.l_id = l_id # linkのID
self.name = name # linkの名前
self.mass_ratio = mass_ratio # linkの質量分配比
self.child_val = None # 子供の変数
self.sister_val = None # 兄弟姉妹の変数
self.cg = None # linkの重心位置
self.acc = None # linkの重心の加速度
self.force = None # linkの関節に作用する力
# BodyLinkを一旦作成してから,その後に親子,兄弟姉妹関係をBodyLinkに与える.
def set_child_sister(self, child_val, sister_val):
self.child_val= child_val
self.sister_val = sister_val
# 合成の質量(全質量)の計算
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
# bw: 体重
def Resultant_Mass(self, bw, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return bw*self.mass_ratio + (self.child_val).Resultant_Mass(bw, sister)
elif sister == True: # 全身解析
return (bw*self.mass_ratio +(self.child_val).Resultant_Mass(bw, sister) +
(self.sister_val).Resultant_Mass(bw, sister))
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# m * cg
def WeightedJoint(self, body_weight):
return body_weight*self.mass_ratio * self.cg
# 合成の(全)WeightedJoint
# Σ m_i * cg_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_WeightedJoint(self, body_weight, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return self.WeightedJoint(body_weight) + \
(self.child_val).Resultant_WeightedJoint(body_weight, sister) #, sister)
elif sister == True: # 全身解析
return self.WeightedJoint(body_weight) + \
self.child_val.Resultant_WeightedJoint(body_weight, sister )+ \
self.sister_val.Resultant_WeightedJoint(body_weight, sister)
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 合成重心
# Resultant_WeightedJoint() / Resultant_Mass()
# = Σ(m_i * cg_i) / Σ m_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_Cg(self, body_weight, sister=False):
return self.Resultant_WeightedJoint(body_weight, sister)/self.Resultant_Mass(body_weight, sister)
# 各リンクの重心の加速度をBodyLinkの acc に与える
### 追加関数:次章以降では不要となる ###
def set_acc(self, file_path):
m_name = self.name # 指定したリンクの名前
return extract_cg_acc(file_path, m_name)
# m * (acc - g)
def CgForce(self, body_weight):
gravity = [0., 0., -9.8] # 重力加速度ベクトル
return body_weight*self.mass_ratio * (self.acc - gravity)
# Inverse Dynamics Newton equation
def ID_Newton(self, body_weight, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
f = self.CgForce(body_weight) + \
self.child_val.ID_Newton(body_weight, sister)
self.force = f
return f
elif sister == True: # 全身解析
f = self.CgForce(body_weight) + \
self.child_val.ID_Newton(body_weight, sister) + \
self.sister_val.ID_Newton(body_weight, sister)
self.force = f
return f
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
b_link = [0] * 16 #配列の初期化
b_link[0]=BodyLink(0, '', .0) # 0のときストップ
b_link[1]=BodyLink(1, 'Hip', .187)
b_link[2]=BodyLink(2, 'Chest', .302)
b_link[3]=BodyLink(3, 'Head', .069)
b_link[4]=BodyLink(4, 'RUArm', .027)
b_link[5]=BodyLink(5, 'RFArm', .016)
b_link[6]=BodyLink(6, 'RHand', .006)
b_link[7]=BodyLink(7, 'LUArm', .027)
b_link[8]=BodyLink(8, 'LFArm', .016)
b_link[9]=BodyLink(9, 'LHand', .006)
b_link[10]=BodyLink(10, 'RThigh', .110)
b_link[11]=BodyLink(11, 'RShin', .051)
b_link[12]=BodyLink(12, 'RFoot', .011)
b_link[13]=BodyLink(13, 'LThigh', .110)
b_link[14]=BodyLink(14, 'LShin', .051)
b_link[15]=BodyLink(15, 'LFoot', .011)
# 親子関係と兄弟姉妹関係を下記でb_linkのchild_val, sister_valに追記
child_sister_list = [
[1,2,0], [2,3,10], [3,0,4], [4,5,7], [5,6,0], [6,0,0], [7,8,0],
[8,9,0], [9,0,0], [10,11,13], [11,12,0], [12,0,0], [13,14,0],
[14,15,0], [15,0,0]]
[b_link[i[0]].set_child_sister(b_link[i[1]], b_link[i[2]]) for i in child_sister_list];上記コードの最後の部分(「# 親子関係と兄弟姉妹関係を下記でb_linkのchild_val, sister_valに追記」以下)は,前章で
# 親子関係と兄弟姉妹関係を下記でb_linkのchild_val, sister_valに追記
b_link[1].set_child_sister(b_link[2], b_link[0])
b_link[2].set_child_sister(b_link[3], b_link[10])
b_link[3].set_child_sister(b_link[0], b_link[4])
b_link[4].set_child_sister(b_link[5], b_link[7])
b_link[5].set_child_sister(b_link[6], b_link[0])
b_link[6].set_child_sister(b_link[0], b_link[0])
b_link[7].set_child_sister(b_link[8], b_link[0])
b_link[8].set_child_sister(b_link[9], b_link[0])
b_link[9].set_child_sister(b_link[0], b_link[0])
b_link[10].set_child_sister(b_link[11], b_link[13])
b_link[11].set_child_sister(b_link[12], b_link[0])
b_link[12].set_child_sister(b_link[0], b_link[0])
b_link[13].set_child_sister(b_link[14], b_link[0])
b_link[14].set_child_sister(b_link[15], b_link[0])
b_link[15].set_child_sister(b_link[0], b_link[0])としていた部分を置き換えている.
重心の加速度ベクトルの代入
新たに加えたインスタンス変数accに,ニュートンの運動方程式の逆動力学計算の核となる重心の加速度ベクトルを代入する.
本章で追加した関数set_acc()は,先程定義したextract_cg_acc()を利用し,各リンクの重心の加速度ベクトルをインスタンス変数accに代入するメソッド(関数)である.
これを利用し,逆動力学計算の前にインスタンス変数accに重心の加速度ベクトルを代入するが,例えば以下のように
b_link[4].acc = b_link[4].set_acc(file_path_4)リンク4,すなわち右上腕(RUArm:4)に重心の加速度ベクトル$${\ddot{\bm{x}}_{g4}}$$を,インスタンス変数accに与えている.
これを,全リンクに対して行うには,下記のように
for i in range(1,16):
b_link[i].acc = b_link[i].set_acc(file_path_4)繰り返せばよい.
逆動力学計算
これまでの議論からも,ニュートンの運動方程式の逆動力学計算は,結果,
$$
m_i (\ddot{\bm{x}}_{gi} - \bm{g}) =m_i \left(\begin{bmatrix}\ddot{x}_{g1} \\ \ddot{y}_{gi} \\ \ddot{z}_{gi} \end{bmatrix} - \begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix}\right)
$$
の加算
$$
\sum m_i (\ddot{\bm{x}}_{gi} - \bm{g}) = \sum m_i \left(\begin{bmatrix}\ddot{x}_{g1} \\ \ddot{y}_{gi} \\ \ddot{z}_{gi} \end{bmatrix} - \begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix}\right)
$$
を意味する.
関数ID_Newton()は,本章の目的である,各リンクの関節に作用する力を計算するclass BodyLinkのメソッド(関数)であり,ニュートンの運動方程式の逆動力学計算によって各関節に作用する力$${\bm{f}_i}$$を計算する.
この関数の中の再帰計算の途中の
self.force = fの部分では,各リンクに作用する力を代入している.
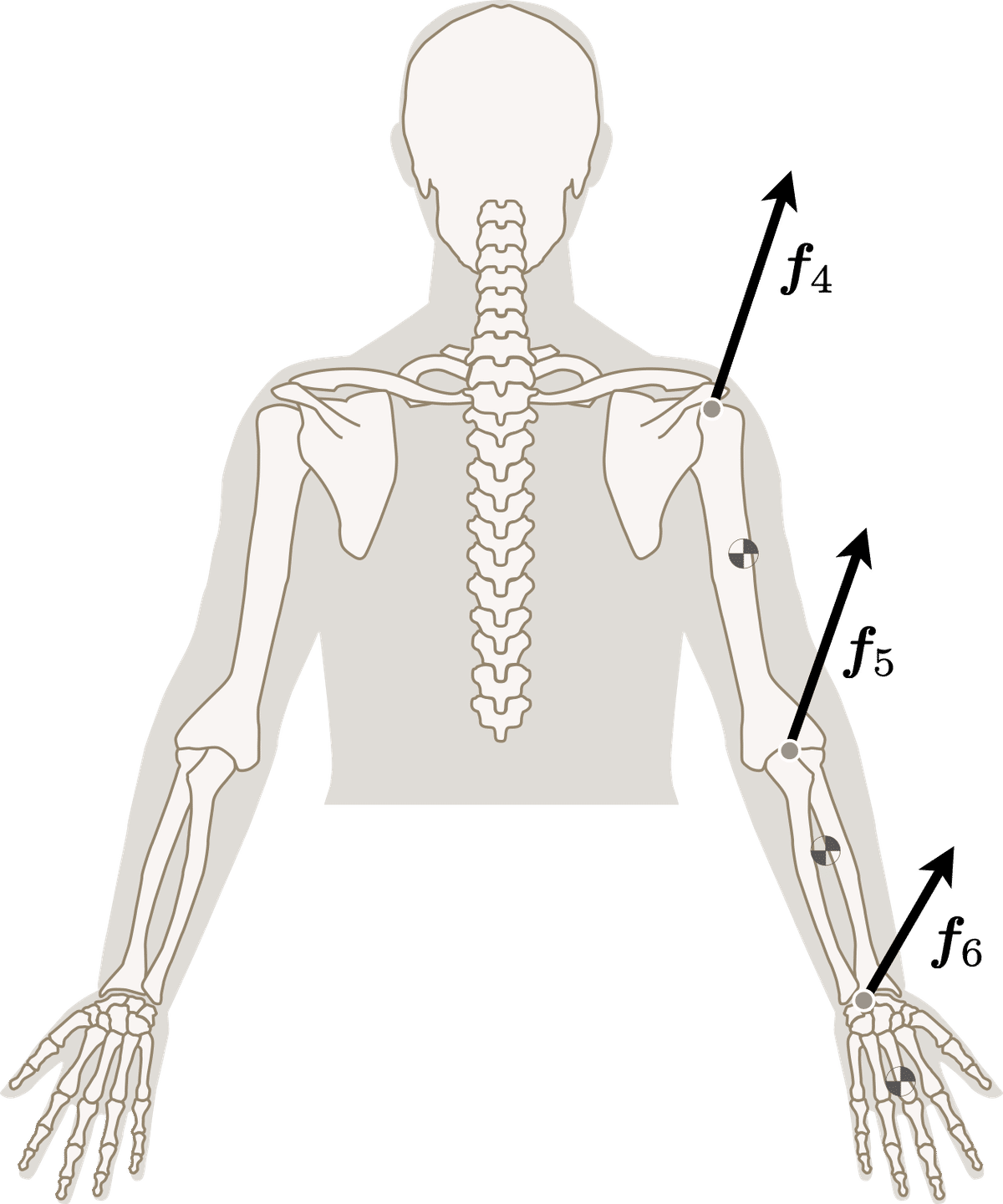
例えば,体重を86.0 [kg]と設定し,
b_link[4].ID_Newton(86.) # sister = False (default)を計算すると(オプションのsister =0として,兄弟姉妹のリンクを計算していないことに注意),リンク4,すなわち,右上腕(l_id = 4)の関節である右肩関節に作用する力 b_link[4].force ,すなわち
$$
\bm{f}_{4} = \sum_{i=4}^6 \left\{m_{i} (\ddot{\bm{x}}_{gi} - \bm{g}) \right\}
$$
を
### [出力]
array([[-28.26637732, -14.85425153, 31.20391079],
[-27.80596531, -14.39475654, 32.02744585],
[-27.34510034, -13.94148477, 32.84345418],
...,
[ 14.1557493 , -14.06374951, 54.01247105],
[ 13.90528358, -15.00390452, 54.32881913],
[ 13.64335528, -15.95454602, 54.64738171]])のように返すが,それ以外に,再帰呼び出しの途中で,右前腕(l_id = 5)の右肘関節に作用する力 b_link[5].force ($${\bm{f}_5}$$),右手(l_id = 6)の右手首関節に作用する力 b_link[6].force ($${\bm{f}_6}$$)も計算してくれる.
b_link[5].force
### [出力]
array([[-16.39675914, -11.04122335, 17.13344064],
[-16.15382565, -10.72380922, 17.45241206],
[-15.9096474 , -10.41191009, 17.77016796],
...,
[ 3.43597159, -8.99036294, 22.35627586],
[ 3.03556505, -9.68545175, 22.31413035],
[ 2.6209931 , -10.38809205, 22.26627668]])
b_link[6].force
### [出力]
array([[-4.71623226, 0.30570884, 8.76006234],
[-4.64382095, 0.19298813, 8.69987146],
[-4.57094369, 0.08282264, 8.64244994],
...,
[-0.09184748, -0.49199981, 7.63432526],
[-0.26062644, -0.66915809, 7.66123982],
[-0.43508914, -0.84797995, 7.6858876 ]])つまり,b_link[4].ID_Newton(86., sister=0) $${\bm{f}_4}$$を計算すれば,その先の子供のリンクの関節に作用する力全て$${\bm{f}_5, \bm{f}_6}$$を計算するため,b_link[5].ID_Newton(86., sister=0),b_link[5].ID_Newton(86., sister=0)を計算する必要がない.
全身の関節に作用する力と床反力の計算
b_link[1](Hip)は二分木で表したリンク機構の一番上の親(頂点)に相当する.そのHipに対してニュートンの運動方程式の力学計算を下記のように
b_link[1].ID_Newton(86., True)行うことで,b_link[1].forceすなわち,関節に作用する力の総和,すなわち床反力に相当する力を
### [出力]
array([[ 14.63653617, 140.3638164 , 861.57429209],
[ 14.50606651, 140.55716986, 863.64672259],
[ 14.37837431, 140.75301138, 865.6958826 ],
...,
[136.06508155, -28.1169008 , 662.97862112],
[136.96741178, -26.87789209, 657.02895459],
[137.86060958, -25.62677175, 651.02373498]])のように出力し,再帰呼び出しの計算過程で,全身の関節に作用する全ての力(b_link[1].force〜b_link[15].force)も計算し,インスタンス変数に格納される.ここで,オプションのsister =1として,兄弟姉妹のリンクを計算していることに注意されたい.つまり全身の計算を行い,床反力を
$$
\bm{F} = \sum_{i=1}^n m_i (\ddot{\bm{x}}_{gi} - \bm{g}) = \sum_{i=1}^n m_i \left(\begin{bmatrix}\ddot{x}_{g1} \\ \ddot{y}_{gi} \\ \ddot{z}_{gi} \end{bmatrix} - \begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix}\right)
$$
の計算を通して推定していることになる.
以下に,その床反力相当の力をグラフに出力した.
1行目の grf = b_link[1].force は,先程の計算結果を利用している.
再度計算するなら,grf = b_link[1].ID_Newton(86., sister=1) としてもよい.
grf = b_link[1].force
# grf = b_link[1].ID_Newton(86., sister=1) と同じ
plt.plot(np.arange(len(grf))/360.,grf)
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])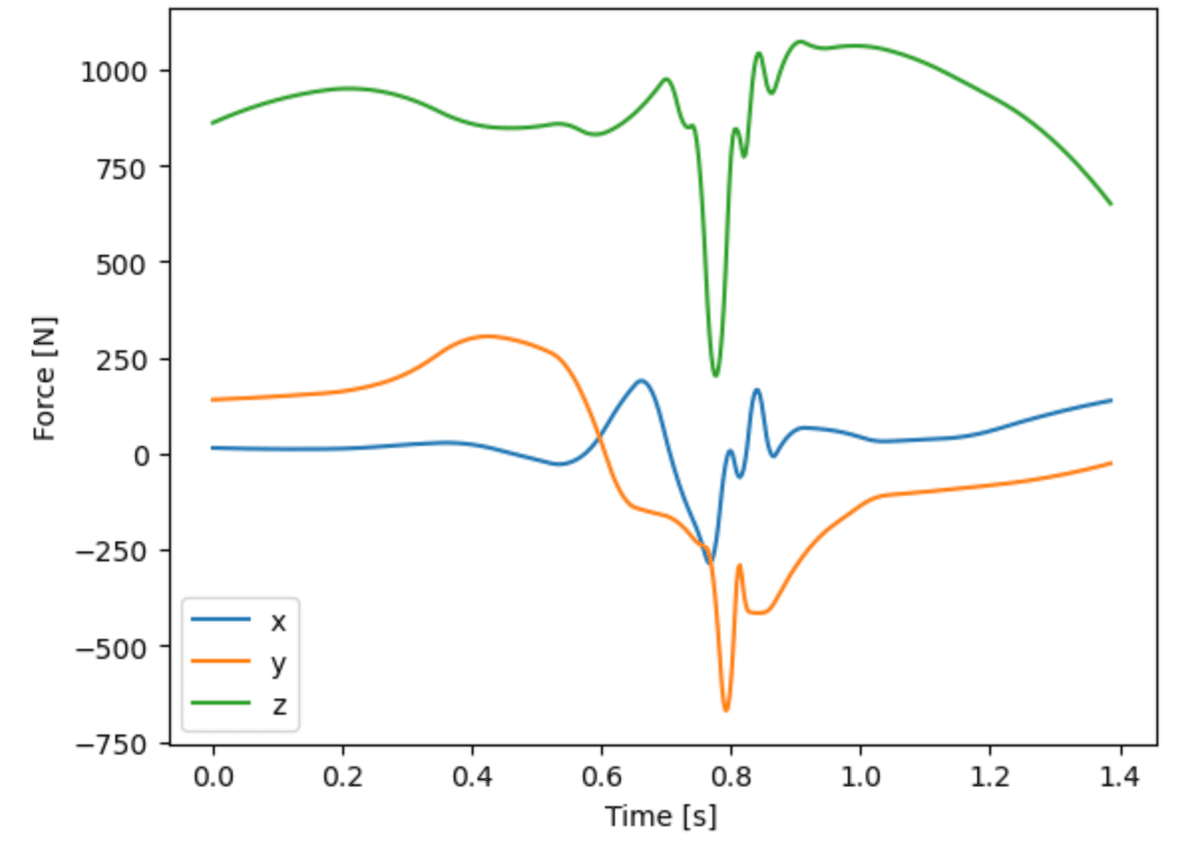
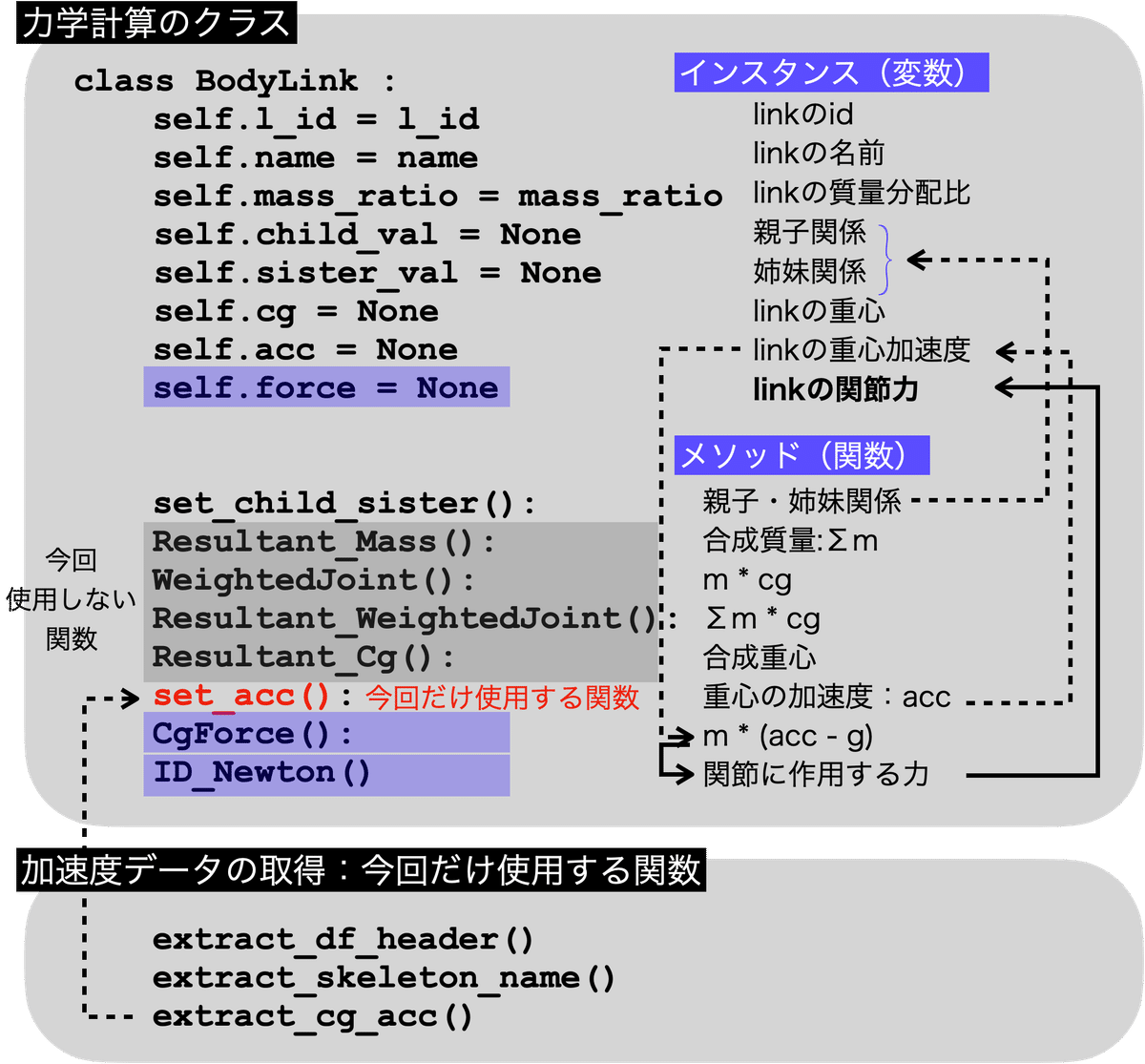
今回作成したクラスと関数の構造について,図9にまとめた.
まとめ
多体系のニュートンの運動方程式のとどのつまりは
$$
\sum m_i (\ddot{\bm{x}}_{gi} - \bm{g})
$$
である.これはモーションセンサが
$$
m (\ddot{\bm{x}}_{g} - \bm{g})
$$
を計測していることと似ていて面白い.つまりモーションセンサは加速度を計測しているというよりは,むしろ力学計算に適していることを示している.
ここで示したコードは,力学計算の本質と二分木探索(再帰呼出し)を利用することで,効率よく,また見通しよく,全身,または部分的な部位の関節に作用する力を導出している.
リンクの構造を表す二分木,すなわちclass BodyLinkの構造だけ,面倒だが丁寧に記述しておけば,あとは上記の短い CgForce()とID_Newton() のコードを記述するだけで,全身の計算を行ってくれる.
2次元回転から3次元回転の記述がかなり複雑化するように,回転運動の記述は並進運動と比較し煩雑になる.そこでオイラーの運動方程式を記述するコードを簡潔にし間違いをなくすためにも,この準備は意味を持つ.
次章について
ここでは,逆動力学計算の重要部分の加速度計算をこちらで行い結果をファイルで提供したが,次章
でその計算方法について述べる.この計算方法が逆動力学計算の精度を決定づけるので,精度の観点では最も重要といえる.
補足
補足1:力の作用
力は,何が何に対して作用するか明確に定義する必要がある.AがBに作用する力を$${\bm{f}_{\vec{AB}}}$$とすると,BがAに作用する力は,$${\bm{f}_{\vec{BA}} = -\bm{f}_{\vec{AB}}}$$のように$${\bm{f}_{\vec{AB}}}$$の反作用の力となる.定義が何に対して作用する力か定義を明確にすることを心がけることが大切である.
補足2:ベクトルと行列の転置
ここで,行列やベクトルの記法について確認する.
たとえば2次の行列
$$
\bm{A} =\begin{bmatrix} a & b \\ c & d \end{bmatrix}
$$
の転置(transpose)は
$$
\bm{A}^T =\begin{bmatrix} a & c \\ b & d \end{bmatrix}
$$
のように対角要素$${b, c}$$を入れ替えた行列となる.ここでは,記号として右肩に$${^T}$$を添えている.
この行列の記法に従い,縦ベクトル
$$
\bm{x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix}
$$
の転置は
$$
\bm{x}^T = \begin{bmatrix} x & y & z \end{bmatrix}
$$
と横ベクトルで書くことができる.このことを利用し,文章中のスペースの関係で$${\bm{x} = [x~y~z]^T}$$と記述することを多用することに留意されたい.
また,このことを利用し,ベクトル$${\bm{u} = [u_x~u_y~u_z]^T}$$とベクトル$${\bm{v} = [v_x~v_y~v_z]^T}$$の内積は,例えば
$$
\bm{u} \cdot \bm{v} = u_x v_x + u_y v_y + u_z v_z
$$
のように記述される事が多いが,ここでは
$$
\bm{u}^T \bm{v} = \begin{bmatrix} v_x & v_y & v_z \end{bmatrix} \begin{bmatrix} u_x \\ u_y \\ u_z \end{bmatrix} = u_x v_x + u_y v_y + u_z v_z
$$
のように記述する.
参考文献
1)J. Luh, M. Walker, R. Paul, On-Line Computational Scheme for Mechanical Manipulators, Journal of Dynamic Systems Measurement and Control-transactions of The Asme, Vol.102, 1980, pp.69--76
2)有本,関本,ロボット・メカトロニクス教科書・力学入門,オーム社,2011
3)前野,よくわかる解析力学,東京図書,2013


【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
