
身体における運動パターン形成 #3 〜ハンマー投〜
ハンマー投の加速方法
はじめに
ここでは,ハンマー投のスイング運動を例に取り上げ,その加速方法について述べていく.
で,内力が関節をまたいだエネルギー伝達を媒介し,この伝達がスイング運動のパターン形成に寄与することを述べた.
そこでここでハンマーと腕から構成される二重振り子の系を考えると,このシステムは劣駆動系となり,内力,すなわちハンマーのワイヤーに作用する張力を介したエネルギー伝達だけで,ハンマーを加速することになる.ハンドルと腕間にはアクチュエータは存在しないため,この内力によるエネルギー伝達がハンマー投の基本的な運動パターンを形成することを示していく.
ハンマー投のスイング運動
そもそも,このタイトルに違和感を感じる方もいるかもしれない.ハンマー投競技の投擲運動では3〜4回転ほどの回転運動をおこなっているが,その前の予備動作を除けば,ハンマー投の運動ではぐるぐるまわっているだけで,スイング運動をおこなっているようには見えないだろう.高速の回転運動で見た目にはわかりにくいということもあるが,実際にモーションキャプチャでハンマーと腕の運動を精密に計測し,左右の腕を一つの振り子とみなしハンマーと合わせて二重振り子と捉えると,腕とハンマーは全体的に回転運動を行いつつも,ハンマーと腕の間に相対的にわずか10~20degほどの振幅だが,腕とハンマーは二重振り子のような振動運動,すなわちスイング運動を繰り返している.
ハンマー投競技の特徴
陸上競技のハンマー投がどのような競技かご存じの方も多いと思うが,物理的なメカニズムを理解する上で必要なルールや競技の特徴をあらかじめ述べておく.

競技で使用するハンマーは,男子で7.26kg,女子で4.0kgのハンマーヘッドと呼ばれる金属球部分,長さが約1mのワイヤー,そして幅が約100mmのハンドルから構成される.ハンドルとワイヤーが小さなリング状の部分で接続され,この部分がハンマーと腕の関節に相当する.この関節には筋肉やモータなどのアクチュエータは介在しないので,腕を含めた二重振り子として考えると関節(リング部分)には内力だけが作用し,これは前章で述べた劣駆動系に相当する.
このハンマーをサークルと呼ばれる直径2.135mの円内から投擲するが,予備動作の後に,通常,全身で3,4回転してから投擲する.最大でも4回ほどの回転数となる理由は,そのぐらいの回転数でハンマーヘッドの速度は上限に達し,それ以上回転しても速度は上がらないためである.なお,サークル内では同じ場所にとどまって回転を行うのではなく,サークル内の投擲方向に対して反対方向から,少しづつ投擲方向に移動しながら回転を行っている.ハンマーと腕を二重振り子とみなすと,それらはほぼ一定の傾いた面内で回転運動を繰り返すが,その傾斜角は回転中に次第に大きくなる傾向にある.

図2に示すように,回転中,両足を接地している両足期と,片足だけで身体を支えている片足期があり,両足期にハンマーのエネルギーを増加させ,片足期にはハンマーから腕にエネルギーが戻ってきてしまい減速する.ただし平均的には増加するエネルギーが多いため,加減速を繰り返しながらハンマーは平均的に加速していく.また,高速に回転しているが,身体に固定された回転する座標系から見ると,わずか10~20度ほどの小さい相対角度ではあるが,腕とハンマーは二重振り子の基準振動のように振動をしている.
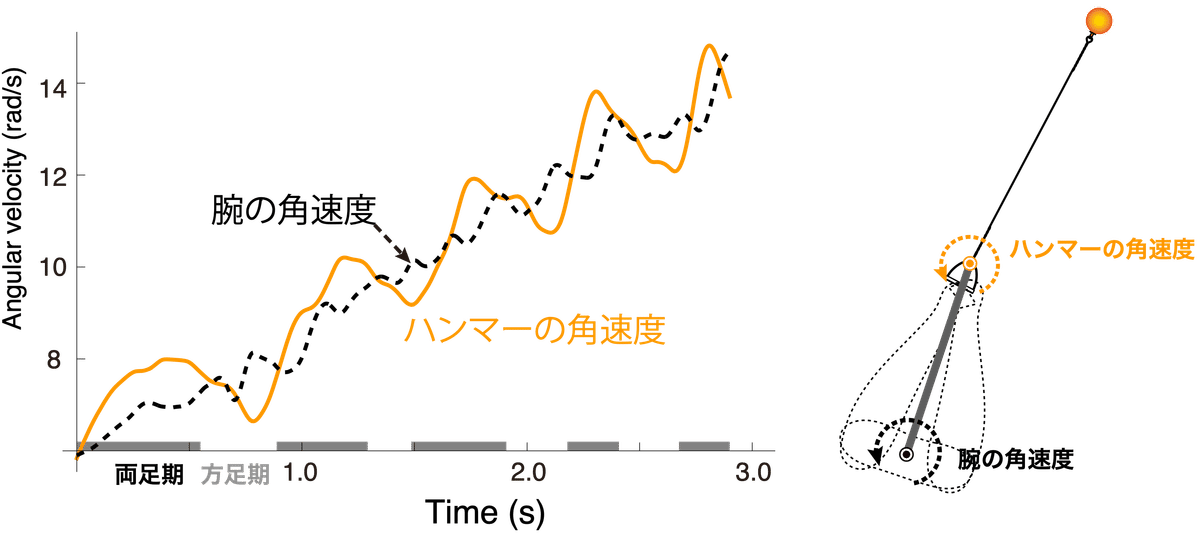
相対角度ではないが,図3はハンマーと腕の角速度(回転速度)のグラフで,ハンマーが腕に対して先行したり遅れたりしながら回転をしていることを示している.また,ハンマーの角速度が上昇し始めるのが両足期の開始とおおよそ一致し,片足期に入るとハンマーが腕よりも遅れ始めることも示している.
また,サークルを時計に見立てて投擲方向を時計の12時方向とすると(図2参照),両足期は反時計回りに回転する選手ではおおよそ10時から4時ぐらいの間に位置する.そして両足期の6時近辺のハンマーの位置がローポイントと呼ばれ,先程述べた傾斜面の中でハンマーヘッドが最も下に位置し,各回転でハンマーが最も加速する位置に相当する.一方,片足期の12時付近がハイポイントと呼ばれている.
高速ターンをしているため,動画を見ても振動になっていることはなかなかわかりづらいが,ハンマー投も一種のスイング運動を繰り替えしていると考えてよい.ハンマー投の投擲の様子は,たとえば下記動画(第96回日本陸上競技選手権大会 ハンマー投決勝,日本陸上競技連盟より)などをご参照いただきたい.
ハンマー投がこのような加速方法を採用するのは,ハンマーの質量と慣性モーメントが非常に大きいことに起因し,ぐるぐる回転はしているが,常にハンマーと身体間での綱引き状態にあり,大きな力に拮抗して投擲するためには,このような加速方法を採用するしかない.しかし,女子用ハンマーの質量が男子用と比較して半分近くであることを考えると,将来,身体能力の向上にともない相対的なハンマーの重さが軽くなり,投擲方法の変革が女子のハンマー投競技から起こる可能性もあるのではないだろうか.
また,世界記録レベルの80m以上の投擲を行う際には,身体には一瞬ではあるが両足期に最大約3000N,すなわち約300 キログラム重以上の力がハンマーを通じて身体全体に作用する.いわば,300 キログラム重の力で引っ張るハンマーと綱引き状態,または300kgのバーベルでデッドリフトをしている状態に近い.
ハンマーの加速の基本1:パラメータ励振
高速な回転運動中,身体にはハンマーの遠心力が作用し,その遠心力に負けないように身体を傾ける.この状態を身体に固定された回転している座標系から見ると,すなわち選手目線で眺めると,ハンマーと身体間で力の釣り合いがバランスし,ハンマーとの綱引き状態になっている(図4参照).

そしてこのとき,パラメータ励振と呼ばれる,回転角度に合わせた周期的な牽引動作による加速方法が取られる.このハンマー投の加速方法は,同様にパラメータ励振を用いて加速している「ブランコの加速方法」と似た加速方法が採用されている.そこで,ハンマー投の加速方法を述べる前に,ブランコの加速方法について説明する.
ブランコの加速方法

ブランコの場合,スイング中,加速するために屈伸したり反対に伸び上がる運動を繰り返す.このとき重りの位置が身体重心に相当し,ワイヤー方向に伸縮する振り子と考えて良く,このような振り子は糸やワイヤーの長さが変化する可変長振子とみなすことができる(図5参照).そしてブランコのスイング運動中,重心位置はおおよそ八の字運動を行う.ただし,図5のモデルでは瞬間的に振り子の長さが変わる,すなわち瞬間的に膝の伸展屈曲をしていると,説明の都合上仮定している.
また,振り子(ワイヤ)に作用する力は張力と呼ばれ,張力には向心力(遠心力の反作用の力(図3の$${F}$$)と重力$${m \bm{g}}$$が作用し,張力にはワイヤー軸方向成分だけ作用する.ここで,向心力は最下点の$${F_l}$$と最高点の$${F_h}$$と区別している.
ここで,前章
の力学的エネルギー変化の原理を思い出してほしい.前章では,物体に力ベクトルが作用し運動する時,「運動(速度ベクトル)の方向」と「作用する力(張力)の方向」が近いほうがエネルギーがより増加することと,その単位時間あたりのエネルギー変化はその力ベクトルと速度ベクトルの内積で決まることを述べた.
ブランコの場合,重り(人)に作用する重力と,ブランコの振動によって発生する力がもっとも大きくなるのが最下点の$${F_l}$$であるが,そのときにさらに,ブランコの回転軸方向に$${\Delta l}$$だけ伸び上がることで(赤色の矢印の速度ベクトルに相当),「上側」に速度が発生し,ブランコの力学的エネルギーが$${F_l \Delta l}$$だけ増大する.
一方,ブランコが最も高く上がったときの張力$${F_h}$$は,重力のワイヤ軸方向成分も弱まり,かつ回転運動も止まって向心力が作用せず,ブランコに作用する張力が最も小さくなる.この最上位の位置で,下側に$${\Delta l}$$だけしゃがみ込むことで速度ベクトルが下向きになり(青色の矢印),結果,力と速度の向きが反対となり振り子のエネルギーが$${F_h \Delta l}$$分減少してしまう
ただし,身体の屈伸と伸展の変化量$${\Delta l}$$が同じだとすると,最下点で膝を屈伸することによるエネルギー増大と,最上点で膝を伸展することによるエネルギー減少を差し引くと,$${(F_l - F_h)>0}$$なので,半周期の間に振り子に作用する力の差$${(F_l - F_h)\Delta l}$$だけエネルギーが増加し,平均的にはブランコのエネルギーは増加していく.
ハンマー投のパラメータ励振
以上がブランコのパラメータ励振による加速であったが,ハンマー投の加速方法も同様な原理で回転を加速する.ハンマー投では振動ではなく全体的には回転運動を繰り返し,重力と向心力によって張力が最大になるローポイントで引っ張りエネルギーを増加させ,反対側の張力が小さくなるハイポイントでは片足で支えているためハンマーに逆に引っ張られてしまいエネルギーが減少する.しかしブランコと同様に,増加分が減少分よりも上回るため,回転ごとにハンマーの速度が増大していく(図3参照).
このことから,ハンマーでは回転しつつ全体的には投擲方向に身体が移動していくことになる(図6右).
図6左は,ブランコのパラメータ励振と同様に,あくまでもハンマーの加速方法の原理をパラメータ励振によって説明するための図である.二重振り子の根本の関節に相当する肩の位置の投擲中の軌跡を図6右に示した.

ハンマーの加速の基本2:スイング運動
ここでは,さらにハンマーをさらに効率よく加速するための,「スイング運動(振り子運動)による加速方法」について述べていく.
前節で述べたように,ワイヤ軸に作用する張力の主体は向心力で,張力(向心力)と同じ方向に引っ張ることでハンマーを加速していることを説明した.
この加速原理に従いワイヤ軸方向の力学だけを考えれば,ハンマーと腕は一直線のままでもよく,身体はハンマーと綱引き状態で回転し続ければよいことになる.しかし,向心力はハンマーの角速度(回転速度)の大きさの2乗に比例するので,前節で述べた方法のようにローポイントでできるだけ大きな向心力をつくりだすために,両足期のフェーズで,ハンマーの角速度を事前に加速しておくことが重要である.このためにハンマーを腕に対して振動させて角速度を増大させている.
そこで以下では,ハンマーの角速度を増加させるための,接線(回転)方向の力学について述べる.

ここでハンマーは,単振り子のようにハンマーヘッドに質量が集中した質点と,質量を無視したワイヤーで構成された振り子から構成されるとみなす.単振り子の場合,回転中心が固定されているが,ハンマーの場合,ハンドルとワイヤの接合部を回転中心とみなすと,図7のようにハンドル部分にハンマーヘッドの回転方向とは反対方向に加速度(赤色の矢印)を与えることで,ハンマーの角速度を増加させられる.なお,この加速原理の物理的な説明は補足2で行う.

そのハンドル部分には,主として腕の回転による向心加速度が図8右の黒い矢印の方向に作用し,ハンマーと同様に腕も高速に回転しているので,ハンドル部の加速度では非常に大きなこの向心加速度が占めている.
そこで,肝心の反対方向の接線加速度を作り出すために,まず両腕も一つの振り子とみなした「腕」の振り子をハンマーの回転方向と同じ方向に加速度を与えることで(図8参照),ハンマーがわずかばかり腕に対して遅れて回転させ,これにより腕とハンマー間に相対角をつくり,ハンドル部分の加速度(黒)のうち接線方向の加速度(赤)を発生させることができる.この結果,ハンマーの角速度を増大させている.相対角はわずか10〜20deg 程度であるが,腕も高速に回転することで腕の向心加速度もかなり大きくなるため,接線方向の加速度成分も十分な大きさとなる.
こうして獲得した接線加速度によって,ハンマーの角速度は増大している.なお,このような腕の回転による加速は両足期に可能で,片足期にはハンマーの角速度を増やすことは難しい.
また,このようなスイング運動による回転の加速は,バットスイングややゴルフスイングでも同様な方法に基づいている.ゴルフスイングについては別章で取り上げる予定である.
ハンマーの加速方法のまとめ
ハンマー投の加速は主としてワイヤ軸方向とそれに直交する回転(接線)方向の力学によって,加速方法が分かれる.
両足期の前半には(ローポイント付近まで)スイング運動によって角速度を増加させ,それにともない回転の運動エネルギーを増加させることで大きな向心力を獲得する.その後その向心力が最大化したローポイント付近で,その向心力と同じ方向(ワイヤ軸方向)に引っ張ることで,さらにハンマーの力学的エネルギーを増加させている.
なお,図8のような二重振り子モデルを考えたときに,ハンマーに作用する張力は前章で述べた内力に相当する.ハンマーの加減速は全て内力を媒介した腕とハンマー間のエネルギー伝達によって行われているのが,ハンマー投の特徴である.
前章で内力が関節を介してエネルギー伝達に寄与し,内力によるエネルギー伝達が運動パターン形成に寄与していることを述べた.ハンマー投では内力を媒介したエネルギー伝達が,「スイング運動」と「引っ張り運動」という運動パターンの形成を行っている.
また,ここで述べた二重振り子のシステムは劣駆動系で,ハンマーと腕間の関節にはアクチュエータ(筋肉による動力源)が存在しない.にもかかわらず,以降の章で説明するゴルフスイングなどと同じ原理でスイング運動を行い加速していることから,関節における筋肉の有無に関わらず,「内力を媒介したエネルギー伝達がスイング運動という基本的な運動パターンを形成している」ことを示唆している.すなわち,筋肉は内力によるエネルギー伝達による運動パターン形成と協調するように作用することで,エネルギー消費を抑えながら効率よく運動していることが推察される.
また,このような運動の特徴がスポーツだけに当てはまるのか,それとも我々の日常の運でも当てはまるのかということも気になるところである.
補足
ここでは「3次元空間における二重振り子モデル」によるハンマー投の加速方法の数理について説明を行う.読み飛ばしていただいて結構だが,力学に関心のある方は参考にしていただき,最後の動画はご覧になっていただければと思う.詳細は参考文献1,2)に示されている.
補足1:ハンマー投の力学(ワイヤ軸方向のダイナミクス)
投擲方向の制御の問題を独立に考えるならば,基本的にはハンマーの運動エネルギーを最大化することが投擲運動の重要な目的となる.そこで前章
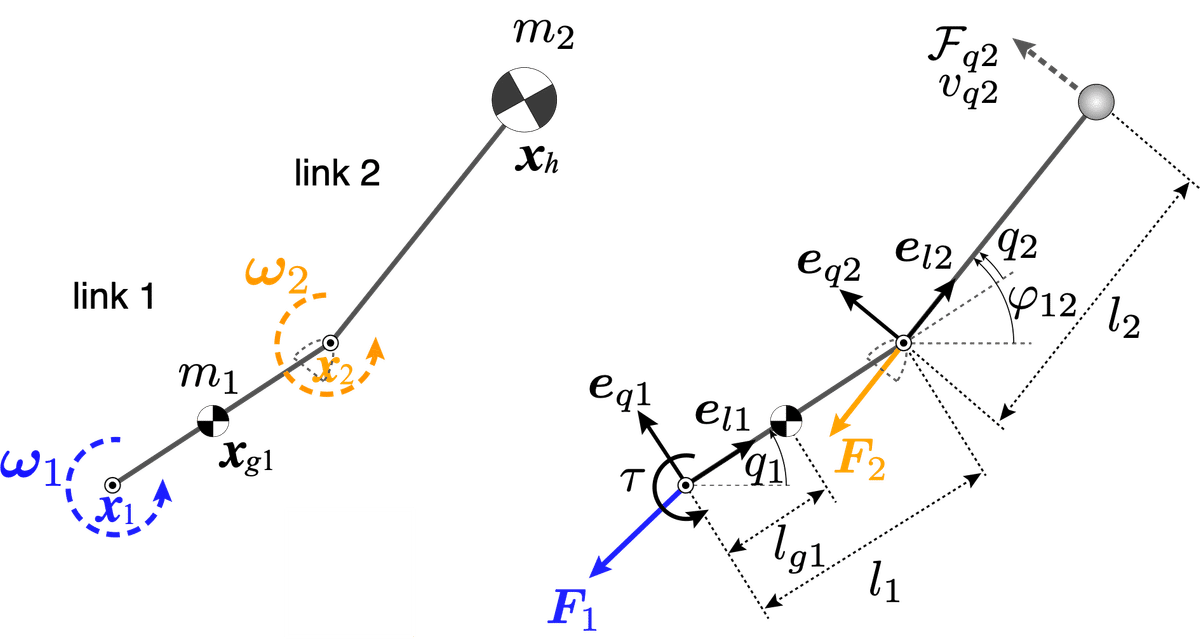
と同様に,ハンマーの力学的エネルギーの変化率を考える.前章の2リンクの剛体モデルでは二つの剛体から構成される「剛体」の二重振り子を考えたが,ここではハンマーヘッドに質量が集中しているとみなし,剛体と質点の振り子から構成される二重振り子を考える(図9,10参照).

ここで,ハンマーの力学的エネルギー$${E_2}$$は
$$
E_2 = \frac{1}{2} m_2 \dot{\bm{x}}_2^T \dot{\bm{x}}_2 - m_2 \bm{g}^T \bm{x}_2
$$
となり,$${m_2}$$はハンマーの質量,$${\bm{x}_2}$$はハンドルの位置ベクトル,$${\bm{g}}$$は重力加速度である.このエネルギーの時間微分$${\dot{E}_2}$$は
$$
\dot{E}_2=F_2 ~v_l
$$
に帰着する.この式の導出は最後の付録2を参照されたい.この式は,ハンマーの力学的エネルギーの変化率がハンマーのハンドル部分に作用する張力$${F_2}$$と,ハンドル部分の速度ベクトル$${\bm{v}}$$のワイヤ軸成分$${v_l}$$との積で決まることを示している(図9参照).すなわち,「1.ハンマーのワイヤーに作用する張力$${(F_2<0)}$$の大きさを増大させ」,「2.ワイヤ軸方向に引っ張り速度$${(v_l <0)}$$を与える」ことによって,ハンマーを加速することができる.
この式からは見かけ上,「ワイヤ軸方向のダイナミクス(力学)」だけでエネルギー変化が決まることを示している.
実際,ハンマーを加速する両足期のローポイントでは,身体全体で綱引きをするように,ワイヤ軸方向にハンマーを引っ張る速度を与えて加速している.そして,ハンマーの速度も,各ローポイント付近で速度が最大になる.
図9のグラフは,張力$${F_2}$$は変動はあるものの向心力のせいで常に負の方向を向き($${F_2<0}$$),ハンドル部分の速度$${v_l}$$は,おおよそ両足期に引っ張ることで張力と同じ負の方向を向き,片足期に入るとハンマー側に逆に引っ張られ($${v_l>0}$$),ハンマーのエネルギーが減少($${F_2 ~v_l < 0}$$)していることを示している.
しかし,ここで重要なことは,両足期に入りハンマーの角速度が増加し,それにともないハンドルに作用する張力$${F_2}$$が向心力の増加にともない増大し,向心力がローポイント付近で最大化することである.
したがって,ハンマーを加速させるためには,ローポイント付近で引っ張るだけではなく,ローポイントを迎えるまでにハンマーの角速度を事前に増大させておくことが重要となる.ワイヤ軸方向のダイナミクスだけがエネルギー増加を決定するのではなく,次のハンマーの回転のダイナミクスの理解も必要となる.
補足2:ハンマーの力学(回転方向のダイナミクス)
ハンマーは,単振り子のように,ハンマーヘッドに質量が集中した質点と,質量を無視したワイヤーで構成された振り子から構成されるが,根元側(リング部分)$${\bm{x}_2}$$を3次元空間で自由に動かせる振り子である(図10参照).

3次元空間でハンマーの自由度は6自由度と考えることもできるが,ここではワイヤを質量がなく伸縮のない糸(線分)とみなし,ハンドルの位置$${\bm{x}_2}$$の3自由度と回転の2自由度を合わせて,実際には5自由度ともいえる.これは,ワイヤ軸回りの回転を定められないため,回転については1自由度,縮退(退化)していると考えている.また,おおよそハンマーと腕から構成される二重振り子も一定の平面内を運動しているとみなせるので,平面内の振り子運動の4自由度とみなすこともできるが,ここでは3次元空間を自由に運動できるモデルを考える.
ハンマーは単振り子と同じ構造で,ハンマーにはワイヤ軸方向($${\bm{e}_{l2}}$$方向)だけに張力$${F_2}$$が作用するため,ハンマーのダイナミクスは
$$
F_2 = m_2 \bm{e}_{l2}^T \left\{\ddot{\bm{x}}_2 -\bm{g} \right\} + m_2 l_2 \bm{\omega}_2 \times (\bm{\omega}_2 \times \bm{e}_{l2})
$$
と書ける(導出は付録1参照).ここで,右辺の第1項はハンドル部分の加速度$${\ddot{\bm{x}}_2}$$と重力加速度$${\bm{g}}$$のワイヤ軸方向($${\bm{e}_{l2}}$$)成分であり,第2項はハンマーの角速度$${\bm{\omega}_2}$$で定まる向心力で$${-\bm{e}_{l2}}$$方向に作用し,張力$${F_2}$$はハンマーの角速度に依存することを示している.
次にこの向心力が,どのように定まるか考えていく.
ハンマーの回転の力学
前述のように,ハンマーにはワイヤ軸方向に張力しか作用しないため,それに直交する方向には力が作用しないが,角速度を決めるのは接線(回転)方向のダイナミクスであるので,向心力を増加させるメカニズムを回転のダイナミクスに基づいて考える.図10の二重振り子モデルのハンマーの回転のダイナミクスは
$$
m_2 l_2 \dot{\bm{\omega}}_{2} \times \bm{e}_{l2} = -m_2 \bm{e}_{q2}^T (\ddot{\bm{x}}_2 - \bm{g})
$$
となる(導出は付録1を参照).左辺はハンマーの角加速度に関する項で,右辺はハンドル部分の加速度$${\ddot{\bm{x}}_2}$$と重力加速度$${\bm{g}}$$の,回転方向とは反対方向成分$${-\bm{e}_{q2}^T (\ddot{\bm{x}}_2-\bm{g})}$$で決まることを示している.
ハンマーに作用する張力を増大させるためには,角速度を大きくして向心力を増大させる必要があるが(左辺の意味),そのためにはハンマーのハンドル部分$${\bm{x}_2}$$で「回転方向とは反対方向$${- \bm{e}_{q2}}$$の加速度$${- \bm{e}_{q2}^T \ddot{\bm{x}}_2}$$(図8の赤色の矢印に相当)」を増やす必要があることを示している(右辺の意味).
ここで,ハンドル部分の加速度$${\ddot{\bm{x}}_2}$$は,
$$
\ddot{\bm{x}}_2 = \ddot{\bm{x}}_1 + l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1})
$$
と書けるので,回転のダイナミクスは
$$
m_2 l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2} = -m_2 \bm{e}_{q2}^T (\ddot{\bm{x}}_2 - \bm{g}) \\= -m_2 \bm{e}_{q2}^T (\ddot{\bm{x}}_1 + l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1}) - \bm{g})
$$
のように書き替えることができる.
ここで,$${\bm{x}_1}$$は肩の位置ベクトル,$${\bm{\omega}_1}$$は肩の角速度ベクトル,$${\bm{e}_{l1}}$$は腕の振り子の軸に沿った単位ベクトルである.
すなわち「回転の反対方向$${- \bm{e}_{q2}}$$の加速度$${- \bm{e}_{q2}^T \ddot{\bm{x}}_2}$$」を
$${- \bm{e}_{q2}^T \left(\ddot{\bm{x}}_1 + l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1})\right)}$$
に置き換えたわけだが,この中で,腕の向心力の項$${l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1})}$$の接線方向成分が支配的で,図6の接線加速度成分として,ハンマーの角速度増大に最も貢献している.
補足3:ハンマーのエネルギー変化率
ここでは前章と同様に,ハンマーの力学的エネルギーの時間変化から,ハンマーの加速メカニズムを考える.
補足1で示したように,ハンマーの力学的エネルギーの時間変化は$${\dot{E}_2=F_2 ~v_l}$$に帰着し,「ハンマーの加速の基本1:パラメータ励振」節では,この原理に基づいて,ブランコの加速と同様なパラメータ励振によってハンマーを加速する方法について述べた.すなわち,ハンマーの作用する張力$${F_2}$$が最大になるローポイントで,速度$${v_l=\bm{e}_{l2}^T \dot{\bm{x}}_2}$$でワイヤ軸方向に引っ張ることでエネルギーを増大させることでハンマーを加速させることができる(図11左参照).

また「ハンマーの加速の基本2:スイング運動」節では,その効果を最大化するため張力$${F_2}$$を大きくすることが課題となり,その張力の大半を占めるハンマーの向心力が,ハンマーの角速度$${\bm{\omega}_2}$$の大きさの2乗に比例しているため,引っ張る前にハンマーの角速度の増加させることが重要であることを述べた(図11右参照).
そのハンマーの角速度増加のためには,ハンドル部分の接線加速度をハンマーの回転方向とは反対方向に増やす必要がある.
そこでここでは,エネルギー変化率の議論によって,この角速度増大方法について考えていく.
繰り返しになるが,補足1で示したように,ハンマーの力学的エネルギーの時間変化は$${\dot{E}_2=F_2 ~v_l}$$に帰着する.そこで,ここではハンマーの回転の運動エネルギーを考え,その微分によって角速度増化メカニズムを考察する.
なお,ハンマーは基本的には質点運動であるが,単振り子のように回転のダイナミクスから「仮想的」に回転の運動エネルギー$${\mathcal{E}_{q2}}$$を以下のように定義する.
$$
\mathcal{E}_{q2} = \frac{1}{2} \bm{\omega}_2^T \bm{J}_2 \bm{\omega}_2 \\ = \frac{1}{2} [\omega_{2x}~\omega_{2y}~0]\begin{bmatrix}m_2 l_2^2 & 0 & 0 \\ 0 & m_2 l_2^2 & 0 \\ 0&0&0\end{bmatrix} \begin{bmatrix}\omega_{2x} \\ \omega_{2y} \\ 0\end{bmatrix} \\ = \frac{1}{2} m_2 l_2^2\left(\omega_{2x}^2 + \omega_{2y}^2\right)
$$
ここで,$${\bm{\omega}_2=[\omega_{2x}~\omega_{2y}~0]^T}$$はハンマーの角速度で,ワイヤ軸方向を$${z}$$方向としたときに,軸回りの角速度を0とし,$${\bm{J}_2}$$はハンドル部分$${\bm{x}_2}$$を原点としたハンマーの慣性モーメントテンソルで,角速度と同様にワイヤ軸,すなわち$${z}$$軸回りの慣性モーメントを0とした.
なお,この回転の運動エネルギー$${\mathcal{E}_{q2}}$$は,ハンマーの運動エネルギー$${\frac{1}{2}m_2 \dot{\bm{x}_2}^T \dot{\bm{x}_2}}$$のうち,その接線成分を意味している.
そこでいつものように,$${\mathcal{E}_{q2} }$$の時間微分を計算すると,
$$
\dot{\mathcal{E}}_{q2} = \mathcal{F}_{q2}^T \bm{v}_{q2}
$$
となる.ここで,$${\mathcal{F}_{q2}}$$はハンマーの回転の接線方向の加速力ベクトル,$${\bm{v}_{q2}}$$は接線方向の速度ベクトルで(図10参照),
$$
\mathcal{F}_{q2} = m_2 l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2}
$$
$$
\bm{v}_{q2} = \bm{\omega}_2 \times \bm{e}_{l2}
$$
と表され,力と速度の両方ともワイヤ軸方向$${\bm{e}_{l2}}$$に直交し,回転の接線方向を向いている.回転の運動エネルギーの時間微分も,回転(接線)方向の加速力と接線方向の速度との積に帰着する.
次に投擲時の$${\mathcal{F}_{q2}}$$と$${\bm{v}_{q2}}$$の変化を図12(b)に示す.図12(a)は図9と同じグラフで,ワイヤ軸方向に作用する力$${F_2}$$とワイヤ軸方向の速度$${v_l}$$の変化を示している.
接線方向ではワイヤ軸方向と反対に,速度が常に正($${v_{q2}>0}$$)で,力$${\mathcal{F}_{q2}}$$の符号が入れ替わり,主として両足期に正となる.

図12(c)にワイヤ軸方向のエネルギー変化率と回転方向のエネルギー変化率を比較した.回転方向のエネルギーは両足期の前半で増加し(破線),その後,ハンマーの引っ張り運動でさらにエネルギーを増加させている.
このことは,この節の冒頭で述べたように,両足期の前半に(ローポイント付近まで)スイング運動によって角速度を増加させ,すなわち回転の運動エネルギーを増加させることで向心力を増加させ,向心力が最大化するローポイント付近でその向心力と同じ方向に引っ張ることで,さらにハンマーの力学的エネルギーを増加している戦略を示している.
グラフで示してもなかなか分かりづらいかもしれない.そこで下記動画は,これらのエネルギー変化率の解析をまとめた動画である.動画の左下の矢印は投擲方向を示している.下(手前)側がローポイントである.ワイヤ軸方向の矢印は(水色)$${\dot{E}_2}$$に相当し,内側に向いているときはエネルギーが増加し,外側に向いているときに減少していることを意味する.また矢印の長さはハンマーの力学的エネルギーの変化率$${\dot{E}_2}$$の大きさを表している.
ピンク色の矢印は回転方向のエネルギー変化率$${\mathcal{E}_{q2}}$$を表し,回転方向を向いているときにその増加を,反対方向は減少を表し,同様に矢印の長さがハンマーの回転のエネルギー変化率$${\mathcal{E}_{q2}}$$の大きさを示している.
各回転毎に,ローポイントを時計の6時と定めると,おおよそ10時ぐらいから回転のエネルギーを増大させて向心力を増やし,ローポイント(6時)で牽引動作によってハンマーの力学的エネルギーが増大している様子が動画からもわかる.また4時ぐらいを過ぎると,エネルギーが減少し始めるが,特に水色の力学的エネルギー変化の矢印の長さを比較すると両足期で増大する量と片足期で減少する量に違いがあり,全体的には加速方向に向かっている様子も観察できる.
付録
付録1:ハンマーと腕の運動方程式
図8などに示したように,両腕を一つの剛体とみなし,ハンマーは単振り子のように質量がハンマーヘッドに集中した振り子とみなし,これらの二つの振り子から構成される二重振り子を考える.
ハンマーヘッドの位置ベクトル$${\bm{x}_h}$$は
$$
\bm{x}_h=\bm{x}_2+ l_2 \bm{e}_{l2}\\ = \bm{x}_1+l_1 \bm{e}_{l1} + l_2 \bm{e}_{l2}
$$
と表される.ここで,$${\bm{x}_1, \bm{x}_2}$$は肩の中心(腕の関節)と,ハンドルの位置ベクトル,$${\bm{e}_{l1}, \bm{e}_{l2}}$$は腕とハンマーの軸方向の単位ベクトル,$${l_1, l_2}$$は各振り子の長さである.
この$${\bm{x}_h}$$を微分することで,次のようにハンマーヘッドの速度
$$
\dot{\bm{x}}_h = \dot{\bm{x}}_2+ l_2 \bm{\omega}_2 \times \bm{e}_{l2} \\=\dot{\bm{x}}_1+l_1 \bm{\omega}_1 \times \bm{e}_{l1} + l_2 \bm{\omega}_2 \times \bm{e}_{l2}
$$
と加速度
$$
\ddot{\bm{x}}_h =\ddot{\bm{x}}_2 + l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2}+ l_2 \bm{\omega}_2 \times (\bm{\omega}_2 \times \bm{e}_{l2}) \\=\ddot{\bm{x}}_1+l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1}) + l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2}+ l_2 \bm{\omega}_2 \times (\bm{\omega}_2 \times \bm{e}_{l2})
$$
を得る.ここで,$${\bm{\omega}_1, \bm{\omega}_2}$$は腕とハンマーの角速度ベクトルである.
ハンマーヘッドには張力$${F_2}$$と重力が作用し,ハンマーの運動方程式は,
$$
m_2 \ddot{\bm{x}}_h = -F_2 \bm{e}_{l2} + m_2 \bm{g}
$$
となる.
この運動方程式に,先程のハンマーヘッドの加速度$${\ddot{\bm{x}}_h}$$を代入することで,またハンマーにはワイヤ軸方向に張力$${F_2}$$しか作用しないので,ワイヤ軸方向のダイナミクス
$$
F_{2} + m_2 \bm{e}_{l2}^T \bm{g}=m_2 \bm{e}_{l2}^T \left\{\ddot{\bm{x}}_2 + l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2}+ l_2 \bm{\omega}_2 \times (\bm{\omega}_2 \times \bm{e}_{l2}) \right\} \\ F_2 = m_2 \bm{e}_{l2}^T \left\{\ddot{\bm{x}}_2 -\bm{g} \right\} + m_2 l_2 \bm{\omega}_2 \times (\bm{\omega}_2 \times \bm{e}_{l2})
$$
となる.なお,ハンマーは単振り子構造を持ち,剛体ではなく線分とみなせるため,ワイヤ回りの角速度を零としたハンマーの角速度ベクトルを$${\bm{\omega}_2}$$と定める.また,二重振り子の根元側の振り子は,両腕から構成される一つの剛体振り子とした.そして,角速度ベクトル$${\bm{\omega}_2}$$とワイヤ軸に垂直な方向の単位ベクトルを$${\bm{e}_{q2}}$$と定め,ワイヤ軸に垂直な方向$${\bm{e}_{q2}}$$のハンマーの加速度は
$$
\bm{e}_{q2}^T \ddot{\bm{x}}_h=\bm{e}_{q2}^T \left\{\ddot{\bm{x}}_1+l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1}) + l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2}+ l_2 \bm{\omega}_2 \times (\bm{\omega}_2 \times \bm{e}_{l2}) \right\} \\= \bm{e}_{q2}^T \left\{\ddot{\bm{x}}_1+l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1})\right\} + l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2} \\= \bm{e}_{q2}^T \ddot{\bm{x}}_2 + l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2}
$$
のように定まり,接線方向$${\bm{e}_{q2}}$$のダイナミクス,すなわちハンマーの回転のダイナミクス
$$
m_2 \bm{e}_{q2}^T \left\{\ddot{\bm{x}}_1+l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_{l1})\right\} + l_2 m_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2} = m_2 \bm{e}_{q2}^T \bm{g}\\ m_2 l_2 \dot{\bm{\omega}}_2 \times \bm{e}_{l2} = -m_2 \bm{e}_{q2}^T \left\{(\ddot{\bm{x}}_1 - \bm{g})+l_1 \dot{\bm{\omega}}_1 \times \bm{e}_{l1} + l_1 \bm{\omega}_1 \times (\bm{\omega}_1 \times \bm{e}_1)\right\} \\ = -m_2 \bm{e}_{q2}^T (\ddot{\bm{x}}_2 - \bm{g})
$$
を得る.
付録2:ハンマーのエネルギー変化率
ハンマーの力学的エネルギーは
$$
E_2=\frac{1}{2}m \dot{\bm{x}}_h^T \dot{\bm{x}}_h - m \bm{g}^T \bm{x}_h
$$
となり,これらの時間微分は,付録1のハンマーの運動方程式と,張力$${F_2}$$がワイヤ軸方向$${\bm{e}_{l2}}$$方向にしか作用しないことを利用し,
$$
\dot{E}_2=m \ddot{\bm{x}}_h^T \dot{\bm{x}}_h - m \bm{g}^T \dot{\bm{x}}_h\\=m(\ddot{\bm{x}}_h - \bm{g})^T \dot{\bm{x}}_h\\=\bm{F}_2^T \dot{\bm{x}}_h\\=F_2 \bm{e}_{l2}^T \dot{\bm{x}}_h\\ = F_2 \bm{e}_{l2}^T \dot{\bm{x}}_h \\ = F_2 \bm{e}_{l2}^T (\dot{\bm{x}}_2+ l_2 \bm{\omega}_2 \times \bm{e}_{l2}) \\ = F_2 \bm{e}_{l2}^T (\dot{\bm{x}}_2) \\=F_2 v_l
$$
を得る.
参考文献
1)二重振子のパラメータ励振原理によるハンマー投運動の数理解析 ,太田,梅垣,室伏,羅,日本機械学会シンポジウム:スポーツ・アンド・ヒューマンダイナミクス講演論文集,pp.319-324,2010
2)ハンマー投のダイナミクスに基づくサイバネティック・トレーニング ,太田,梅垣,室伏,羅,バイオメカニクス研究,Vol.17,No.1,pp.26-36,2013


【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
