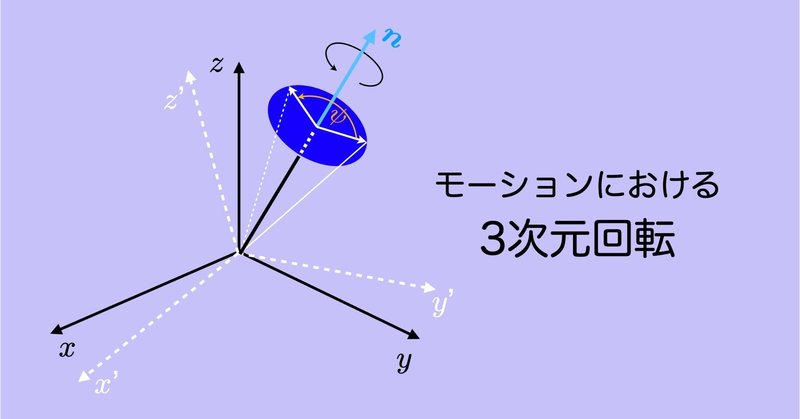
運動計測では,3次元回転に関する数学的理解が不可欠です.しかし,バイオメカニクスの教科書には詳しい解説は見当たりません.単位クォータニオンを中心に他の分野でも書かれていないことも…
- 運営しているクリエイター
#方向余弦
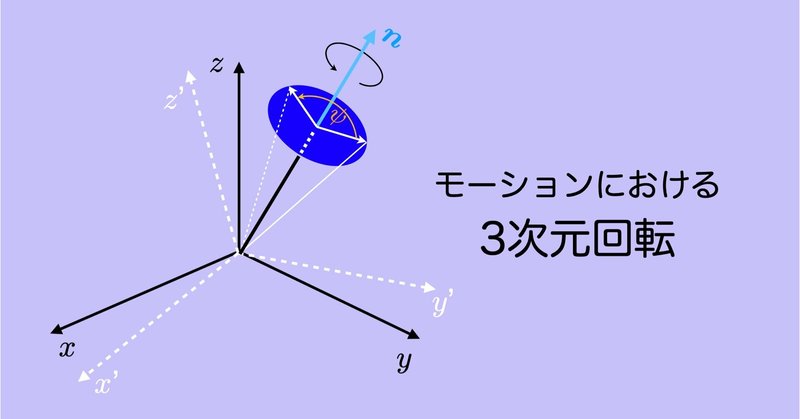
モーションにおける3次元回転 #10 〜平面角度の計算〜
バイオメカニクスの解析では身体や剛体の3次元回転の解析を行うよりも,「内外転角」や「回旋角」などの1自由度の回転角を解析することのほうが多いかもしれない.この1自由度の角度は平面内で記述される角度で,例えば,直線間のなす角度は2直線が形成する平面内の角度であり,直線と平面のなす角度は直線と平面が構成する面内の角度であり,回旋角度は回旋軸に垂直な面内の角度である.このように,ここでは平面内の1軸回転
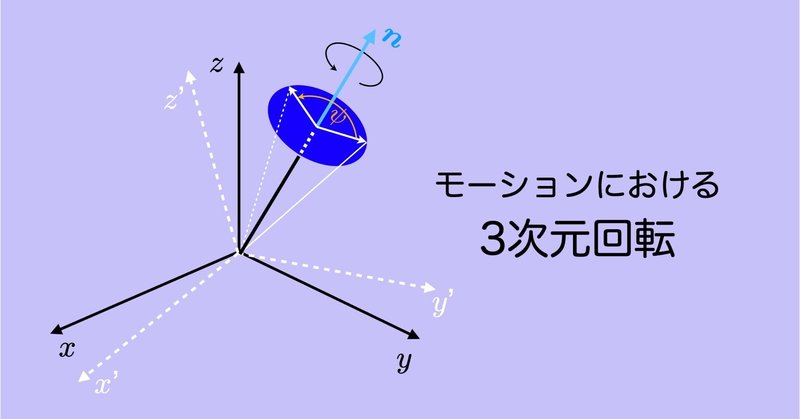
もっとみるモーションにおける3次元回転 #2 〜方向余弦行列としての回転行列〜
前章「モーションにおける3次元回転 #1 」で方向余弦行列について触れたが,モーションキャプチャで回転行列を計算する際,多くの場合,方向余弦行列を算出することになるため,ここで少し方向余弦について補足しておく.
前章では,正規直交基底とは直交する座標系の各軸に固定された3つの単位ベクトルで,回転行列はこの正規直交基底を並べたものであることを述べた(図1).
図1の場合,直交する座標系の各$${X
モーションにおける3次元回転 #1
はじめに
バイオメカニクスの解析では,たとえば「腕と地面のなす角度」「腕の回旋角度」を算出するなど多種多様な解析が必要とされ,問題に応じて自分で解析方法を考えなくてはいけないことが多い.
また,モーションキャプチャなどで関節点の3次元位置が得られているなら,比較的これらの計算は容易であるが,モーションセンサ(IMU)でクォータニオンが出力され,そこからセンサの傾き角度をどのように算出するかとな