【解説】小学生でも答えられる１問。論理的に証明できますか？｜一橋大学1973年数学

こんにちは、数学講師ごとうです。昨日は国公立大学の前期試験の合格発表でしたね。合格した皆さん、本当におめでとうございます。後期試験のある皆さん、引き続き頑張っていきましょう。

今日は【論理的に証明すること】の難しさと面白さを体現している問題を紹介したいと思います。少し古い問題になってしまい恐縮なのですが、1973年の一橋大学の前期試験の数学です。

問題

平面内で４つの正方形の辺を重ねてできる図形は何種類か。ただし、同一平面内で回転して重なるものは同じとみなす。

（1973年一橋大学 前期試験 数学）

※問題文は分かりやすく改変しています。

頑張って数えればわかる

問題の条件を満たす図形の例として思いつくのは

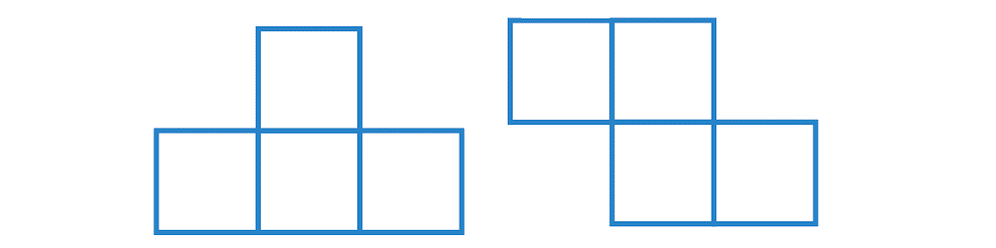
のようなものがあります。これを見た人はTETRISを思い出すかもしれませんね。実際、この問題の答えは、TETRISで登場するブロックの種類と同じ７種類です。（この出題は1973年、TETRISが世に出てきたのは1984年ですので関係はないですが‥。）ここまでは頑張って数えればわかりますし、小学生でも解けてしまいそうな問題に感じます。

しかし、数学では「解答した図形の種類以外の解は絶対に存在しない」ことを論理的に証明する必要があります。難しいことですが、僕はここに面白さも感じます。

みなさんならどのように答えますか？

解説

「解答した図形の種類以外の解は絶対に存在しない」ことを論理的に証明する方法として、正方形の直線上の連結数が最大でいくつになっているかで場合分けをする方法があります。具体的に考えてみましょう。

まず、正方形の数は４つなので、どんなに多くても連結数が５以上になることはありません。また、正方形をつないだ時点で必ず連結数は２以上になるので、連結数が１以下になることもありません。ここまで述べたうえで、以下のように場合分けします。

①連結数が最大で４のときは
□□□□
の１種類しかありえません。

②連結数が最大で３のときは、□□□まで作成してから考えます。

下図において、Ａに正方形を連結すると、最大連結数が３を超えてしまう（パターン①になる）ので新たな連結が許されるのはそれ以外の６箇所です。では、Ｂ・Ｃ・Ｄにそれぞれ正方形を連結すると、３種類が得られます。

※ＡからＤがそれぞれ２か所あるのは、同一平面内で180℃回転すると重ねられるためです。

③連結数が最大２のとき、□□までとりあえず作成してみましょう。

次に、残り２つ残る□のうち、１つ目の□をどこに配置するかを考えましょう。最大連結数が３にならないように（②のパターンにならないように）連結できる場所は４か所あります。しかし、どこに連結しても図形全体を回転させることで結局のところ下図のようになります。

では最後の□を連結する場所を考えましょう。

これまでと同様に、Ａに連結すると最大連結数が２を超えてしまうので不適切です。また、残りのＢ・Ｃ・Ｄに連結してできる新しい３種類の図形は同一平面内で回転させても互いに重なることはありません。

以上より、題意を満たす図形は全部で７種類あることが分かりました。

今回の問題においては、「求めた解以外は存在しない」ことを論理的に解くことの大切さが分かります。

「答えが７種類である」ことが大事なのではありません。「どうして７種類なのか」を考えられることが大事なのです。

こうした考え方ができる生徒たちを増やしていけるように、今日からも頑張っていきたいと思います。

.

■自己紹介

■国公立大学の数学問題を、思考法を含めて解説しています。

国公立大学 数学問題の解説｜数学講師ごとう｜45日で京大合格・逆転合格｜note