
【コラム】組み合わせの計算nCrを使いこなす(Part1)
今回と次回の2回にわたって、場合の数で学ぶ演算子「nCr」に注目してみたいと思います。
もともとこの記号は次のように定義されています。
n個の異なるものからr個取り出すときの方法の数
この定義に基づいて数式の意味を考えてみると、様々な等式が
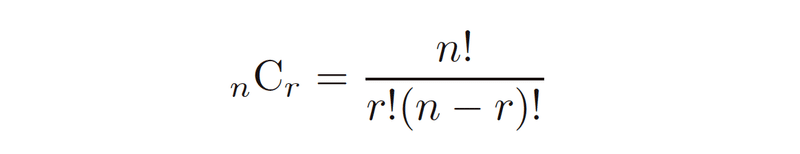
を用いた計算をすることなく証明できます。
ウォーミングアップ
まずはウォーミングとしてこの等式の意味を考えてみます。
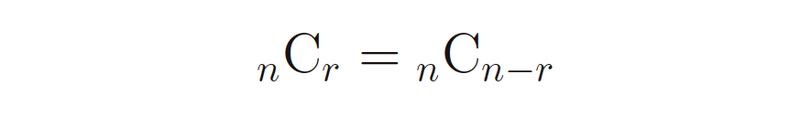
左辺は定義どおり
n個の異なるものからr個を取り出すときの方法の数
と捉えることとしましょう。しかし、右辺も定義通りに
n個の異なるものから(nーr)個を取り出すときの方法の数
と捉えてしまうと、左辺と右辺が同じものであるとはちょっと言えませんね。
ここは右辺を
n個の異なるものから、取り出さない(nーr)個のものを選ぶ方法の数
と考えてみることとします。そうすると、これは「n個の異なるものからr個のものを取り出す方法の数」であるとも言えるので、左辺が表す意味に一致します。
パスカルの三角形
次はパスカルの三角形で有名な等式です。パスカルの三角形において、隣り合う2つの項の和は下段の間の数に一致するという法則がありましたね。
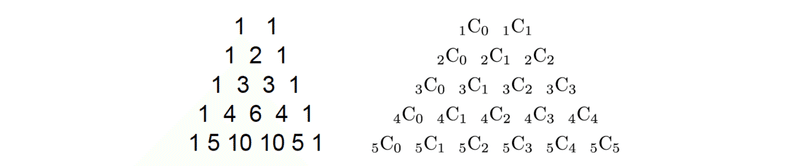
これ↑です。今回も左辺を定義どおり
(n+1)個の異なるものから(r+1)個取り出すときの方法の数
と捉えることとします。一方で、右辺がどのようにして左辺に一致するのか簡単には分かりません。
そこで、右辺が2つの項の和の形をしていることに注目して、左辺が表すものを互いに排反かつすべての場合を含む2つの事象として分離できないか、考えてみましょう。
まず最初に、左辺の解釈にある「(n+1)個の異なるもの」の中の(どれでも良いので)1つを特別扱いし、Xと名付けることにします。
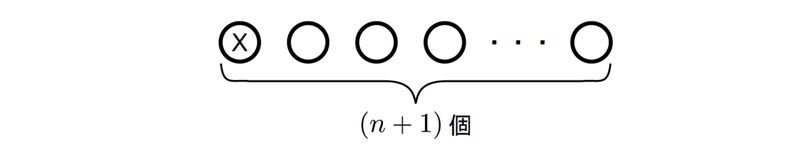
右辺の3つの項はそれぞれこのXを取り出す場合と取り出さない場合として考えてみると上手くいきます。即ち、1 つ目の項は「Xは取り出した上で、残りのn個からr個取り出すときの方法の数」となります。
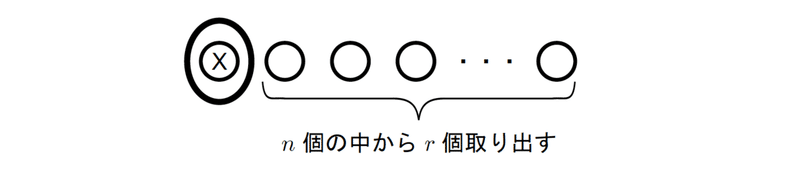
そして2つ目の項は「Xは取り出さないで、残りのn個から(r+1)個取り出すときの方法の数」となります。
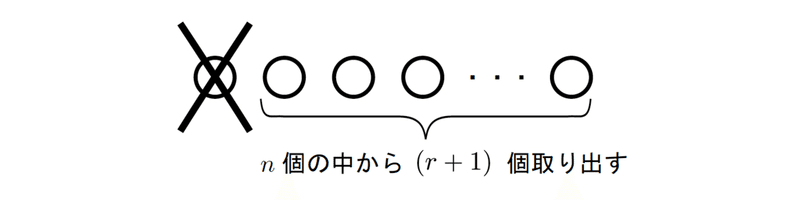
と捉えれば良いのです。Xを取り出す場合と取り出さない場合は互いに排反かつ全ての場合を含んでいるので、確かに左辺が表していた(n+1)個の異なるものから(r+1)個を取り出す方法の数になっています。
以上のように数式の意味を考えるだけで解ける問題は意外なほどに多いです。次回はnCrに関するもう少し発展的な等式を見ていきます。
.
■自己紹介
■国公立大学の数学問題を、思考法を含めて解説しています。
■受験勉強に役立つ、数学コラムを投稿しています。
この記事が気に入ったらサポートをしてみませんか?
